Overview
资料来源: 里卡多梅希亚-阿尔瓦雷斯, Hussam Hikmat 贾巴尔和艾哈迈德·阿卜杜勒拉蒂夫, 密歇根州立大学机械工程系, 东兰辛, MI
由于其治理规律的非线性性质, 流体运动诱发了复杂的流型。几个世纪以来, 对这些模式的本质的了解一直是人们密切关注的课题。虽然个人电脑和超级计算机广泛用于推断流体流动模式, 但它们的能力仍然不足以确定复杂几何形状或高度惯性流的精确流动行为 (例如, 当动量支配粘性阻力)。考虑到这一点, 大量的实验技术, 使流模式明显的发展, 可以达到流的制度和几何无法进入理论和计算工具。
这个演示将调查一个钝体周围的流体流动。一个钝体是一个物体, 由于其形状, 导致其表面的分离流动。这是与流线型的身体形成对比, 就像一个翼型, 这是在流中对齐, 导致较少的流分离。本研究的目的是利用氢泡作为一种可视化流动模式的方法。氢泡是通过电解在水中的电极, 利用直流电源产生的。在负极中形成氢气气泡, 这需要是一个非常细的导线, 以确保气泡保持小, 更有效地跟踪流体运动。该方法适用于稳定的层流流动, 并基于描述物体绕流性质的基本流动线。[1-3]
本文重点介绍了该技术的实现, 包括设备及其安装的细节。然后, 该技术用于演示使用两个基本的流动线来表征循环圆柱体周围的流动。这些流动线用于估计一些重要的流量参数, 如流速和雷诺数, 并确定流动模式。
Principles
在这一配置中, 我们将考虑一个均匀的水流速与速度 (称为自由流流速) 接近一个圆柱体 (图 1). 
根据雷诺数所描述的流动条件, 这种流动可能会变得不稳定, 并引起涡脱落。涡脱落是典型的流动过去的钝体, 而不是流线型的机构, 展示边界层分离在他们的表面的大部分。这种边界层分离导致形成的漩涡背后的身体, 可能最终分离到尾迹。当周期性的分离发生时, 当脱落频率与身体的固有频率重合时, 涡产生在机体后面的低压交替区域, 这可能成为共振载荷。这个旋涡脱落过程被称为 "冯 Kármàn 涡街" (图 2)。这种旋涡涡旋的重复模式是由钝体周围的非恒定流分离引起的, 并发生在雷诺数的一定范围内。避免这种情况在设计诸如烟囱和桥柱等工程结构中是非常重要的, 因为它可能导致灾难性的失败。
图1.流过圆柱。基本配置示意图。具有速度的齐次流 
接近直径的直线圆柱形,其对称轴与接近的速度垂直. 
雷诺数是一个无量纲参数, 定义为惯性力与粘性力的比值:
(1)
其中, 是流体的运动粘度, 特征速度 (在本例中为), 以及圆柱直径. 
雷诺数可以说是流体流动特性中最重要的参数, 在目前的实验中将被用作 Kármàn 涡街出现的量度。特别是当雷诺数在5左右时, 流在气缸后面有两个稳定的反旋转涡旋。随着雷诺数的增加, 这两个涡旋沿流动方向拉长。当雷诺数达到大约37的值时, 由于压力和动量之间的不平衡, 尾迹变得不稳定并开始振荡正弦。雷诺数的进一步增加到47导致二个逆旋转旋涡从圆筒分离在跟随正弦苏醒振荡的交替的序列 [45, 6]。
旋涡从气缸流出的频率不是恒定的;它随雷诺数的值而变化。脱落频率的特点是两相数, 这是另一个无量纲参数的相关性在这个特殊的流体流动配置:
(2)
这里, 是旋涡脱落频率, 长度和速度尺度与雷诺数相同. 
涡脱落频率可以然后描绘为两相数字作为线性函数的反平方根雷诺数 [7]:
(3)
这一函数并不总是单调的, 它表现出进一步的过渡, 由于二次不稳定性欠的流体流动的非线性。因此, 系数和将根据雷诺数范围更改. 
表1显示了这些系数对于在文献 [7] 中被很好地描述的流动制度的价值。
在目前的实验中, 我们将使用流动线来研究圆柱体周围的外部流动。这些流线定义如下:
· Pathline: 流体颗粒随水流移动而随之而来的路径。
· Streakline: 在同一空间位置的所有流体粒子的连续轨迹。
·时间轴: 在形成连续轨迹的同时, 在同一时刻标记的流体粒子集。
·流线: 在瞬间与速度场相切的连续线。
前三行相对容易生成实验, 而流线仅仅是一个数学概念, 一般必须通过后处理的速度场的瞬时捕获。虽然这始终是正确的, 但由于 pathlines、streaklines 和流线是相互重合的, 因此该分析在稳定流中大大简化。相反, 在非恒定流中, 这些线通常不重合。这项技术的实施通常是简单的, 只需要低成本的设备, 而不是更复杂和昂贵的技术, 如粒子图像测速 [1], 粒子跟踪测速 [89], 和分子标记测速仪 [10]。
图2.代表性的结果。(a) 连续的氢泡, 显示 streaklines 的上游扰动。由连杆投射的阴影用于确定从机器到实际单位的转换。还说明了旋涡脱落循环, 以帮助确定适当的脱落频率。(B) 由氢气气泡产生的时间线。由于时间线频率是很好定义的, 可以用来准确地测量流速;计算红线所包含的时间线将用于此估计.请单击此处查看此图的较大版本.
Table1.系数 
和 
的值不同的雷诺数间隔 (从 [8]).
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. 生产连续气泡板:
- 根据图 3中显示的电路图设置设备。
- 在测试部分的下游端固定水中的正极 (参见图 4以供参考)。
- 在流到达研究对象之前, 将负电极固定在上游和靠近感兴趣点的位置, 将气泡释放到流中 (参见图 4以供参考)。水完成了两个电极之间的电路。
- 打开流程设备
- 将频率控制器的拨号设置为位置2。这将建立一个大约 9x10-4 m3/秒的流率。
- 打开直流电源, 将电压提高到大约25伏, 电流将会自行设置190毫安左右。
- 将信号发生器中的波形设置为方形波形 (符号:).
这产生一个0伏-5 v 平方信号, 激活固态继电器 (关闭电路) 在其高位置, 并打开它在低位置 - 对于这个特殊情况, 方波的频率并不重要。它只需要是非零。
- 在信号发生器中最大化 DC 偏移 (+ 5 V)。通过这种设置, 电路总是闭合的, 系统会连续生成气泡。
这产生一个0伏-5 v 平方信号, 激活固态继电器 (关闭电路) 在其高位置, 并打开它在低位置
图3。连接关系图。
图4。测试部分。流从左向右。负电极产生一层氢泡, 并随流动而被冲走。正极被设置在测试部分的下游端, 以避免其扰动。请单击此处查看此图的较大版本.
2. 制作时间表:
- 打开流程设备
- 将频率控制器的拨号设置为位置2。这将建立一个大约 9x10-4 m3/秒的流率。
- 打开直流电源, 将电压提高到大约25伏, 电流将会自行设置190毫安左右。
- 将信号发生器中的波形设置为方形波形 (符号:). 这产生一个0伏-5 v 平方信号, 激活固态继电器 (关闭电路) 在其高位置, 并停用它 (打开电路) 在低位置
- 将信号发生器中的 DC 偏移量设置为 +1 v。
- 将信号发生器中方波的频率设置为10赫兹。
- 将方波的对称性设置为轻微的负 (-2), 以增加时间线之间的空间, 同时保存正确的频率。
3. 使用流动线研究冯 Kármàn 漩涡街道:
- 使用卡尺测量标尺的直径,.
使用 s.i 单位进行此测量 (m)。 - 在负极的下游固定一个圆柱形杆。
- 将高强度放电灯的光投射到氢气气泡层上。确保光线不直接落在视线的后面以防止成像系统的会
- 将可视化系统与标尺对齐;在某种程度上, 只有圆形的尖端是可见的在前面的摄像头。
- 在可视化窗口和杆的下游添加一个标记, 以使用它作为计算每单位时间涡棚循环的参考。
使用 s.i 单位进行此测量 (m)。4. 通过圆柱体的流量的数据分析:
- 从机组到实际空间单位换算系数的确定:
- 测量气泡片上的标尺所投射的阴影的宽度 (参见图 2 (A) 以供参考)。在杆上采取这种测量, 以避免距离失真。这是在机器单位的杆的直径, (点或像素, 取决于格式)
- 使用以下等式确定从机器单位到真实世界单位的换算系数:
- 测量气泡片上的标尺所投射的阴影的宽度 (参见图 2 (A) 以供参考)。在杆上采取这种测量, 以避免距离失真。这是在机器单位的杆的直径, (点或像素, 取决于格式)
- 流速的测定:
- 在钝体的上游选择一组不失真的时间线。
- 测量机器单位中第一个和最后一个时间线之间的距离, (点或像素).
- 计算组中的时间线数,.
- 记下信号发生器产生的方波信号的频率.
- 确定接近的流速从以下等式:
- 雷诺数的确定:
- 找到工作流体的运动粘度 (例如水 m
2/秒)。 - 用方程 (1) 计算雷诺数。为此, 考虑到在步骤3.1 中测量的杆 () 的直径, 用方程 (5) 确定的逼近速度 (), 以及步骤4.3.1 中确定的运动粘度
- 找到工作流体的运动粘度 (例如水 m
- 两相数的测定: 在自由流的时间线中, 杆尾的涡旋以不同的速度运动。因此, 涡脱落的频率需要独立估计。
- 定义固定参考杆的下游。此参考可以是连接到隧道外部的细字符串或添加到流过程视频中的数字线。
- 计算涡脱落循环的次数,, 在定义的时间段内越过参照.
在图 2(a) 中演示了旋涡脱落循环。 - 从以下等式计算脱落频率:
- 使用等式 (2) 中的方程 (5) 和 (6) 的结果来计算两相数。
2/秒)。
在图 2(a) 中演示了旋涡脱落循环。
流体运动由于其控制规律的非线性性质, 导致了复杂的流型。这些流动模式受许多因素的影响, 其中之一是流过一个障碍, 如一个钝体。一个钝体是一个物体, 由于其形状, 导致其表面的分离流动。根据流动条件, 这种流动可能会变得不稳定, 在尾流中产生振荡流动模式, 称为旋涡脱落。该视频将介绍由钝体造成的流动分离和旋涡脱落的基本知识, 并演示用于可视化产生的流模式的技术。
首先, 让我们来考虑流速 U 无穷大的水的均匀稳定流动, 称为自由流速接近圆柱体。边界层在物体表面的分离导致形成漩涡围绕身体, 最终分离到尾迹。当周期性的脱离发生时, 漩涡产生在身体后面的低压交替区域。这个过程被称为冯卡门涡街。这种重复模式发生在一定范围的雷诺数, 一个无量纲参数定义为惯性力与粘性力的比值。在这里, 怒江是流体的运动粘度, V 是特征速度或 U 无穷大在这种情况下, D 是圆筒直径。例如, 在以下演示中的设置中, 当雷诺数为五左右时, 该流在气缸后面有两个稳定的计数器旋转涡旋。随着雷诺数的增加, 这些涡旋沿着流动的方向拉长。当雷诺数达到大约37时, 由于压力和动量之间的不平衡, 尾迹变得不稳定并且振荡正弦。旋涡从气缸中脱落的频率不是恒定的, 而是随雷诺数的值而变化的。这种脱落频率的特点是两相数, 这是另一个无量纲参数。两相数定义为 f 是旋涡脱落频率。流态的实验分析使用四种类型的流线。路径线是给定流体粒子随水流移动而跟随的路径。条纹线是所有流体粒子的连续轨迹, 其运动来源于同一位置。流线是一条假想的线, 它瞬时地与速度场相切。请注意, 路径线、条纹线和流线在稳定的流动条件下相互重合。在当前流动, 这对应于流动的区域从钝体或从它的苏醒的影响足够远。另一方面, 在非恒定流动条件下, 路径线、条纹线和流线不同。在当前流中, 这基本上对应于钝体的尾迹。最后, 时间线是流体粒子的连续轨迹, 在同一时刻被释放到流中。在下面的实验中, 我们将使用一张连续的微小氢气泡来分析使用时间线和条纹线的流动模式。现在, 让我们来看看如何设置流实验。
首先, 根据所示的电气图装配设备。在试验段下游端的水中固定正极。接下来, 将负极固定在上游。这应该是在水流到达研究对象之前, 气泡被释放到流中的点附近。打开流程设备。然后将频率控制器的刻度盘设置为两个位置, 以建立平均每秒0.04 米的平均速度。此速度对应于每秒50到负第五立方米的流速。现在打开直流电源, 将电压增加到大约25伏, 电流约190毫安。在信号发生器上, 将输出设置为一个零伏的方波, 并在其高位置关闭电路, 并在低位置打开它的五伏方波信号。将直流偏移量最大化至五伏, 使电路始终闭合, 系统连续生成气泡。若要生成时间线, 请将信号发生器中的 DC 偏移量更改为一伏。然后将方波的频率设置为10赫兹。时间线将在流程中产生。然后将方波的对称性设置为负两个, 以增加时间线之间的空间。
首先用 SI 单位的卡尺测量杆的直径。固定负极的圆柱形杆的下游。将高光投射到氢泡层上, 确保光线不直接落在视线后面, 以防止成像系统的过度饱和。将可视化系统与标尺对齐, 以便在照相机前面仅显示圆形尖。在可视化窗口和杆的下游添加一个标记, 以使用它作为参考点来计算涡脱落循环。
首先测量在气泡片上由标尺投射的阴影的宽度。在杆上进行测量, 避免距离失真。使用标尺直径确定转换因素从机器单位到现实世界单位。接下来, 选择一组几乎不失真的时间线远离钝体和其唤醒的影响。测量机器单位中第一个和最后一个时间线之间的距离。计算组中的时间线数, 并记下方波的频率。从下面的等式中确定接近的流速。现在利用水的运动粘度, 计算雷诺数。接下来, 通过观察杆尾的涡旋来确定两相数。请注意, 与自由流中的时间线相比, 涡旋的运动速度是不同的。使用固定的字符串作为参考, 计算涡脱落循环的次数, NS, 在定义的时间段内越过参考点。计算脱落频率。然后使用结果计算两相数。
现在我们已经进行了程序和分析, 让我们来看看结果。使用雷诺数与两相数之间的关系可以确定结果的有效性。系数 St * 和 m 取决于雷诺数范围, 可以在文献中找到。这个例子中的雷诺数是115。因此, St * 和 m 的值可以用来计算两相数。两相数的计算值为 0.172, 这与实测值0.169 有很好的关联。当实验采用不同的操作参数进行时, 雷诺和两相数的计算与两个数之间的数学关系很好地相关。这显示了气泡法如何能很好地用来理解钝体周围的流动模式。
了解流模式对于许多类型的工程应用的设计和运行是必不可少的。桥梁和近海石油钻井平台的支柱是设计来抵御水流流过结构时所造成的湍流。了解某一给定结构的旋涡脱落频率对其设计至关重要。在这方面, 工程师必须确保结构的固有频率不是这样, 它会与旋涡脱落频率共振, 因为这将不可避免地导致结构的灾难性故障。研究流线型物体 (如空气箔或船体) 周围的流体流动也是必不可少的。通过利用流线, 工程师可以确定参数, 如飞机失速的角度, 甚至估计基于流速的升力特性。
你刚刚看了朱庇特的视频在一个钝体周围的可视化流线。你现在应该了解流体流动模式和冯卡门涡街的基础知识, 如何建立一个实验来可视化这些流动模式, 以及如何研究流动行为。谢谢收看
Subscription Required. Please recommend JoVE to your librarian.
Results
图 2显示了 Kármàn 涡街的氢气泡可视化的两个代表性结果。图 2(a) 显示了 streaklines 的一个例子, 如氢气泡片中的扰动所证明的那样。该图像用于在机器单元中提取杆的直径。图 2(B) 显示一个时间表领域的例子。该图像用于估计逼近的流体速度。从这个特定的实验提取的参数总结在表2。
Table2.代表性结果为流动通过一个圆筒.
| 参数 | 值 |
| D_o | 0.003 m |
| D_i | 14.528 分 |
| f_s | 2.169 赫兹 |
| f_tl | 10赫兹 |
| 我 | 130.167 "分" |
| m | 4842.67 "分" 捉 "m" |
| N_s | 60 |
| N_tl | 7 |
| t | 27.66 s |
| U_∞ | 0.0384 米/秒 |
| ν | 1.004× [10] ^ (-6) m2/秒 |
| 重新 | 115 |
| 圣 | 0.169 |
由于雷诺数为 115, 目前的例子, 这个结果的有效性可以用等式 (3) 来检验
(7)
从中我们得到:
(8)
将这一估计与我们的实验结果进行比较 (参见表2以供参考), 我们可以得出结论, 我们的实验提供了一个令人满意的结果。图 5显示了与公式 (7) 的预测相比较的一组实验结果。
图 5.实验结果。对比目前的实验结果与预测的雷诺数和两相数之间的关系的流动过一个圆形圆筒.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
在这项研究中, 利用氢气气泡, 以提取定性和定量信息从流动的图像周围的圆柱体。从这些实验中提取的定量信息包括自由流速度 ()、旋涡脱落频率 ()、雷诺数 (Re) 和两相数 (St).特别是, St vs Re 的结果与先前的研究有很好的一致性 [3]。
由于在当前实验中使用的速度慢, 气泡片中的扰动产生了五花肉气泡层。这些条纹基本上是 streaklines 的。随着氢气气泡片向下游移动, 这些 streaklines 变厚, 变得更加不规则。这是自由流中湍流强度的结果。由于气泡离开测试段前, 在呈现出明显的分散作用时, 隧道的速度会随之增加而减弱。Streaklines 也可以生产在预先选定的地点, 通过涂层的电线, 而留下的小部分, 它暴露在水中。
目前的流动行为是直接适用于过去的工程结构, 如桥梁和海上石油钻机, 风力涡轮机塔, 或电源线杆等的支柱。事实上, 这种行为是由钝体所展示的, 而不是圆柱状的, 如天空铲运机。考虑到旋涡产生的流体结构相互作用, 使结构振荡, 知道涡脱落频率的给定结构将暴露是关键的设计。在这方面, 工程师必须确保结构的固有频率不是这样, 它会与旋涡脱落频率产生共鸣, 因为这种影响将不可避免地导致结构的灾难性故障。使用适当的结垢定律 [10] 和水洞中的氢气气泡, 工程师可以在施工前模拟水流与结构的相互作用, 以确保其设计是安全的, 或者是发现它是否需要修改。
除了钝体, 氢气气泡可视化是一个非常强大的工具, 研究围绕流线型机构, 如翼型或船体。利用这一技术产生的流线, 可以确定失速发生的角度, 甚至估计基于流速的升力特性。更重要的是, 流体线的变形模式将有助于工程师优化其设计。
氢气泡的可视化并不局限于像上面提到的外部流。该方法还可用于观察明渠或全封闭流系统的流量。在后一种情况下, 墙壁需要是透明的, 以确保光学通道。例如, 如果一个人有兴趣设计一个流扩散器的亚声速流, 氢气气泡可以用来确定几何和流动条件, 扩散将表现出流分离和不稳定。根据这些观察, 设计可以进行实验优化, 以确保其正确的功能。
Subscription Required. Please recommend JoVE to your librarian.
References
- Zöllner, F. Leonardo da Vinci 1452-1519: sketches and drawings, Taschen, 2004.
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Adrian, Ronald J., and Jerry Westerweel. Particle Image Velocimetry. Cambridge University Press, 2011.
- Gerrard, J. H., The wakes of cylindrical bluff bodies at low Reynolds number, Phil. Trans. Roy. Soc. (London) Ser. A, Vol. 288, No. 1354, pp. 351-382 (1978)
- Coutanceau, M. and Bouard, R., Experimental determination of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow, J. Fluid Mech., Vol. 79, Part 2, pp. 231-256 (1977)
- Kovásznay, L. S. G., Hot-wire investigation of the wake behind cylinders at low Reynolds numbers, Proc. Roy. Soc. (London) Ser. A, Vol. 198, pp. 174-190 (1949)
- Fey, U., M. König, and H. Eckelmann. A new Strouhal-Reynolds-number relationship for the circular cylinder in the range
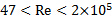. Physics of Fluids, 10(7):1547, 1998. - Maas, H.-G., A. Grün, and D. Papantoniou. Particle Tracking in three dimensional turbulent flows - Part I: Photogrammetric determination of particle coordinates. Experiments in Fluids Vol. 15, pp. 133-146, 1993.
- Malik, N., T. Dracos, and D. Papantoniou Particle Tracking in three dimensional turbulent flows - Part II: Particle tracking. Experiments in Fluids Vol. 15, pp. 279-294, 1993.
- Tropea, C., A.L. Yarin, and J.F. Foss. Springer Handbook of Experimental Fluid Mechanics. Vol. 1. Springer Science & Business Media, 2007.
- Monaghan, J. J., and J. B. Kajtar. Leonardo da Vinci's turbulent tank in two dimensions. European Journal of Mechanics-B/Fluids. 44:1-9, 2014.
- Becker, H.A. Dimensionless parameters: theory and methodology. Wiley, 1976.
