5.2: Gas Laws: Boyle's, Gay-Lussac, Charles', Avogadro's, and Ideal Gas Law
Through experiments, scientists established the mathematical relationships between pairs of variables, such as pressure and temperature, pressure and volume, volume and temperature, and volume and moles, that hold for an ideal gas.
Pressure and Temperature: Gay-Lussac’s Law (Amontons’s Law)
Imagine filling a rigid container attached to a pressure gauge with gas and then sealing the container so that no gas may escape. If the container is cooled, the gas inside likewise gets colder, and its pressure is observed to decrease. Since the container is rigid and tightly sealed, both the volume and number of moles of gas remain constant. If the sphere is heated, the gas inside gets hotter, and the pressure increases.
Temperature and pressure are linearly related, and this relationship is observed for any sample of gas confined to a constant volume. If the temperature is on the kelvin scale, then P and T are directly proportional (again, when volume and moles of gas are held constant); if the temperature on the kelvin scale increases by a certain factor, the gas pressure increases by the same factor.
This pressure-temperature relationship for gases is known as Gay-Lussac’s law. The law states that the pressure of a given amount of gas is directly proportional to its temperature on the kelvin scale when the volume is held constant. Mathematically, this can be written as:

where k is a proportionality constant that depends on the identity, amount, and volume of the gas. For a confined, constant volume of gas, the ratio P/T is therefore constant (i.e., P/T = k). If the gas is initially at ‘Condition 1’ (with P = P1 and T = T1), and changes to ‘Condition 2’ (with P = P2 and T = T2), then
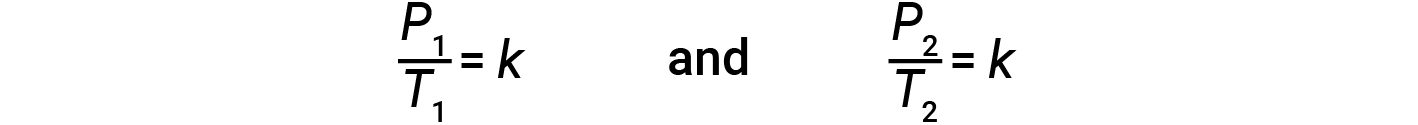
Therefore,
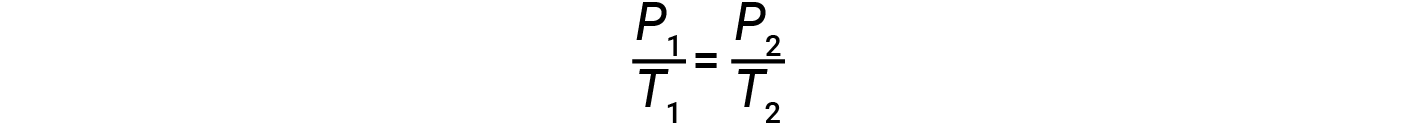
Note that for any gas law calculation, the temperatures must be on the kelvin scale.
Volume and Temperature: Charles’s Law
If a balloon is filled with air and sealed, then the balloon contains a specific amount of air at atmospheric pressure (1 atm). If the balloon is placed in a refrigerator, the gas inside gets cold, and the balloon shrinks (although both the amount of gas and its pressure remain constant). If the balloon is made very cold, it will shrink a great deal. When it is warmed up, the balloon will expand again.
This is an example of the effect of temperature on the volume of a given amount of a confined gas at constant pressure. The volume increases as the temperature increases, and the volume decreases as the temperature decreases.
The relationship between the volume and temperature of a given amount of gas at constant pressure is known as Charles’s law. The law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant.
Mathematically, this can be written as:
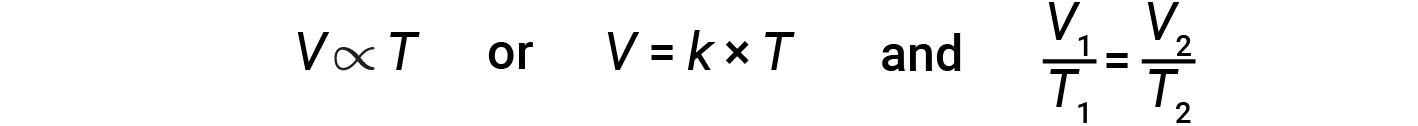
where k is a proportionality constant that depends on the amount and pressure of the gas. For a confined gas at constant pressure, the ratio V/T is constant.
Volume and Pressure: Boyle’s Law
If an airtight syringe is partially filled with air, then the syringe contains a specific amount of air at a constant temperature, say 25 °C. If the plunger is slowly pressed while the temperature remains constant, then the gas in the syringe is compressed into a smaller volume and its pressure increases. If the plunger is extracted, the volume of the gas increases and the pressure decreases.
Decreasing the volume of a contained gas will increase its pressure, and increasing its volume will decrease its pressure. If the volume increases by a certain factor, the pressure decreases by the same factor, and vice versa. Therefore, pressure and volume exhibit inverse proportionality: proportionality: Increasing the pressure results in a decrease in the volume of the gas. Mathematically this can be written:
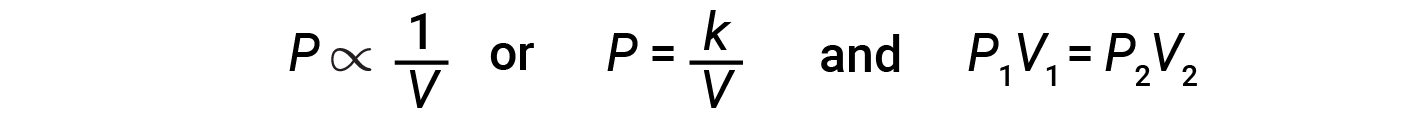
where k is a constant. A plot of P versus V displays a hyperbola. Graphs with curved lines are difficult to read accurately at low or high values of the variables, and they are more difficult to use in fitting theoretical equations and parameters to experimental data. For those reasons, scientists often try to find a way to “linearize” their data. Graphically, the relationship between pressure and volume is shown by plotting the inverse of the pressure versus the volume, or the inverse of volume versus the pressure.
The relationship between the volume and pressure of a given amount of gas at constant temperature is given by Boyle’s law: The volume of a given amount of gas held at constant temperature is inversely proportional to the pressure under which it is measured.
Moles of Gas and Volume: Avogadro’s Law
The Italian scientist Amedeo Avogadro advanced a hypothesis in 1811 to account for the behavior of gases, stating that equal volumes of all gases, measured under the same conditions of temperature and pressure, contain the same number of molecules. Over time, this relationship was supported by many experimental observations as expressed by Avogadro’s law: For a confined gas, the volume (V) and the number of moles (n) are directly proportional if the pressure and temperature both remain constant.
In equation form, this is written as:
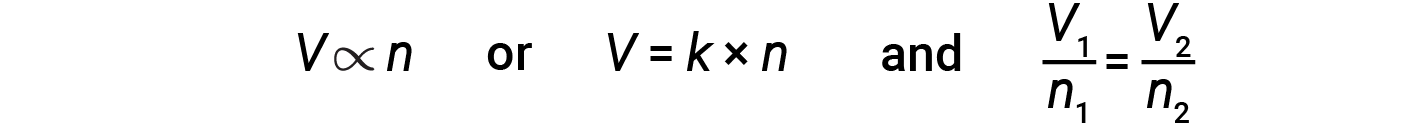
Mathematical relationships can also be determined for the other variable pairs, such as P versus n, and n versus T.
The Ideal Gas Law
Combining these four laws yields the ideal gas law, a relation between the pressure, volume, temperature, and number of moles of a gas:
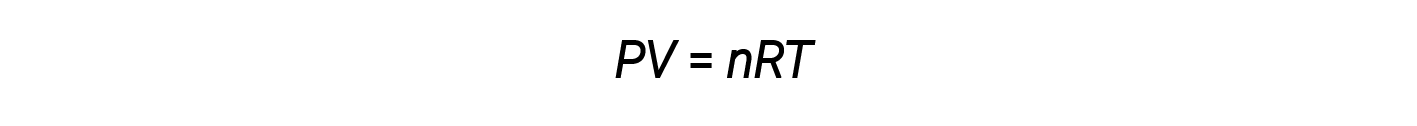
Here, R is a constant called the ideal gas constant or the universal gas constant. The units used to express pressure, volume, and temperature determine the proper form of the gas constant as required by dimensional analysis. The most commonly encountered values of R are 0.08206 L⋅atm mol–1⋅K–1 and 8.314 kPa⋅L mol–1⋅K–1.
Gases whose properties of P, V, and T are accurately described by the ideal gas law (or the other gas laws) are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that is only reasonable for gases under conditions of relatively low pressure and high temperature.
The ideal gas equation contains five terms, the gas constant R and the variable properties P, V, n, and T. Specifying any four of these terms will permit the use of the ideal gas law to calculate the fifth term.
If the number of moles of an ideal gas is kept constant under two different sets of conditions, a useful mathematical relationship called the combined gas law (using units of atm, L, and K) is obtained:
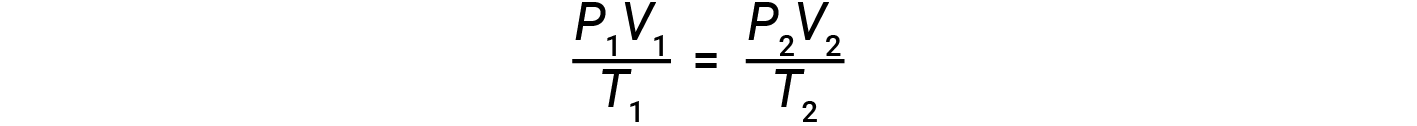
Both sets of conditions are equal to the product of n × R (where n = the number of moles of the gas and R is the ideal gas law constant).
This text is adapted from Openstax, Chemistry 2e, Section 9.2: Relating Pressure, Volume, Amount, and Temperature: The Ideal Gas Law.


