14.6: Calcul des concentrations d'équilibre
Il est essentiel de pouvoir calculer les concentrations à l'équilibre dans de nombreux domaines de la science et de la technologie, par exemple dans la formulation et le dosage des produits pharmaceutiques. Après l'ingestion ou l'injection d'un médicament, il est généralement impliqué dans plusieurs équilibres chimiques qui impactent sa concentration ultime dans le système corporel d'intérêt. La connaissance des aspects quantitatifs de ces équilibres est nécessaire pour calculer une dose qui sollicitera l'effet thérapeutique désiré.
Un type plus difficile de calcul d'équilibre peut être celui dans lequel les concentrations à l'équilibre sont déduites à partir des concentrations initiales et d'une constante d'équilibre. Pour ces calculs, une approche en quatre étapes est généralement utile :
- Identifier le sens dans lequel la réaction se poursuivra pour atteindre l'équilibre ;
- Concevoir un tableau ICE ;
- Calculer les changements de concentration et, par la suite, les concentrations d'équilibre ;
- Confirmer les concentrations à l'équilibre calculées.
Calcul des concentrations à l'équilibre
Dans certaines conditions, la constante d'équilibre Kc pour la décomposition de PCl5(g) en PCl3(g) et Cl2(g) est de 0,0211. La méthode ci-dessus peut être utilisée pour déterminer les concentrations à l'équilibre de PCl5, PCl3 et Cl2 dans un mélange qui contenait initialement seulement PCl5 à une concentration de 1,00 M.
Étape 1. Déterminer le sens de la réaction.
L'équation équilibrée pour la décomposition de PCl5 est
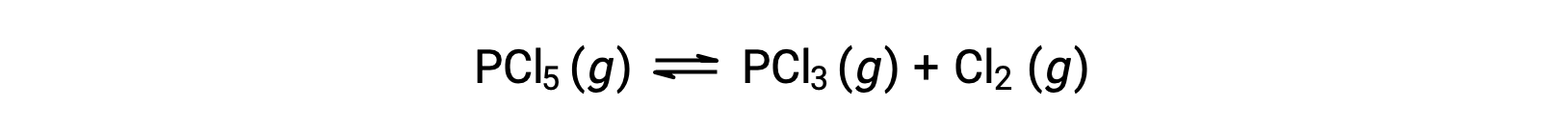
Étant donné que seul le réactif est initialement présent, Qc = 0, et la réaction se fera vers la droite.
Étape 2. Concevoir un tableau ICE.
| PCl5 (g) | PCl3 (g) | Cl2 (g) | |
| Concentration initiale (M) | 1,00 | 0 | 0 |
| Changement (M) | −x | +x | +x |
| Concentration à l'équilibre (M) | 1,00 − x | x | x |
Étape 3. Résoudre pour déterminer le changement et les concentrations à l'équilibre.
La substitution des concentrations à l'équilibre dans l'équation de la constante d'équilibre donne
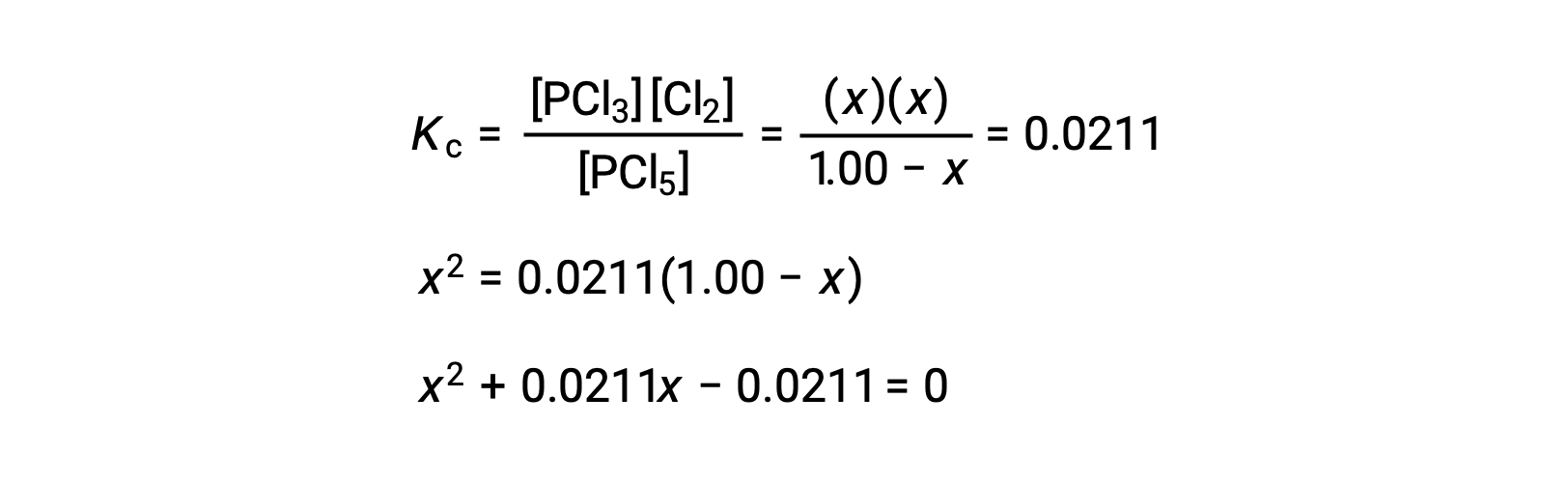
Une équation de la forme ax2 + bx + c = 0 peut être réorganisée pour résoudre x :
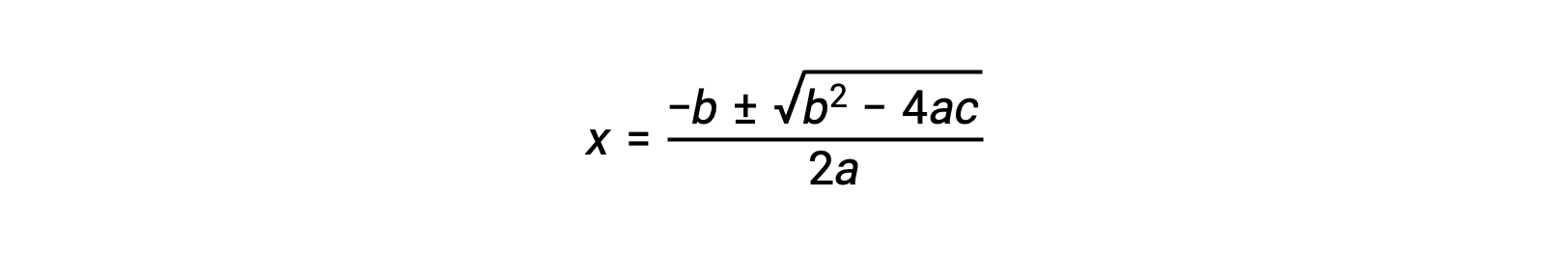
Dans ce cas, a = 1, b = 0,0211 et c = −0,0211. Le remplacement de a, b et c par les valeurs appropriées donne :
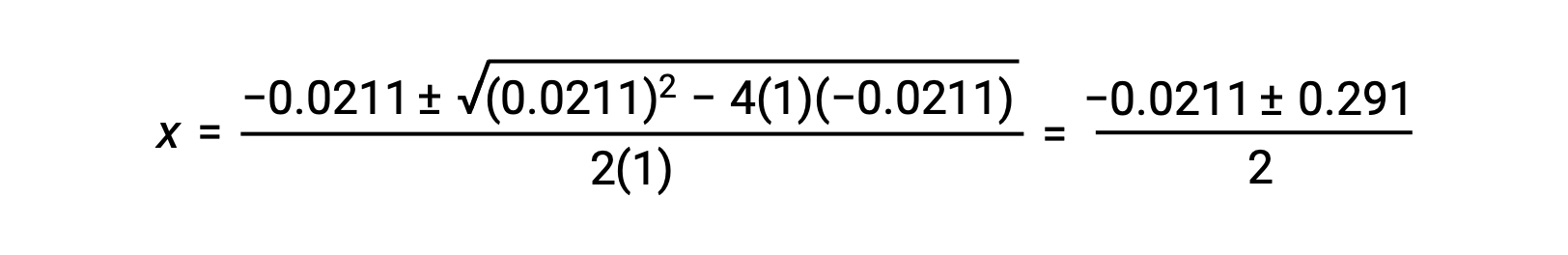
Les deux racines du quadratique sont donc,
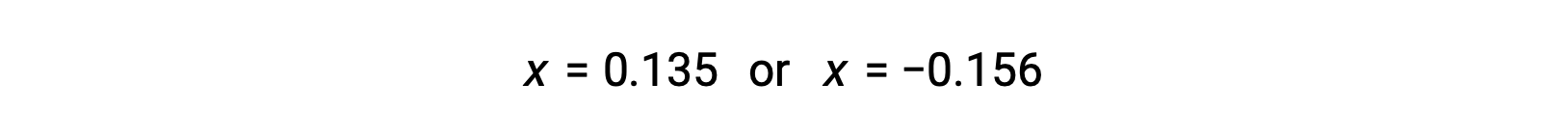
Pour ce scénario, seule la racine positive est physiquement significative (les concentrations sont soit zéro, soit positives), et donc x = 0,135 M. Les concentrations à l'équilibre sont
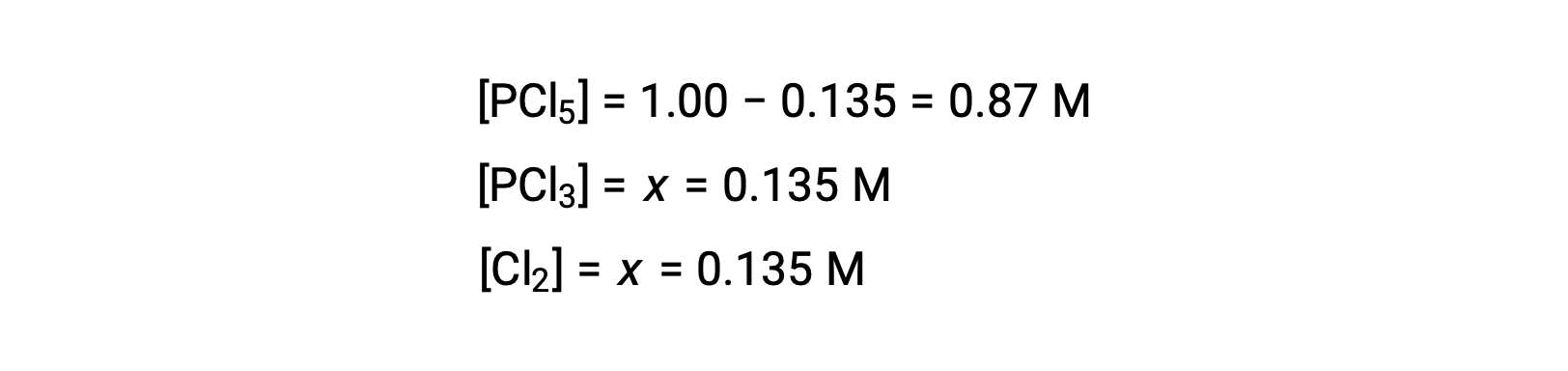
Étape 4. Confirmer les concentrations à l'équilibre calculées.
La substitution dans l'expression de Kc (pour vérifier le calcul) donne
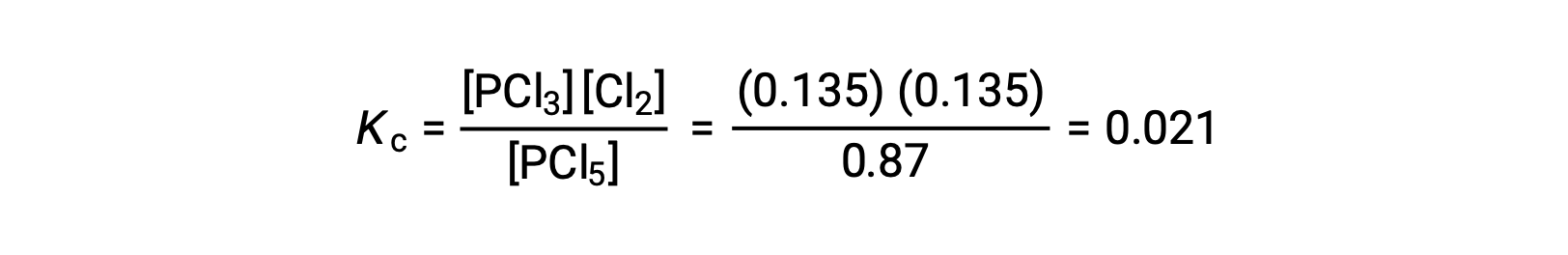
La constante d'équilibre calculée à partir des concentrations à l'équilibre est égale à la valeur de Kc donnée dans le problème (lorsqu'elle est arrondie au nombre approprié de chiffres significatifs).
Ce texte a été adapté d'Openstax, Chimie 2e, Section 13.4 Calculs d'équilibre.


