17.8: 標準自由エネルギの変化の計算
1気圧、298 Kという標準的な条件で起こる反応の自由エネルギー変化を、標準自由エネルギー変化といいます。自由エネルギーは状態関数であるため、その値は系の初期状態と終状態の条件にのみ依存します。物理・化学反応の自由エネルギー変化を計算するための便利で一般的な方法は、広く利用されている標準状態の熱力学データを利用することです。一つの方法は、標準的なエンタルピーとエントロピーを用いて、次の関係式に従って標準的な自由エネルギー変化 ΔG°を計算することです。
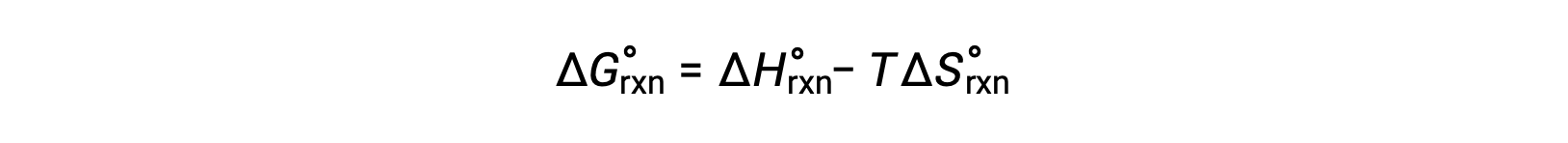
反応の標準自由エネルギー変化は、反応に関与する反応物および生成物の標準生成自由エネルギー ΔGf°の値から計算することもできます。標準生成自由エネルギーとは、標準状態の元素から1 molの物質を生成する際に生じる自由エネルギー変化のことです。標準生成エンタルピーと同様に、 ΔGf°は定義上、標準状態の単体ではゼロです。次の反応について、
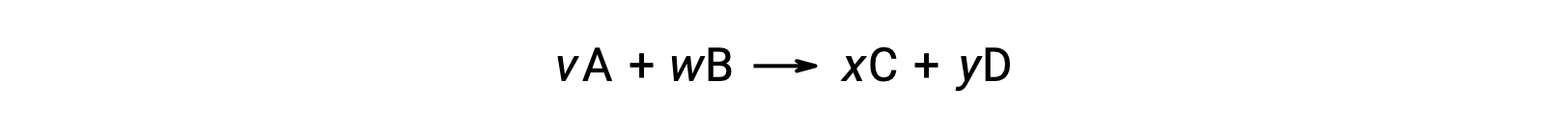
は、室温での標準的な自由エネルギー変化として計算することができます。
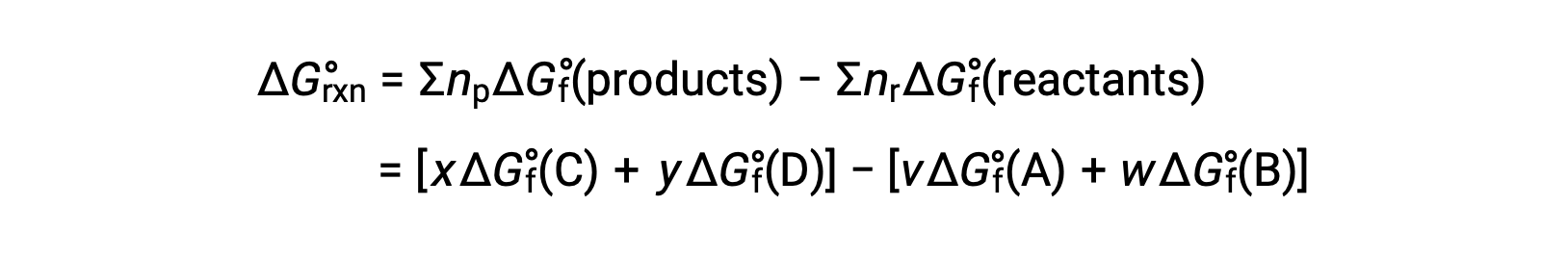
上記のような反応の自由エネルギー変化を計算するために生成自由エネルギーを使用できるのは、 ΔGが状態関数であるからです。このやり方はエンタルピー変化を計算する際にヘスの法則を利用することと類似しています。水の蒸発を例に考えよう。
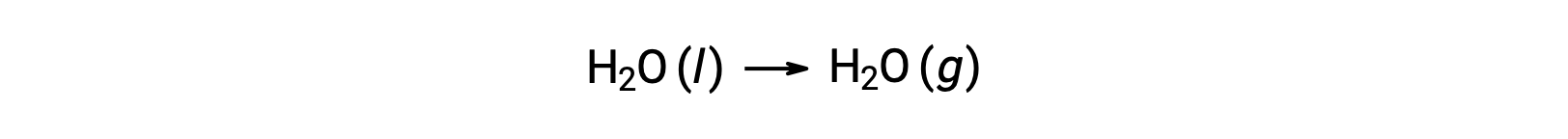
この過程を表す式は、水の2つの相の生成反応を加えることで導き出すことができる(液相の反応は逆にする)。反応の自由エネルギー変化は、加えられた2つの反応の自由エネルギー変化の合計です。
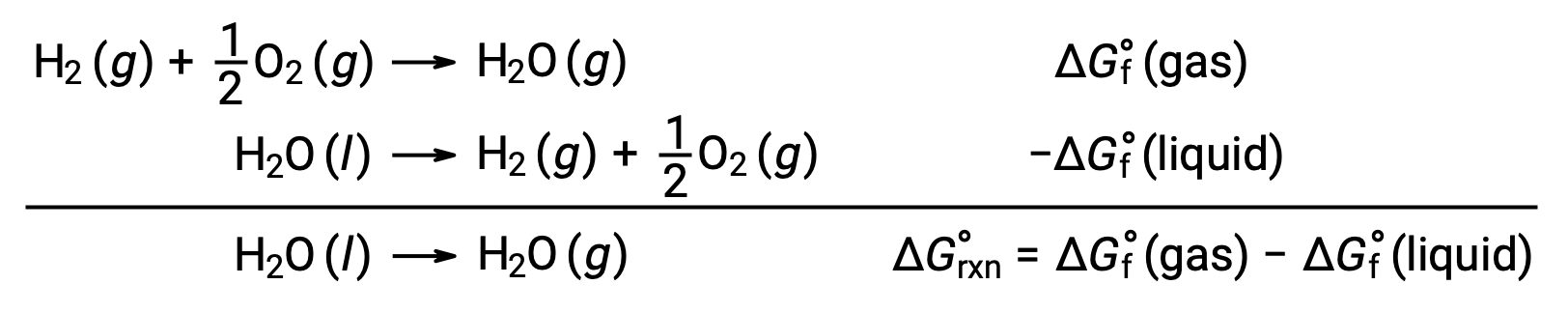
この方法は、非自発的な反応を自発的な反応と組み合わせることで強制的に進行させる場合にも用いることができます。例えば、硫化亜鉛から亜鉛の単体を生成させることは、 ΔG°1の正の値で示されるように、熱力学的に自発的ではありません。
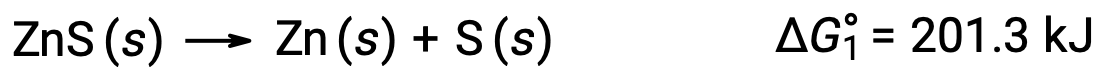
硫化鉱から亜鉛を製造する工業的なプロセスでは、この分解反応を熱力学的に有利な硫黄の酸化反応と組み合わせます。

足し合わされた反応は負の自由エネルギー変化を示すため、自発的に進行します。
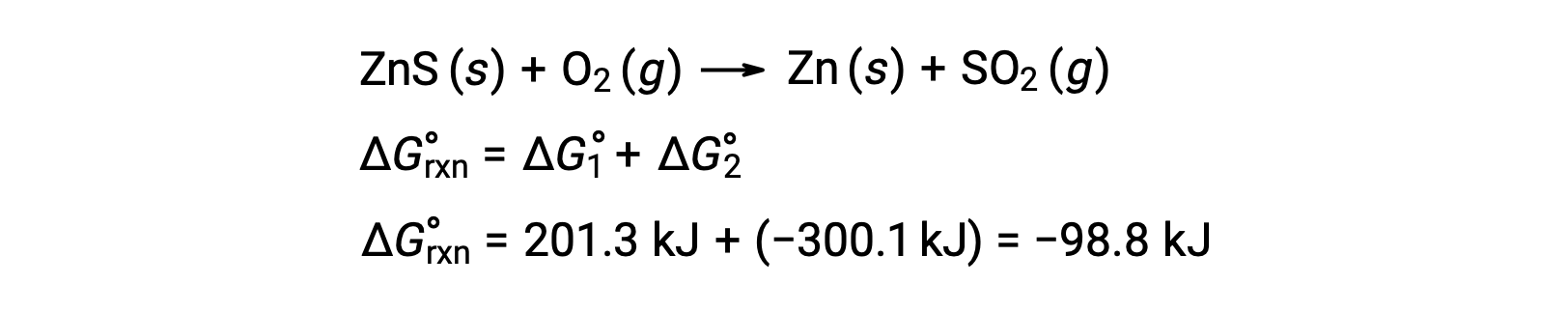
この製造プロセスは一般的に高温で行われるため、標準的な自由エネルギー値を用いて得られたこの結果はあくまで推定にしか用いることが出来ません。しかし、計算の要点は同様です。
上記の文章は以下から引用しました。Openstax, Chemistry 2e, Chapter 16.4: Free Energy.


