Overview
Fonte: Ricardo Mejia-Alvarez, Hussam Hikmat Jabbar e Mahmoud N. Abdullatif, Departamento de Engenharia Mecânica, Michigan State University, East Lansing, MI
Devido à natureza não linear de suas leis de governo, o movimento fluido induz padrões de fluxo complicados. Entender a natureza desses padrões tem sido objeto de intenso escrutínio há séculos. Embora computadores pessoais e supercomputadores sejam amplamente usados para deduzir padrões de fluxo de fluidos, suas capacidades ainda são insuficientes para determinar o comportamento exato de fluxo para geometrias complexas ou fluxos altamente inerciais (por exemplo, quando o momento domina sobre a resistência viscosa). Com isso em mente, uma infinidade de técnicas experimentais para tornar evidentes padrões de fluxo que podem atingir regimes de fluxo e geometrias inacessíveis às ferramentas teóricas e computacionais.
Esta demonstração investigará o fluxo de fluidos em torno de um corpo blefe. Um corpo blefe é um objeto que, devido à sua forma, causa fluxo separado sobre a maior parte de sua superfície. Isso contrasta com um corpo simplificado, como um aerofólio, que está alinhado no córrego e causa menos separação de fluxo. O objetivo deste estudo é usar bolhas de hidrogênio como método de visualização de padrões de fluxo. As bolhas de hidrogênio são produzidas através da eletrólise usando uma fonte de energia DC submergindo seus eletrodos na água. Bolhas de hidrogênio são formadas no eletrodo negativo, que precisa ser um fio muito fino para garantir que as bolhas permaneçam pequenas e rastreiem o movimento do fluido de forma mais eficaz. Este método é adequado para fluxos laminar constantes e instáveis, e é baseado nas linhas de fluxo básicas que descrevem a natureza do fluxo em torno dos objetos. [1-3]
Este artigo se concentra em descrever a implementação da técnica, incluindo detalhes sobre o equipamento e sua instalação. Em seguida, a técnica é usada para demonstrar o uso de duas das linhas básicas de fluxo para caracterizar o fluxo em torno de um cilindro circular. Estas linhas de fluxo são usadas para estimar alguns parâmetros importantes de fluxo, como a velocidade de fluxo e o número de Reynolds, e para determinar padrões de fluxo.
Principles
Nesta configuração, consideraremos um fluxo constante uniforme de água com velocidade 
(apelidada de velocidade de fluxo livre) aproximando-se de um cilindro circular (Figura 1). Dependendo das condições de fluxo caracterizadas pelo número de Reynolds, esse fluxo pode se tornar instável e dar origem ao derramamento de vórtice. O derramamento de vórtice é típico em corpos de blefe que, ao contrário de corpos simplificados, exibem separação de camadas de fronteira sobre uma parte substancial de sua superfície. Essa separação da camada de fronteira leva à formação de vórtices atrás do corpo que poderia eventualmente se desprender periodicamente na esteira. Quando ocorre o descolamento periódico, os vórtices geram áreas alternadas de baixa pressão atrás do corpo que podem se tornar cargas ressonantes se a frequência de derramamento coincidir com a frequência natural do corpo. Este processo de derramamento de vórtice é chamado de "Rua von Kármàn vortex" (Figura 2). Este padrão repetitivo de vórtices giratórios é causado pela separação de fluxo instável ao redor do corpo blefe e ocorre em certas faixas de número de Reynolds. Evitar esse cenário é de importância significativa na concepção de estruturas de engenharia, como pilhas de fumaça e pilares de pontes, uma vez que poderia resultar em uma falha catastrófica.
Figura 1. Passe por um cilindro circular. Esquema de configuração básica. Um fluxo homogêneo com velocidade 
se aproxima de um cilindro reto de diâmetro cujo eixo de 
simetria é perpendicular à velocidade que se aproxima.
O número de Reynolds é um parâmetro inafundado definido como a razão de forças inerciais com forças viscosas:
(1)
Onde 
está a viscosidade cinemática do fluido, 
uma velocidade característica (no caso atual) e 
o diâmetro do cilindro. O número de Reynolds é sem dúvida o parâmetro mais importante na caracterização do fluxo de fluidos e será usado durante todo o experimento atual como a métrica para o surgimento da rua von Kármàn vortex. Em particular, quando o número de Reynolds é em torno de 5, o fluxo exibe dois vórtices contra-rotativos estáveis atrás do cilindro. À medida que o número de Reynolds aumenta, esses dois vórtices se alongam na direção do fluxo. Quando o número de Reynolds atinge um valor de aproximadamente 37, o rastro se torna instável e começa a oscilar sinuosamente como resultado de um desequilíbrio entre pressão e impulso. Um aumento adicional no número de Reynolds até 47 faz com que os dois vórtices contra-rotativos se desprendem do cilindro em uma sequência alternada que segue a oscilação da vigília sinusoidal [4,5,6].
A frequência com que os vórtices são derramados fora do cilindro não é constante; varia com o valor do número de Reynolds. A frequência de derramamento é caracterizada pelo número Strouhal, que é o outro parâmetro de relevância a dimensionável nesta configuração de fluxo de fluidos particulares:
(2)
Aqui, 
está a frequência de derramamento de vórtice e as escalas de comprimento e velocidade são as mesmas do número de Reynolds. A frequência de derramamento de vórtice pode então ser caracterizada pelo número strouhal como uma função linear da raiz quadrada inversa do número de Reynolds [7]:
(3)
Esta função nem sempre é monótona, exibe outras transições como resultado de instabilidades secundárias devidos à não linearidade do fluxo de fluidos. Como resultado, os coeficientes 
e 
mudariam de acordo com a faixa numérica de Reynolds. A Tabela 1 mostra os valores desses coeficientes para os regimes de escoamento que têm sido bem caracterizados na literatura [7].
Durante os atuais experimentos, usaremos linhas de fluxo para estudar o fluxo externo em torno de um cilindro circular. Estas linhas de fluxo são definidas da seguinte forma:
• Linha de caminho: caminho que uma partícula fluida segue à medida que se move com o fluxo.
• Streakline: lócus contínuo de todas as partículas fluidas cujo movimento se originou no mesmo local espacial.
• Linha do tempo: conjunto de partículas fluidas que foram marcadas no mesmo instante de tempo enquanto formavam um lócus contínuo.
• Simplificar: linha contínua que está em todos os lugares tangente ao campo de velocidade em um instante no tempo.
As três primeiras linhas são relativamente fáceis de gerar experimentalmente, enquanto as simplificações são apenas um conceito matemático que, em geral, tem que ser produzido após o processamento de uma captura instantânea do campo de velocidade. Embora isso seja sempre verdade, a análise simplifica significativamente em fluxos constantes porque pathlines, streaklines e aerodinâmicas coincidem entre si. Por outro lado, essas linhas geralmente não coincidem entre si em fluxos instáveis. A implementação desta técnica é geralmente simples e requer apenas equipamentos de baixo custo, em oposição a técnicas mais sofisticadas e caras, como Velocimetria de Imagem de Partículas [1], Velocimetria de Rastreamento de Partículas [8,9], e Velocimetria de Etiqueta molecular [10].
Figura 2. Resultados representativos. (A) folha contínua de bolhas de hidrogênio que mostra linhas de traço como resultado de perturbações a montante. A sombra lançada pela haste é usada para determinar a conversão da máquina para unidades reais. Um ciclo de derramamento de vórtice também é ilustrado para ajudar a determinar a frequência de derramamento adequadamente. (B) cronogramas gerados com bolhas de hidrogênio. Uma vez que a frequência da linha do tempo é bem definida, elas podem ser usadas para medir a velocidade de fluxo com precisão; a contagem dos cronogramas incluídos nas linhas vermelhas será usada para esta estimativa. Clique aqui para ver uma versão maior desta figura.
Tabela 1. Valores dos coeficientes 
e 
para diferentes intervalos numéricos de Reynolds (a partir de [8]).
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. Produzir uma folha contínua de bolhas:
- Defina o equipamento de acordo com o diagrama elétrico mostrado na Figura 3.
- Fixar o eletrodo positivo na água na extremidade a jusante da seção de teste (ver Figura 4 para referência).
- Fixar o eletrodo negativo rio acima e perto do ponto de interesse para liberar as bolhas no fluxo antes que o fluxo atinja o objeto de estudo (ver Figura 4 para referência). A água completa o circuito entre os dois eletrodos.
- Ligue a instalação de fluxo
- Ajuste o mostrador do controlador de frequência para a posição 2. Isso estabelecerá uma taxa de fluxo de cerca de 9x10-4 m3/s.
- Ligue a fonte de alimentação DC e aumente a tensão para cerca de 25 V, a corrente se definirá em torno de 190 mA.
- Defina a forma de onda no gerador de sinal para onda quadrada (símbolo:
). Isso gera um sinal quadrado de 0 V - 5 V que ativa o relé de estado sólido (fechando o circuito) em sua posição alta e abre-o na posição baixa - Para este caso em particular, a frequência da onda quadrada não é importante. Só precisa ser não-zero.
- Maximize o deslocamento DC (+5 V) no gerador de sinal. Com essa configuração, o circuito é sempre fechado e o sistema gera bolhas continuamente.
). Isso gera um sinal quadrado de 0 V - 5 V que ativa o relé de estado sólido (fechando o circuito) em sua posição alta e abre-o na posição baixa
Figura 3. Diagrama de conexões.
Figura 4. Seção de teste. O fluxo vai da esquerda para a direita. O eletrodo negativo gera uma camada de bolhas de hidrogênio que são varridas com o fluxo. O eletrodo positivo é definido na extremidade a jusante da seção de teste para evitar seus distúrbios. Clique aqui para ver uma versão maior desta figura.
2. Para produzir cronogramas:
- Ligue a instalação de fluxo
- Ajuste o mostrador do controlador de frequência para a posição 2. Isso estabelecerá uma taxa de fluxo de cerca de 9x10-4 m3/s.
- Ligue a fonte de alimentação DC e aumente a tensão para cerca de 25 V, a corrente se definirá em torno de 190 mA.
- Defina a forma de onda no gerador de sinal para onda quadrada (símbolo: ). Isso gera um sinal quadrado de 0 V - 5 V que ativa o relé de estado sólido (fechando o circuito) em sua posição alta e o desativa (abrindo o circuito) na posição baixa
- Coloque o deslocamento dc no gerador de sinal em +1 V.
- Defina a frequência da onda quadrada no gerador de sinal a 10 Hz.
- Defina a simetria da onda quadrada ligeiramente negativa (-2) para aumentar o espaço entre as linhas do tempo enquanto conserva a frequência certa.
3. Usar linhas de fluxo para estudar as ruas de vórtice von Kármàn:
- Meça o diâmetro da haste,
usando uma pinça. Use unidades S.I. para esta medição (m). - Fixar uma haste cilíndrica a jusante do eletrodo negativo.
- Lance a luz da lâmpada de descarga de alta intensidade na camada de bolhas de hidrogênio. Certifique-se de que a luz não está diretamente atrás da linha de visão para evitar a supersaturação do sistema de imagem
- Alinhar o sistema de visualização com a haste; de uma forma que apenas a ponta circular é visível na frente da câmera.
- Adicione uma marca na janela de visualização e a jusante da haste para usá-la como referência para contar ciclos de galpão de vórtice por tempo de unidade.
usando uma pinça. Use unidades S.I. para esta medição (m).4. Análise de dados para fluxo após um cilindro circular:
- Determinação do fator de conversão de unidades de máquinas para unidades espaciais reais:
- Meça a largura da sombra lançada pela haste na folha de bolhas (ver figura 2(A) para referência). Leve esta medida para a direita na haste para evitar distorções com a distância. Este é o diâmetro da haste em unidades de máquina,
(pontos ou pixels, dependendo do formato) - Use a seguinte equação para determinar o fator de conversão de unidades de máquinas para unidades do mundo real:
- Meça a largura da sombra lançada pela haste na folha de bolhas (ver figura 2(A) para referência). Leve esta medida para a direita na haste para evitar distorções com a distância. Este é o diâmetro da haste em unidades de máquina,
- Determinação da velocidade de fluxo:
- Escolha um grupo de cronogramas não distincionados rio acima do corpo blefe.
- Meça a distância entre a primeira e a última linha do tempo em unidades de máquinas
(pontos ou pixels). - Conte o número de cronogramas no grupo,
. - Tome nota da frequência do sinal de onda quadrada produzido pelo gerador de sinal,
. - Determine a velocidade de fluxo que se aproxima da seguinte equação:
- Determinação do número de Reynolds:
- Encontre a viscosidade cinemática do fluido de trabalho (por exemplo, água
m2/s). - Calcule o número de Reynolds usando equação (1). Para isso, considerando o diâmetro da haste
medida na etapa 3.1, a velocidade de aproximação 
( ) determinada com equação (5), e a viscosidade cinemática determinada na etapa 4.3.1
- Encontre a viscosidade cinemática do fluido de trabalho (por exemplo, água
- Determinação do número strouhal: os vórtices na esteira da haste estão se movendo em uma velocidade diferente como as linhas do tempo no fluxo livre. Portanto, a frequência de derramamento de vórtice precisa ser estimada independentemente.
- Defina uma referência fixa a jusante da haste. Esta referência pode ser uma corda fina anexada ao exterior do túnel ou uma linha digital adicionada a um vídeo do processo de fluxo.
- Conte o número de ciclos de derramamento de vórtice,
cruzando a referência durante um período de tempo definido 
. Um ciclo de derramamento de vórtice é ilustrado na Figura 2(A). - Calcule a frequência de derramamento a partir da seguinte equação:
- Use os resultados das equações (5) e (6) na equação (2) para calcular o número strouhal.
(pontos ou pixels, dependendo do formato)
(pontos ou pixels).
.
.
m2/s).
medida na etapa 3.1, a velocidade de aproximação 
cruzando a referência durante um período de tempo definido 
. Um ciclo de derramamento de vórtice é ilustrado na Figura 2(A).
Devido à natureza não linear de suas leis de governo, o movimento fluido induz padrões de fluxo complicados. Esses padrões de fluxo são influenciados por muitos fatores, um dos quais é passar por um obstáculo, como um corpo blefe. Um corpo blefe é um objeto que, devido à sua forma, causa fluxo separado sobre a maior parte de sua superfície. Dependendo das condições de fluxo, esse fluxo pode se tornar instável, dando origem a padrões de fluxo oscilantes na esteira chamada derramamento de vórtice. Este vídeo introduzirá o básico da separação de fluxo e derramamento de vórtice causado por um corpo blefe e demonstrará uma técnica usada para visualizar os padrões de fluxo resultantes.
Primeiro, vamos considerar o fluxo uniforme e constante de água com a velocidade U infinito chamado a velocidade livre de fluxo se aproximando de um cilindro circular. A separação da camada de fronteira na superfície do objeto leva à formação de vórtices ao redor do corpo que eventualmente se desprendem na esteira. Quando ocorre o desprendimento periódico, os vórtices geram áreas alternadas de baixa pressão atrás do corpo. Este processo é chamado de rua von karman vórtice. Este padrão repetitivo ocorre em certas faixas de número de Reynolds, um parâmetro a dimensionável definido como a razão de forças inerciais com forças viscosas. Aqui, nu é a viscosidade cinemática do fluido, V é a velocidade característica ou U infinito neste caso, e D é o diâmetro do cilindro. Por exemplo, na configuração na demonstração seguinte, quando o número de Reynolds é em torno de cinco, o fluxo exibe dois vórtices contra-rotativos estáveis atrás do cilindro. À medida que o número de Reynolds aumenta, esses vórtices se alongam na direção do fluxo. Quando o número de Reynolds atinge aproximadamente 37, o rastro se torna instável e oscila sinuosamente como resultado de um desequilíbrio entre pressão e impulso. A frequência em que os vórtices são derramados fora do cilindro não é constante, pelo contrário, varia com o valor do número reynolds. Esta frequência de derramamento é caracterizada pelo número Strouhal, que é outro parâmetro a dimensionado. O número strouhal é definido como mostrado onde f é a frequência de derramamento de vórtice. A análise experimental dos padrões de fluxo utiliza quatro tipos de linhas de fluxo. Uma linha de caminho é o caminho que uma determinada partícula fluida segue à medida que se move com o fluxo. Uma linha de raia é o lócus contínuo de todas as partículas fluidas cujo movimento se originou do mesmo local. Uma simplificação é uma linha imaginária que é instantaneamente e localmente tangente ao campo de velocidade. Observe que linhas de caminho, linhas de raia e aerodinâmicas coincidem entre si em condições constantes de fluxo. No fluxo atual, isso corresponde a regiões do fluxo rio acima do corpo blefe ou longe o suficiente da influência de sua esteira. Por outro lado, linhas de caminho, linhas de raia e aerodinâmicas diferem umas das outras sob condições de fluxo instável. No fluxo atual, isso corresponde basicamente ao rastro do corpo blefe. Finalmente, as linhas temporais são o lócus contínuo de partículas fluidas que foram liberadas ao fluxo no mesmo instante no tempo. No experimento seguinte, usaremos uma folha contínua de pequenas bolhas de hidrogênio para analisar padrões de fluxo usando linhas temporais e linhas de listras. Agora, vamos dar uma olhada em como configurar o experimento de fluxo.
Primeiro, monte o equipamento de acordo com o diagrama elétrico mostrado. Fixar o eletrodo positivo na água na extremidade a jusante da seção de teste. Em seguida, conserte o eletrodo negativo rio acima. Isso deve ser perto do ponto onde as bolhas são liberadas no córrego antes que o fluxo chegue ao objeto de estudo. Ligue a instalação de fluxo. Em seguida, defina o mostrador do controlador de frequência para posicionar dois, a fim de estabelecer uma velocidade média de cerca de 0,04 metros por segundo. Esta velocidade corresponde a uma taxa de fluxo de cerca de 50 a menos quinto metros cúbicos por segundo. Agora ligue a fonte de alimentação DC e aumente a tensão para cerca de 25 volts com a corrente em torno de 190 miliamperes. Em um gerador de sinal, ajuste a saída para uma onda quadrada com um sinal quadrado de zero volts a cinco volts que fecha o circuito em sua posição alta e abre-a na posição baixa. Maximize o deslocamento dc para cinco volts para que o circuito esteja sempre fechado e o sistema gere bolhas continuamente. Para produzir cronogramas, altere o deslocamento dc no gerador de sinal para um volt. Em seguida, definir a frequência da onda quadrada para 10 Hertz. Cronogramas serão produzidos no fluxo. Em seguida, defina a simetria da onda quadrada para menos dois, a fim de aumentar o espaço entre as linhas do tempo.
Primeiro meça o diâmetro da haste usando uma pinça em unidades SI. Fixar a haste cilíndrica rio abaixo do eletrodo negativo. Lance luz de alta intensidade na camada de bolhas de hidrogênio, certificando-se de que a luz não está diretamente atrás da linha de visão para evitar a saturação do sistema de imagem. Alinhe o sistema de visualização com a haste para que apenas a ponta circular seja visível na frente da câmera. Adicione uma marca na janela de visualização e rio abaixo da haste para usá-la como ponto de referência para contar ciclos de galpão de vórtice.
Primeiro meça a largura da sombra lançada pela haste na folha de bolhas. Leve a medida para a direita na haste para evitar distorções com a distância. Use o diâmetro da haste para determinar o fator de conversão de unidades de máquinas para unidades do mundo real. Em seguida, escolha um grupo de cronogramas quase não distincionados longe do corpo blefe e a influência de seu rastro. Meça a distância L entre o primeiro e o último cronograma em unidades de máquina. Conte o número de cronogramas no grupo e observe a frequência da onda quadrada. Determine a velocidade de fluxo que se aproxima da equação seguinte. Agora, usando a viscosidade cinemática da água, calcule o número de Reynolds. Em seguida, determine o número strouhal observando os vórtices na esteira da haste. Observe que os vórtices se movem em uma velocidade diferente em comparação com as linhas do tempo no fluxo livre. Usando a sequência fixa como referência, conte o número de ciclos de derramamento de vórtice, NS, cruzando o ponto de referência durante um período de tempo definido. Calcule a frequência de derramamento. Em seguida, use os resultados para calcular o número strouhal.
Agora que passamos por cima do procedimento e análise, vamos dar uma olhada nos resultados. A validade do resultado pode ser determinada usando uma relação entre o número de Reynolds e o número strouhal. Os coeficientes St* e m dependem da faixa numérica de Reynolds e podem ser encontrados na literatura. O número de Reynolds neste exemplo é 115. Assim, os valores de St* e m podem ser usados para calcular o número strouhal. O valor calculado para o número strouhal é de 0,172, o que se correlaciona bem com o valor medido de 0,169. Quando este experimento foi conduzido com diferentes parâmetros operacionais, os cálculos dos números reynolds e strouhal correlacionam-se bem com a relação matemática entre os dois números. Isso mostra o quão bem o método bolha pode ser usado para entender padrões de fluxo em torno de um corpo blefe.
Entender os padrões de fluxo é essencial para o projeto e o funcionamento de muitos tipos de aplicações de engenharia. Pilares de pontes e plataformas de petróleo offshore são projetados para suportar a turbulência causada pelo fluxo atual após a estrutura. Conhecer o vórtice que derrama frequências em que uma determinada estrutura será exposta é fundamental para o seu design. Nesse sentido, os engenheiros têm que ter certeza de que a frequência natural da estrutura não é tal que ressoará com a frequência de derramamento do vórtice, porque isso inevitavelmente levará a uma falha catastrófica da estrutura. Também é essencial estudar o fluxo de fluidos em torno de um objeto simplificado, como uma folha de ar ou casco de navio. Ao fazer uso de linhas de fluxo, os engenheiros podem determinar parâmetros como o ângulo em que um avião para ou mesmo estimar características de elevação com base na velocidade de fluxo.
Você acabou de ver o vídeo de Jove visualizando linhas de fluxo em torno de um corpo blefe. Agora você deve entender o básico dos padrões de fluxo de fluidos e a rua vórtice Von Karman, como configurar um experimento para visualizar esses padrões de fluxo, e como estudar o comportamento do fluxo. Obrigado por assistir.
Subscription Required. Please recommend JoVE to your librarian.
Results
A Figura 2 mostra dois resultados representativos de visualização de bolhas de hidrogênio de uma rua de vórtice von Kármàn. A Figura 2(A) mostra um exemplo de um campo de linhas de listras como evidenciado por distúrbios na folha de bolhas de hidrogênio. Esta imagem é usada para extrair o diâmetro da haste em unidades de máquinas. A Figura 2(B) mostra um exemplo de um campo de cronogramas. Esta imagem é usada para estimar a velocidade do fluido que se aproxima. Os parâmetros extraídos deste experimento em particular são resumidos na tabela 2.
Tabela 2. Resultados representativos para o fluxo passado um cilindro circular.
| Parâmetro | Valor |
| D_o | 0,003 m |
| D_i | 14.528 pts |
| f_s | 2.169 Hz |
| f_tl | 10 Hz |
| L | 130.167 "pts" |
| M | 4842,67 "pts" |
| N_s | 60 |
| N_tl | 7 |
| T | 27.66 s |
| U_∞ | 0,0384 m/s |
| ν | 1.004×[10]^(-6) m2/s |
| Re | 115 |
| St | 0.169 |
Uma vez que o número de Reynolds é 115 para o exemplo atual, a validade deste resultado pode ser testada usando equação (3) para 
(7)
A partir do qual obtemos:
(8)
Depois de comparar essa estimativa com nosso resultado experimental (ver tabela 2 para referência), podemos concluir que nosso experimento ofereceu um resultado satisfatório. A Figura 5 mostra um conjunto de resultados experimentais em comparação com as previsões da equação (7).
Figura 5. Resultados experimentais. Comparação dos resultados experimentais atuais com previsões da relação entre o número de Reynolds e o número strouhal para fluxo após um cilindro circular.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
Neste estudo, demonstrou-se o uso de bolhas de hidrogênio para extrair informações qualitativas e quantitativas a partir de imagens de fluxo em torno de um cilindro circular. As informações quantitativas extraídas desses experimentos incluíam a velocidade de fluxo livre ( ), frequência de derramamento de vórtice (), número de Reynolds (Re) e o número strouhal (St). Em particular, os resultados de St vs Re apresentaram concordância muito boa com estudos anteriores [3].
Devido à velocidade lenta usada nos experimentos atuais, perturbações na folha de bolhas produzem uma camada de bolha streaky. Essas listras são basicamente streaklines. À medida que a folha de bolhas de hidrogênio viaja rio abaixo, essas linhas se engrossem e se tornem mais irregulares. Este é o resultado da intensidade da turbulência no fluxo livre. O efeito é atenuado à medida que a velocidade do túnel é aumentada, uma vez que as bolhas deixam a seção de teste antes de apresentar uma dispersão significativa. As linhas de listras também podem ser produzidas em locais pré-selecionados, revestindo o fio, deixando pequenas partes dele expostas à água.
O comportamento de fluxo atual é diretamente aplicável ao fluxo de estruturas de engenharia passadas, como os pilares de pontes e plataformas de petróleo offshore, torres de turbinas eólicas ou postes de linha de energia para citar alguns. E, de fato, esse comportamento é exibido por corpos blefe com geometrias diferentes de cilíndricas, como raspadores de céu. Dado que os vórtices geram interações fluido-estrutura que fazem as estruturas oscilarem, saber as frequências de derramamento de vórtice nas quais uma determinada estrutura será exposta é fundamental para seu design. Nesse sentido, o engenheiro tem que ter certeza de que a frequência natural da estrutura não é tal que ressoará com a frequência de derramamento do vórtice, pois esse efeito inevitavelmente levará a uma falha catastrófica da estrutura. Usando leis de dimensionamento apropriadas [10] e bolhas de hidrogênio em um túnel de água, um engenheiro pode simular a interação do fluxo com uma estrutura antes de sua construção para se certificar de que seu projeto é seguro ou para descobrir se ele precisa de alguma modificação.
Além dos corpos blefe, a visualização da bolha de hidrogênio é uma ferramenta muito poderosa para estudar o fluxo em torno de corpos simplificados, como aerofólios ou cascos de navios. Ao fazer uso de linhas de fluxo geradas com esta técnica, pode-se determinar parâmetros como o ângulo de ataque em que a parada ocorre, ou mesmo estimar características de elevação com base na velocidade de fluxo. Mais importante, o padrão de distorção das linhas de fluidos ajudará o engenheiro a otimizar seu design.
A visualização com bolhas de hidrogênio não se restringe a fluxos externos como o mencionado acima. Este método também pode ser usado para observar o fluxo através de canais abertos ou sistemas de fluxo totalmente confinados. Neste último caso, as paredes precisarão ser transparentes para garantir o acesso óptico. Por exemplo, se alguém estiver interessado em projetar um difusor de fluxo para fluxo subsónico, bolhas de hidrogênio podem ser usadas para determinar condições geométricas e de fluxo para as quais o difusor exibirá separação de fluxo e instabilidade. Com base nessas observações, o design poderia ser otimizado experimentalmente para garantir sua funcionalidade adequada.
Subscription Required. Please recommend JoVE to your librarian.
References
- Zöllner, F. Leonardo da Vinci 1452-1519: sketches and drawings, Taschen, 2004.
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Adrian, Ronald J., and Jerry Westerweel. Particle Image Velocimetry. Cambridge University Press, 2011.
- Gerrard, J. H., The wakes of cylindrical bluff bodies at low Reynolds number, Phil. Trans. Roy. Soc. (London) Ser. A, Vol. 288, No. 1354, pp. 351-382 (1978)
- Coutanceau, M. and Bouard, R., Experimental determination of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow, J. Fluid Mech., Vol. 79, Part 2, pp. 231-256 (1977)
- Kovásznay, L. S. G., Hot-wire investigation of the wake behind cylinders at low Reynolds numbers, Proc. Roy. Soc. (London) Ser. A, Vol. 198, pp. 174-190 (1949)
- Fey, U., M. König, and H. Eckelmann. A new Strouhal-Reynolds-number relationship for the circular cylinder in the range
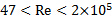. Physics of Fluids, 10(7):1547, 1998. - Maas, H.-G., A. Grün, and D. Papantoniou. Particle Tracking in three dimensional turbulent flows - Part I: Photogrammetric determination of particle coordinates. Experiments in Fluids Vol. 15, pp. 133-146, 1993.
- Malik, N., T. Dracos, and D. Papantoniou Particle Tracking in three dimensional turbulent flows - Part II: Particle tracking. Experiments in Fluids Vol. 15, pp. 279-294, 1993.
- Tropea, C., A.L. Yarin, and J.F. Foss. Springer Handbook of Experimental Fluid Mechanics. Vol. 1. Springer Science & Business Media, 2007.
- Monaghan, J. J., and J. B. Kajtar. Leonardo da Vinci's turbulent tank in two dimensions. European Journal of Mechanics-B/Fluids. 44:1-9, 2014.
- Becker, H.A. Dimensionless parameters: theory and methodology. Wiley, 1976.
