Overview
출처: 타마라 M. 파워스, 텍사스 A&M 대학교 화학학과
금속 카보닐 복합체는 유기금속 복합체뿐만 아니라 촉매의 합성을 위한 금속 전구체로 사용된다. 적외선(IR) 분광법은 CO함유 화합물의 가장 활용되고 유익한 특성화 방법 중 하나입니다. 분자의 대칭을 설명하기 위해 수학을 사용하는 그룹 이론또는 수학을 사용하는 것은 분자 내의 IR 활성 C-O 진동 모드의 수를 예측하는 방법을 제공한다. IR에서 C-O 뻗어의 수를 실험적으로 관찰하는 것은 금속 카보닐 복합체의 기하학 및 구조를 확립하는 직접적인 방법입니다.
이 비디오에서는, 시스 및 트랜스형태(도1)에존재할 수 있는 몰리브덴 카보닐 복합모(CO)4[P(OPh)3]2를합성합니다. 우리는 그룹 이론과 IR 분광기를 사용하여 어떤 isomer가 격리되는지 결정할 것입니다.
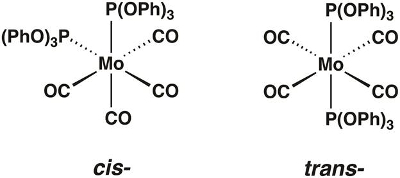
그림 1. 시스- 및 모(CO)의 트랜스 -isomers4[P (OPh)3]2.
Principles
선택 규칙:
선택 규칙은 지정된 분자에 대해 가능한 한 양자 상태에서 다른 양자 상태로 전자 전이 수를 결정합니다. IR 분광법은 분자의 지면 상태에서 진동 전이를 프로브, v = 0, 첫 번째 흥분 상태, v = 1. 선형 및 비선형 분자에 대한 진동 자유도(일반 진동 모드)의 수는 각각 방정식 1과 방정식 2를사용하여 계산할 수 있습니다.
3N - 5(1)
3N - 6(2)
여기서 N = 분자의 원자 수
IR이 활성화되기 위해 정상적인 진동 모드가 활성화되려면 분자의 이폴이 변경되어야 합니다. 따라서 이폴의 변화가 발생하지 않는 정상적인 진동 모드는 IR비활성상태입니다. 활성 IR 모드의 수는 그룹 이론을 사용하여 결정할 수 있습니다.
그룹 이론:
화학자는 분자의 대칭과 물리적 특성 사이의 관계를 이해하기 위해 그룹 이론을사용합니다. 그룹 이론의 범위가 너무 광범위하여 이 비디오에서 엄격하게 커버할 수 없지만, 간단한 조정 단지에 그룹 이론을 적용하고 IR 활성 진동 모드의 수를 예측하는 데 어떻게 사용할 수 있는지 보여주는 데 필요한 도구를 제공할 것입니다. 이를 입증하기 위해, 우리는 분자 시스모(CO)4[P(OPh)3]2에그룹 이론의 적용을 통해 걸을 것이다.
첫째, 분자의 포인트 그룹을 결정해야 합니다. 점 그룹은 주어진 분자에 존재하는 대칭 원소를 설명하기 위해 사용됩니다. 시스-모(CO) 4[P(OPh)3]2의점군을 결정하기 위해, 분자에 존재하는 대칭 원소에 대한 일련의 질문을 하는 대칭 트리라고 불리는 플로우 차트를 사용할 수 있다(도2). 표 1은 대칭 트리에 포함된 모든 대칭 요소를 요약합니다. 대칭 트리를 사용하고, 리간드 P(OPh)3이 포인트 리간드(그 리간드의 대칭을 무시하면서) 포인트 리간드라고 가정하면, 우리는 시스모(CO)4[P(OPh)3]2가 포인트 그룹 C2v에 있음을 발견한다.

그림 2. 점 그룹 결정에 사용되는 대칭 트리입니다.
표 1. 포인트 그룹 결정에 사용되는 대칭 요소입니다.
| 대칭 요소 | 사용된 기호 | 예* |
| 신원 | E |  |
| 회전축 (회전 360°/n) |
Cn |  |
| 수평 미러 평면 (xy 평면에 대한 반사) |
σh |  |
| 수직 거울 평면 (xz 또는 yz 평면에 대한 반사) |
σv |  |
| 대각선 거울 비행기 (xz와 yz 평면 사이의 반사) |
σd |  |
| 반전 센터 | 나는 |  |
| 부적절한 회전 축 (회전360°/n, 회전 축에 수직반사) |
Sn |  |
| *예는 리간드 1–6이 동등한 옥타헤드랄 단지의 예입니다. 작업을 수행하면 결과 분자가 원래 구성과 구별할 수 없어야 합니다. | ||
다음 단계를 위해 지정된 점 그룹에 있는 모든 대칭을 설명하는 문자 테이블을 소개해야 합니다. 포인트 그룹 C2v의 문자 표는 아래에 표시됩니다.
| C2v | E | C2 | σv(xz) | σv'(yz) | ||
| A1 | 1 | 1 | 1 | 1 | z | x2,y2,z2 |
| A2 | 1 | 1 | −1 | −1 | Rz | xy |
| B1 | 1 | −1 | 1 | −1 | x, Ry | xz |
| B2 | 1 | −1 | −1 | 1 | y, Rx | yz |
포인트 그룹은 문자 테이블의 왼쪽 상단 모서리에 표시됩니다. 포인트 그룹의 오른쪽에 해당 지점 그룹에 내재된 모든 대칭 작업이 나열됩니다. 후속 행에는 해당 점 그룹에 포함된 모든 대칭 표현(불가역 표현, 즉 A1)과원자 궤도의 대칭성뿐만 아니라 x-y-및 z축을 따라 선형 이동에 대해 알려줄 수 있는 함수대칭이 나열됩니다.
포인트 그룹 C2v용문자테이블을 사용하여, 분자시스-모(CO)4[P(OPh)3]2 (도 3)에서C-O 스트레치 모드의 재유도 표현(Γ빨간색)을생성한다. 재구성 가능한 표현 또는 돌이킬 수 없는 표현의 선형 조합은 문자 테이블 내의 각각의 대칭 작업을 분자 내의 진동에 적용하고 변경되지 않은 C-O 진동 횟수를 기록하여 생성될 수 있다(공간에서 동일한 위치에서). 예를 들어, 시스-모(CO)4[P(OPh)3]2에서C-O 진동에 ID 대칭 요소를 적용하면 4개의 진동 화살표가 모두 동일한 위치에 남아 있다. 따라서, 우리의 재현 표현의 첫 번째 값은 4입니다. 이 연습을 계속하면 아래와 같이 재현 가능한 표현을 생성합니다.
| C2v | E | C2 | σv(xz) | σv'(yz) |
| Γ레드 | 4 | 0 | 2 | 2 |
다음으로, C 2v 문자 테이블을 사용하여 시스모(CO)4[P(OPh)3]2내에서 C-O 진동에 대해 Γ빨간색을 생성하는 돌이킬 수 없는 표현의 선형 조합을 찾습니다. 재추론 표현의 감소는 수학식 3에도시된 환원 수식을 사용하여 달성될 수 있다.
 (3)
(3)
어디:
ni = 회수 가능한 표현에서 발생하는 돌이킬 수없는 표현 횟수
h = 그룹의 순서(총 대칭 작업 수)
c = 작업 클래스
gc = 클래스의 작업 수
클래스의작업에 대한 돌이킬 수없는 표현의 문자= θ i = 문자
클래스의 작업에 대한 재현 가능한 표현의 θr = 문자
문자 테이블 C2v의돌이킬 수없는 표현 각각에 대한 방정식 3을 사용하여 빨간색 = 2 A1+ B 1 + B 2가Γ 것을 발견합니다. 기여할 수 없는 세 표현, A1, B1및 B2는x-y-또는 z축으로 변환하기 때문에 IR활성입니다(문자 표에서 함수의 대칭 참조). 따라서 시스모(CO)4[P(OPh)3]2가 IR 스펙트럼에 4개의 C-O 스트레칭 모드를 전시할 것으로 예상됩니다.
요약하자면 분자의 IR 활성 진동 모드 수를 결정하기 위해 다음 단계가 필요합니다.
1. 분자의 점 그룹을 결정합니다.
2. 분자 내의 C-O 스트레칭 진동의 재현 가능한 표현을 생성합니다.
3. 방정식 3을사용하여 재현 가능한 표현을 줄입니다.
4. 3단계에서 감소된 표현에 존재하는 번역돌이킬 수 없는 표현의 수를 식별합니다.
우리는 트랜스 모(CO)4[P (OPh)3]2와함께 이러한 4 단계를 수행하면 분자가 1 활성 C-O 진동 모드를 가지고 있음을 발견한다.

그림 3. C-Mo(CO)4[P(OPh)3] 2에서CO 진동이 뻗어 있다.
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. 슐렌크 라인의 설정 (자세한 절차에 대 한, 검토 하시기 바랍니다 "솔벤트의 슐렌크 라인 전송" 유기 화학 시리즈의 필수 에서 비디오). 이 실험을 수행하기 전에 Schlenk 라인 안전을 검토해야 합니다. 유리 웨어는 사용하기 전에 별 균열에 대한 검사해야합니다. 액체N2를 사용하는 경우 O2가 슐렌크 라인 트랩에 응축되지 않도록주의해야 한다. 액체 N2 온도에서 O2는 응축되며 유기 용매가 있는 경우 폭발성입니다. O2가 응축되었거나 차가운 트랩에서 파란색 액체가 관찰된 것으로 의심되는 경우, 트랩을 동적 진공 상태에서 차갑게 둡니다. 액체 N2 트랩을 제거하거나 진공 펌프를 끄지 마십시오. 시간이 지남에 따라 액체 O2 펌프에 숭고할 것입니다; 모든 O2가 승화되면 액체 N 2 트랩을 제거하는 것이 안전합니다.
- 압력 방출 밸브를 닫습니다.
- N2 가스와 진공 펌프를 켭니다.
- 슐렌크 라인 진공이 최소 압력에 도달하면 액체 N2 또는 드라이 아이스/아세톤으로 콜드 트랩을 준비합니다.
- 차가운 함정을 조립합니다.
2. 모 (CO)4[P (OPh)3]2 (그림 4)1의 합성
참고: Mo(CO)4[P(OPh)3]2(슐렌크 라인 기술을 이용한 "Ti(III) 메탈로센의 합성" 비디오의 합성을 위해 표준 슐렌크 라인 기법을 사용한다. 금속 카보닐 복합체는 매우 독성이 있는 무료 CO의 공급원입니다. 일산화탄소 중독은 CO가 헤모글로빈에 결합할 때 발생하므로 신체에 산소 공급이 현저하게 감소합니다. 따라서 금속 카보닐 복합체를 취급하고 작업할 때 적절한 안전 조치를 취하는 것이 매우 중요합니다. 무료 CO를 생성하는 반응은 독성 가스에 대한 노출을 방지하기 위해 통풍이 잘 되는 후드에서 수행되어야 합니다.
- 1.6g(4.92mmol) Mo(CO)4(nbd= 2,5-노르보나디엔) 및 1.6mL(9.84mmol) 삼페닐 인스파이트(P(OPh)3)를100m 슐렌크 플라스크에 넣고 슐렌크 플라스크를 100m에 넣고 슐렌크 플라스크를 준비할 수 있다.
참고: Mo(CO)4(nbd) (((비시클로[2.2.1]hepta-2,5-diene))테트라카보릴몰리브덴(0)은 시그마 알드리히로부터 구입하거나 문헌 방법을 사용하여 합성할 수 있다. 2 - 캐뉼라 전송을 통해 슐렌크 플라스크에 20mL의 탈가스 디클로로메탄을 넣습니다.
- N2아래 실온에서 4 시간 동안 반응 혼합물을 저어.
- 진공 상태에서 휘발성을 제거하고 차가운 육산으로 생성된 침전액을 씻어넣습니다(각각 10mL, -78°C로 두 개의 세척).
- 15 분 동안 진공 상태에서 고체 제품을 건조.
- 육산용액에서 제품의 IR 스펙트럼을 측정합니다.

그림 4. 모(CO)4[P(OPh)3]2의합성.
그룹 이론은 분자 대칭을 IR 활성 진동 모드와 같은 특성에 연결하는 수학적 모델입니다.
모든 분자는 고정된 점에 대하여 분자에 존재하는 모든 대칭 요소를 설명하는 점 단으로분류될 수 있습니다.
그룹 이론은 분자의 대칭이 진동 모드 및 기타 중요한 특성에 미치는 영향을 예측하기 위해 문자 테이블이라고하는 특수 테이블을 제공합니다.
이 비디오는 그룹 이론의 기본 원리에 대해 논의하고, Mo(CO)4[P(OPh)3]2의이소머의 합성 및 특성화 절차를 설명하고, 화학에서 그룹 이론의 몇 가지 응용 프로그램을 소개합니다.
분자 대칭은 분자의 구별할 수 없는 구성을 설명합니다. 둘 사이의 변환을 대칭 작업이라고하며, 이는 하나 이상의 대칭 요소와 관련하여 발생합니다.
다섯 가지 대칭 요소는 적절하고 부적절한 회전 축, 미러 평면, 반전 중심 및 ID입니다. 모든 분자에는 변화가 발생하지 않는 정체성 원소 또는 E가있습니다.
σ 레이블이 붙은 미러 평면은동일한 시작 및 끝 구성이 있는 반사 평면입니다. 분자는 하나 이상의 거울 평면을 가질 수 있습니다. 반전의 중심, i라고표시, 모든 원자가 반영되는 지점입니다.
적절한 회전 축은 분자가 동일한 구성으로 회전하는 축입니다. n은 회전 각도로 나눈 Cn으로표시됩니다.
Sn이라고표시된 부적절한 회전 축은 분자가 회전한 다음 수직 거울 평면을 통해 반사되는 축입니다. 분자는 두 개 이상의 회전 축을 가질 수 있습니다. 가장 높은 n을 가진 축은 주축입니다.
분자는 분자를 분류하는 데 필요한 대칭 작업을 식별하는 대칭 트리를사용하여 포인트 그룹에 할당됩니다.
예를 들어 BF3은 비선형입니다. 2보다 큰 축이 2개 이상인 축이 하나 이상 없습니다. 적어도 하나의 회전 축이 있습니다. 주요 축은 C3입니다. 주 축에 수직인 C2 축 3개, 주축에 수직인 미러 평면이 있습니다. 따라서, 붕소 트리플루오라이드는 D3h 포인트 그룹에 속한다.
각 점 그룹에는 필수 대칭 작업을 나열하는 문자 테이블이 있습니다. 각 행에는 해당 원자 궤도 및 선형 움직임과 함께 작업의 돌이킬 수 없는 표현이 포함되어 있습니다.
이러한 대칭 작업이 분자 특성에 미치는 영향을 평가하여 재현 가능한 표현이 생성됩니다. 이 표현을 줄이면 기여할 수 없는 표현이 됩니다.
이제 그룹 이론의 원리를 이해하게 되었으므로 Mo(CO)4[P(OPh)3] 2의이소머를합성하고 IR 스펙트럼을 그룹 이론별로 예측된 IR 활성 모드의 수와 비교하는 절차를 살펴보겠습니다.
절차를 시작하려면 슐렌크 라인 통풍구를 닫고 N2 가스의 흐름을 시작합니다. 진공 펌프를 켜고 시스템을 최소한의 압력으로 켜면 아세톤의 드라이 아이스로 진공 트랩을 식힙니다.
연기 후드에, Mo (CO)4(nbd)의 0.5 g을 측정하고 200 mL 슐렌크 플라스크에 몰리브덴 전구체를 배치합니다. 반응 플라스크에 스티어 바를 장착하고 플라스크에 유리 스토퍼를 스토퍼로 포장하십시오. 플라스크를 사이드 암을 통해 슐렌크 라인에연결하고, 5분 동안 선박을 대피시켜 캐뉼라 이송을 위해 플라스크를 준비하고, 그 다음에 는 플라스크를 N2로리필한다. 이 피난 및 리필 프로세스를 총 3회 반복합니다.
다음으로, CH 2Cl2의20mL가 들어있는 고무 중격이 장착 된 또 다른 슐렌크 플라스크를 준비하십시오. 플라스크를 슐렌크 라인에 연결하고 후드의 플라스크를고정합니다. 주사기를 사용하여, 트리페닐 인스파이트 0.87 mL을 그리고 슐렌크 플라스크에 분배한다. 슐렌크 라인 스톱콕이 N2에열려 있는지 확인하십시오. 10분 동안 용매를 통해N2를 버블링하여 CH2Cl 2/triphenyl 인산염 혼합물을 탈가스한다. 그런 다음 캐뉼라 전송을 사용하여 솔리드를 포함하는 플라스크에 솔루션을 추가합니다. N2 가스에 반응 플라스크를 열고 4 시간 동안 실온에서 혼합물을 저어.
반응이 끝나면 고무 중격을 유리 스토퍼로 교체하고 진공 상태에서 휘발성 용매를 제거하십시오.
그 결과 제품에 헥산을 넣고 침전물이 형성될 때까지 드라이 아이스/아세톤 욕조에서 간소하게 식힙니다. 침전물을 걸러내고 10mL의 차가운 육산으로 침전물을 두 번 세척하고 여과에 의해 고체를 수집합니다. 15 분 동안 진공 상태에서 고체 제품을 건조.
마지막으로, 육산에 제품의 일부를 용해하고 용액을 IR 셀에 로드합니다. 복합체의 IR 스펙트럼을 획득합니다.
이제 isomers에 포인트 그룹을 할당하고 예측된 IR 활성 모드를 IR 스펙트럼에 비교하여 제품이 시스 또는 트랜스 이소머인지 여부를 결정해 보겠습니다.
시스나 트랜스 이소머는 선형이 아니며 2개 이상의 주문이 있는 두 개 이상의 회전 축도 없습니다. 둘 다 둘 다 하나 이상의 회전 축을 가지고 있습니다. 시스 및 트랜스 이소마의 주축은 각각 C2 및 C4입니다.
시스 이소머는 C2 축에 수직인 C2 축 2개가 없으며 수직 거울 평면도 없습니다. C2 축을 포함하는 두 개의 미러 평면이 있으므로 포인트 그룹은 C2v입니다. 트랜스 이소머는 C2 축 4개에 수직으로 C 2 축 4개와 미러 평면을 가지고 있으므로 포인트 그룹은 D4h입니다.
다음으로, CO 스트레치의 재현 가능한 표현은 분자에 각 대칭 동작을 적용하고 공간에서 위치를 변경하지 않는 C-O 스트레치를 계산하여 생성됩니다.
C2v 테이블에는 C2축이 포함된 두 개의 미러 평면을 통해 ID, C2 회전 및 반사의 네 가지 작업이 있습니다. ID 작업에서 4개의 이폴 순간이 모두 제자리에 남아 있습니다. 4개의이폴 순간은 모두 C2 로테이션 후 다른 포지션을 취합니다. 두 개의 다폴 레멘트는 각 반사에 대해 동일한 위치에 남아 있습니다.
감소 공식은 재현 가능한 표현에서 각 돌이킬 수 없는 표현의 계수를 계산합니다. 포인트 그룹 순서는 대칭 작업 수입니다. 클래스는 대칭 작업의 유형입니다. 여기서 각 클래스의 작업 수는 1이며, 이는 전통적으로 문자 테이블에서 생략됩니다.
문자는 지정된 클래스의 표현에 해당하는 값입니다. 감소 공식이 적용되면 세 가지 돌이킬 수 없는 표현이 발견되고 하나는 두 번 발생합니다. 이러한 표현은 4개의 IR 활성 C-O 스트레스그와 일치하는 x, y또는 z 축으로 변환됩니다.
동일한 기술을 사용하여, 트랜스 이소머는 하나의 IR 활성 C-O 스트레치가 있는 것으로 나타났다. 몰리브덴 제품의 IR 스펙트럼은 2046, 1958 및 1942cm-1에서 최고조에달합니다. 해상도가 높은 데이터를 사용하면 네 번째 C-O 스트레치가 관찰될 수 있습니다. 얻어진 IR에 기초하여, 하나는 격리된 Mo(CO)4[P(OPh)3]2 복합체가 시스 이소머라고 결론을 내릴 수 있다.
그룹 이론은 유기 및 무기 화학에 널리 사용됩니다. 몇 가지 예를 살펴보겠습니다.
라만 분광법은 전자 구름의 편광성 변화를 수반하는 분자 진동을 감지합니다. CO2의 대칭 스트레치는 다폴 모멘트를 변경하지 않으므로 IR 활성이 아닙니다. 그러나 핵에서 멀리 이동하는 전자는 극성을 변화시켜 스트레치 라만 활성화를 이시합니다. 그룹 이론은 IR 활성 모드를 식별하는 데 사용되는 동일한 일반적인 방법을 따라 라만 활성 진동 모드를 식별할 수 있습니다.
분자 궤도 이론, 또는 MO 이론은 분자에서 결합을 설명하는 데 사용되는 모델입니다. 두 원자의 원자 궤도를 추가하고 빼면 간단한 해부학의 분자 궤도 다이어그램이 형성됩니다.
전이 금속 복합체의 MO 다이어그램을 생성하기 위해 과학자들은 그룹 이론을 사용하여 원자 궤도의 대칭 적응선형 조합을 생성하여 외부 원자 또는 리간드를 나타냅니다. 이는 리간드 원자 궤도의 재현 가능한 표현을 생성한 다음 이를 돌이킬 수 없는 표현으로 줄임으로써 달성됩니다.
금속 중심의 대칭 표현과 대칭 적응선형 조합은 다이어그램에서 비교됩니다. 이 모델에서는 동일한 대칭을 가진 궤도가 겹쳐서 두 개의 분자 궤도를 형성합니다.
그룹 이론에 대한 JoVE의 소개를 방금 시청했습니다. 분자 대칭의 기본 원리, 분자의 요점 그룹을 찾고, 그룹 이론이 유기 및 무기 화학에서 어떻게 사용되는지에 대한 몇 가지 예에 대해 잘 알고 있어야 합니다. 시청해 주셔서 감사합니다!
Subscription Required. Please recommend JoVE to your librarian.
Results

그림 5. 모 (CO)4[P (OPh)3]2의IR.
포화 탄화수소 (cm-1)의용액 IR : 2046 (s), 1958 (s), 1942 (대).
네 번째 공진은 고해상도 조건에서만 볼 수 있습니다. 따라서, 이 경우와 같이 4개의 공진 중 3개만 관찰될 수 있다.
획득된 IR에 기초하여, 우리는 Mo(CO)4[P(OPh)3]2가 분리되었다는 결론을 내릴 수 있다.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
이 비디오에서는 분자에서 IR 활성 진동 모드의 수를 예측하기 위해 그룹 이론을 사용하는 방법을 배웠습니다. 분자 모(CO)4[P(OPh)3]2를 합성하고 IR을 사용하여 어떤 이좀러가 분리되었는지 를 판단하였다. 우리는 제품이 시스-isomer와 일치하는 IR 스펙트럼에 세 개의 C-O 진동이 있음을 관찰했다.
그룹 이론은 화학자가 IR 활성 진동 모드를 예측할 뿐만 아니라 라만 분광법에서 관찰되는 진동, 회전 및 기타 저주파 모드를 예측하는 데 사용되는 강력한 도구입니다. 또한, 그룹 이론은 전이 금속 복합체 내의 결합을 설명하는 가장 널리 사용되는 모델인 분자 궤도(MO) 이론에서 구현된다. 유기 및 무기 화학자에 의해 사용되는 MO 다이어그램은 분자의 관찰된 반응성을 예측하고 설명할 수 있습니다.
1st,2nd및 3rd 행 금속 카보닐 복합체는 더 복잡한 유기 금속 화합물에 대한 금속 전구체로서 무기 합성에 널리 사용된다. 금속 카보닐 복합체를 가진 반응의 가장 일반적인 모형의 몇몇은 CO 리간드 치환, 금속 센터에 있는 redox 및 CO 단위에 뉴클레오필 공격을 포함합니다. 금속 카보닐 복합체 자체는 촉매에 널리 사용됩니다. 예를 들어, 수압포름, 알케인으로부터알데히드의 산업생산은 금속 카보닐 복합체 HCo(CO)3(도 6)에의해 촉매화된다.

그림 6. 금속 카보닐 복합체 HCo(CO)3에의한 하이드로포름화.
Subscription Required. Please recommend JoVE to your librarian.
References
- Fukumoto, K., Nakazawa, H. Geometrical isomerization of fac/mer-Mo(CO)3(phosphite)3 and cis/trans-Mo(CO)4(phosphite)2 catalyzed by Me3SiOSO2CF3. J Organomet Chem. 693(11), 1968-1974 (2008).
- Darensbourg, M. Y., Magdalena, P., Houliston, S. A., Kidwell, K. P., Spencer, D., Chojnacki, S. S., Reibenspies, J. H. Stereochemical nonrigidity in heterobimetallic complexes containing the bent metallocene-thiolate fragment. Inorg Chem. 31(8), 1487-1493 (1992).
- Darensbourg, M. Y., Darensbourg, D. J. Infrared Determination of Stereochemistry in Metal Complexes. J Chem Ed. 47(1), 33-35 (1970).




