Overview
Fuente: Tamara M. Powers, Departamento de química, Texas A & M University
Complejos de metal carbonilo se utilizan como metal precursores para la síntesis de complejos organometálicos como catalizadores. Espectroscopia infrarroja (IR) es uno de los métodos de caracterización más utilizada e informativo de CO que contienen compuestos. Teoría de grupos, o el uso de las matemáticas para describir la simetría de una molécula, proporciona un método para predecir el número de modos vibracionales activos de C O IR dentro de una molécula. Observar experimentalmente que el número de C-O se extiende en el IR es un método directo para establecer la geometría y estructura del carbonilo de metal complejo.
En este video, sintetizamos el molibdeno carbonilo complejo Mo(CO)4[P(OPh)3]2, que pueden existir en las formas cis y trans(figura 1). Usaremos teoría del grupo y la espectroscopia IR para determinar qué isómero aislado.
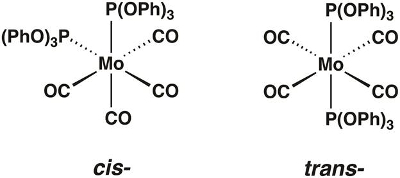
Figura 1. El cis- y trans-isómeros de Mo(CO)4[P(OPh)3]2.
Principles
Reglas de selección:
Reglas de selección determinan el número de transiciones electrónicas de un estado cuántico a otro, que es posible para una molécula dada. Espectroscopia IR sondas transiciones vibracionales de la molécula tierra, v = 0, al primer estado excitado, v = 1. El número de grados de libertad vibracional (modos normales de vibración) para moléculas lineales y no lineales puede calcularse usando la ecuación 1 y ecuación 2, respectivamente.
3N - 5 (1)
3N - 6 (2)
donde N = el número de átomos en la molécula de
De un modo normal de vibración que IR activo, dipolo de la molécula debe cambiar. Por lo tanto, cualquier modos normales de vibración donde no se produce un cambio en el dipolo son IR inactivo. El número de modos de IR activados puede ser determinado mediante teoría de grupos.
Teoría del grupo:
Químicos utilizan teoría de grupos para entender la relación entre la simetría y propiedades físicas de una molécula de. Mientras que el alcance de la teoría del grupo es demasiado amplio para cubrir rigurosamente en este vídeo, nos proporcionará las herramientas necesarias para aplicar teoría de grupos complejos de coordinación simple y mostrar cómo puede utilizarse para predecir el número de modos vibracionales activos IR. Para demostrar, caminaremos a través de la aplicación de la teoría de grupos en la molécula cis -Mo(CO)4[P(OPh)3]2.
En primer lugar, debemos determinar el grupo de punto de la molécula. Grupos de puntos se utilizan para describir los elementos de simetría presentes en una molécula dada. Para determinar el grupo de punto de cis -Mo(CO)4[P(OPh)3]2, podemos usar un diagrama de flujo que se llama un árbol de simetría, que pide una serie de preguntas acerca de los elementos de simetría presentes en la molécula (figura 2). La tabla 1 resume todos los elementos de simetría en el árbol de la simetría. Usando el árbol de la simetría y suponiendo que los ligandos P(OPh)3 son punto de ligandos (ignorando al mismo tiempo la simetría de los ligandos), encontramos cis -Mo(CO)4[P(OPh)3]2 está en el grupo del punto C 2v.

Figura 2. Árbol de simetría utilizado para la determinación del punto de grupo.
Tabla 1. Elementos de simetría utilizan en el punto determinación de grupo.
| Elemento de simetría | Símbolo utilizado | Ejemplo * |
| Identidad | E |  |
| Eje de rotación (rotación de 360 ° /n) |
C n |  |
| Plano de espejo horizontal (reflexión sobre el plano xy) |
Σ h |  |
| Plano de espejo vertical (reflexión sobre el plano xz o yz) |
Σ v |  |
| Plano del espejo diagonal (reflexión entre planos xz y yz) |
Σ d |  |
| Centro de la inversión | me |  |
| Eje de rotación impropio (rotación de 360 /n ° seguido de reflexión perpendicular al eje de rotación) |
S n |  |
| * Los ejemplos son para un complejo octaédrico, donde ligandos 1–6 son equivalentes. Al efectuar la operación, la molécula resultante debe ser indistinguible de su configuración original. | ||
Para el siguiente paso, tenemos que introducir tablas de caracteres, que describen todas la simetría presente dentro de un grupo determinado. A continuación se muestra la tabla de caracteres para el punto grupo C2v .
| C 2v | E | C 2 | Σ v (xz) | Σ v ' (yz) | ||
| A 1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A 2 | 1 | 1 | −1 | −1 | Rz | XY |
| B 1 | 1 | −1 | 1 | −1 | x, Ry | XZ |
| B 2 | 1 | −1 | −1 | 1 | y, Rx | YZ |
El grupo punto se indica en la esquina superior izquierda de la tabla de caracteres. A la derecha del punto de grupo, se enumeran todas las operaciones de simetría inherentes a ese grupo de punto.Las filas posteriores la lista todas las representaciones de la simetría (las representaciones irreducibles, representadas por símbolos Mulliken, i.e.,A1) contenida en ese grupo de puntos, junto con la simetría de las funciones, que nos puede decir sobre la simetría de orbitales atómicos como movimiento lineal a lo largo de los ejes x, y y z.
Utilizando la tabla de caracteres para el punto grupo C2v, generar una representación reducible (Γrojo) de los modos de estiramiento C-oh en la molécula cis -Mo(CO)4[P(OPh)3]2 (figura 3 ). La representación reducible, o la combinación lineal de las representaciones irreducibles, puede ser generada por la aplicación de cada una de las operaciones de simetría en la tabla de caracteres a las vibraciones dentro de la molécula y registrar el número de vibraciones O C que permanecen inalterados (en la misma posición en el espacio). Por ejemplo, al aplicar el elemento de simetría de la identidad a las vibraciones de la C O en cis -Mo(CO)4[P(OPh)3]2, cuatro de las flechas vibracionales permanece en la misma posición. Por lo tanto, el primer valor de la representación reducible es 4. Si seguimos este ejercicio, se genera la representación reducible que se muestra a continuación.
| C 2v | E | C 2 | Σ v (xz) | Σ v ' (yz) |
| Γ rojo | 4 | 0 | 2 | 2 |
A continuación, utilizamos la tabla de caracteres C2v para encontrar la combinación lineal de las representaciones irreducibles que genera Γroja para las vibraciones de la C O en cis -Mo(CO)4[P(OPh)3]2. Reducción de la representación reducible puede lograrse utilizando la fórmula de reducción que se muestra en la ecuación 3.
 (3)
(3)
donde:
n = número de veces que la representación irreducible ocurre en la representación reducible
h = orden del grupo (número total de operaciones de simetría)
c = la clase de operación
gc = número de operaciones en la clase
Χ = carácter de la representación irreducible para las operaciones de la clase
Χ r = carácter de la representación reducible para las operaciones de la clase
Utilizando la ecuación 3 para cada una de las representaciones irreducibles en la tabla de caracteres C2v, encontramos que Γrojo = 2A1 + B1 + B2. Los tres de las representaciones irreducibles que contribuye, A1, B1y B2, son IR activo porque transforman como el x, y o eje z (ver la simetría de las funciones en el tabla de caracteres). Por lo tanto, podemos predecir que cis -Mo(CO)4[P(OPh)3]2 presenta 4 modos de estiramiento C O en su espectro IR.
Para resumir, los pasos siguientes son necesarios para determinar el número de modos vibracionales activos de IR en una molécula:
1. determinar el grupo de punto de la molécula.
2. generar una representación reducible de las vibraciones de estiramiento C O dentro de la molécula.
3. reducir la representación reducible mediante la ecuación 3.
4. identificar el número de representaciones irreducibles traslacionales presentes en la representación reducida del paso 3.
Siguiendo estos 4 pasos con trans -Mo(CO)4[P(OPh)3]2, encontramos que la molécula posee sólo 1 activo C-O modo vibracional.

Figura 3. CO vibracional se extiende en cis-Mo(CO)4[P(OPh)3]2.
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. configuración de la línea de Schlenk (para un procedimiento más detallado, por favor revisar el video "Schlenk líneas transferencia de disolvente" de la serie de fundamentos de química orgánica ). Seguridad de línea de Schlenk debe revisarse antes de realizar este experimento. Vidrio debe ser inspeccionado para estrellas grietas antes de su uso. Debe tenerse cuidado para asegurar que el O2 no se condensa en la trampa de la línea de Schlenk si utiliza líquido N2. Temperaturas líquido N2 , O2 se condensa y es explosivo en presencia de solventes orgánicos. Si se sospecha que ha sido condensado O2 o un líquido de color azul se observa en la trampa de frío, deje que la trampa fría bajo vacío dinámico. No retire el líquido N2 purgador o apagar la bomba de vacío. Con el tiempo el líquido O2 se sublime en la bomba; sólo es seguro remover la trampa de2 N líquida una vez de O2 ha sublimado.
- Cierre la válvula de liberación de presión.
- Encienda el gas de N2 y la bomba de vacío.
- Como el Schlenk línea vacío alcanza su presión mínima, preparar la trampa de frío con hielo seco/acetona o líquido N2 .
- Montar la trampa de frío.
2. síntesis de Mo(CO)4[P(OPh)3]2 (Figura 4)1
Nota: Utilizar técnicas de línea de Schlenk estándar para la síntesis de Mo(CO)4[P(OPh)3]2 (ver el video de "Síntesis de una línea de Schlenk de uso de metaloceno Ti(III) técnica"). Complejos de metal carbonilo son una fuente de CO libre, que es altamente tóxico. Intoxicación por monóxido de carbono se produce cuando el CO se une a la hemoglobina, resultando en una reducción significativa del suministro de oxígeno al cuerpo. Por lo tanto, es muy importante tomar medidas de seguridad apropiadas durante la manipulación y trabajo con complejos carbonilo de metal. Reacciones que generan CO libre deban llevarse a cabo en una campana bien ventilada para evitar la exposición al gas tóxico.
- Añadir 1,6 g (4.92 mmol) Mo(CO)4(nbd) (nbd = 2,5-p) y 1.6 mL (9.84 mmol) trifenil fosfito (P(OPh)3) a un matraz de 100 mL Schlenk y preparar el matraz Schlenk para la transferencia de la cánula de solvente.
Nota: Mo(CO)4(nbd) ((Bicyclo[2.2.1]hepta-2,5-diene)tetracarbonylmolybdenum(0)) pueden comprarse en Sigma Aldrich o sintetizado usando métodos de la literatura. 2 - Añadir 20 mL de diclorometano desgasificada al matraz Schlenk vía transferencia de la cánula.
- Revuelva la mezcla de reacción durante 4 h a temperatura ambiente bajo N2.
- Eliminar los volátiles bajo vacío y el resultante lavado precipitan con frío hexanes (dos lavados con 10 mL, 78 ° C).
- Secar el sólido producto bajo vacío durante 15 minutos.
- Medir el espectro IR del producto en una solución de hexanes.

Figura 4. Síntesis de Mo(CO)4[P(OPh)3]2.
Teoría de grupos es un modelo matemático conectarse Simetría molecular de propiedades como modos vibracionales activos en el IR.
Cada molécula puede ser clasificado con un punto el grupo, que describe cada elemento de simetría presentes en una molécula con respecto a un punto fijo.
Teoría de grupos proporciona tablas especiales, llamadas tablas de caracteres, para predecir el efecto de la simetría de la molécula en sus modos de vibración y otras propiedades importantes.
Este video será discutir los principios de teoría del grupo, ilustran el procedimiento para la síntesis y caracterización de un isómero de Mo(CO)4[P(OPh)3]2e introducir algunas aplicaciones de teoría del grupo en química.
Simetría molecular describe las configuraciones indistinguibles de una molécula. Las transformaciones entre ellos se llaman operaciones de simetría, que se producen con respecto a uno o más elementos de la simetría.
Los cinco elementos de simetría son ejes de rotación adecuada e inadecuada, espejo planos, centros de inversión y la identidad. Cada molécula tiene el elemento de identidad , o E, en que se produzca ningún cambio .
Un plano espejo, etiquetado σ, es un plano de reflexión con iguales empezando y terminando las configuraciones. Las moléculas pueden tener más de un plano de espejo. Un centro de inversión, con la etiqueta , es un punto a través del cual se refleja cada átomo.
Un eje de rotación apropiado es un eje alrededor del cual gira una molécula a una configuración idéntica. Tiene el rótulo Cn, donde n es 360 dividido por el ángulo de rotación.
Un eje de rotación impropio , etiquetado Sn, es el eje alrededor de que una molécula es rotada y reflejado a través de un plano perpendicular espejo. Las moléculas pueden tener más de un eje de rotación. El eje con el más alto n es el eje principal.
Moléculas se asignan a grupos con un árbol de simetría, que identifica las operaciones de la simetría necesarias para clasificar la molécula.
Por ejemplo, BF3 es no lineal. Lo hace no tiene por lo menos dos ejes con n mayor que 2. Tiene al menos un eje de rotación; su eje principal es C3. Tiene tres C2 ejes perpendiculares a su eje principal y un plano espejo perpendicular a su eje principal. Así, trifluoruro de boro pertenece al grupo de punto de3 h de D.
Cada grupo de puntos tiene una tabla de caracteres sus operaciones de simetría esencial. Cada fila contiene una representación irreducible de las operaciones, junto con los correspondientes orbitales atómicos y movimientos lineales.
Representaciones reducibles se generan mediante la evaluación de cómo afectan a las operaciones de simetría propiedades moleculares. Reducción esta representación da las representaciones irreducibles que contribuye.
Ahora que usted comprende los principios de la teoría del grupo, vamos a ir a través de un procedimiento para sintetizar un isómero de Mo(CO)4[P(OPh)3]2 y la comparación de su espectro de IR en el número de modos activos en el IR predicen para cada isómero de Teoría de grupos.
Para comenzar el procedimiento, cierre la ventilación de la línea de Schlenk y empezar el flujo de gas de2 N.
En una campana de humos, mida 0.5 g de Mo(CO)4(nbd) y coloque el precursor de molibdeno en un matraz Schlenk de 200 mL. Equipar el matraz de reacción con una barra de agitación y tapar el matraz con un tapón de vidrio. Conectar el matraz a la línea de Schlenk vía el brazo del lado, y preparar el frasco para la cánula de transferencia por evacuar el recipiente por 5 minutos, seguido por rellenar el frasco con N2. Repita esta evacuación y recarga el proceso un total de 3 veces.
A continuación, preparar otro matraz Schlenk con una membrana de goma que contiene 20 mL de CH2Cl2. Conectar el matraz a la línea de Schlenk y asegure el matraz en la campana. Utilizando una jeringa, elaborar 0,87 mL de trifenil fosfito y dispensar en el matraz Schlenk. Asegúrese de que la llave de paso línea de Schlenk es N2. Desgasificar el CH2Cl2/triphenyl mezcla de fosfito por burbujas de N2 por el solvente durante 10 minutos. Luego use transferencia de cánula para añadir la solución al matraz que contiene el sólido. Abra el frasco de reacción a gas de2 N y agitar la mezcla a temperatura ambiente durante 4 horas.
Una vez terminada la reacción, vuelva a colocar la membrana de goma con un tapón de vidrio y remover los solventes volátiles bajo vacío.
Añadir hexanes al producto resultante y enfriar en un baño de hielo seco/acetona brevemente, hasta que un precipitado formas. Filtrar el precipitado y lavar el precipitado dos veces con 10 mL de hexanes frío y recoger el sólido por filtración. Secar el sólido producto bajo vacío durante 15 minutos.
Por último, disolver una porción del producto en hexanes y cargar la solución en una célula de IR. Adquirir un espectro de IR del complejo.
Ahora, vamos a determinar si el producto es cis o trans isómero asignando señalan grupos de ambos isómeros y la comparación de los modos previstos de activos en el IR para el espectro IR.
El cis ni trans isómero es lineal y tampoco tiene más de dos ejes de rotación con órdenes superiores a 2. Ambos tienen al menos un eje de rotación. Los ejes principales para los isómeros cis y trans son C2 y C4, respectivamente.
El isómero cis tiene dos C2 ejes perpendiculares a su eje de2 C, ni tiene un plano espejo perpendicular. Tiene dos planos del espejo que contiene el eje de2 C, por lo que su grupo del punto es C2v. El isómero trans tiene cuatro C2 ejes y un plano espejo perpendicular a su eje de4 C, por lo que su grupo del punto es D4 h.
Representaciones reducibles, próximo de los tramos de CO se generan aplicando cada operación de simetría para la molécula y contando los tramos C-O que no cambian de ubicación en el espacio.
La tabla de2v Ctiene cuatro operaciones: identidad, C2 rotación y reflexiones a través de dos planos espejo que contiene el eje de2 C. En la operación de identidad, todos los momentos de dipolo cuatro siguen vigentes. Los cuatro momentos de dipolo tomar posiciones después de una rotación de2 C. Dos momentos de dipolo permanecen en la misma posición para cada reflexión.
La fórmula de reducción calcula el coeficiente de cada representación irreducible en la representación reducible. El grupo de punto de orden es el número de operaciones de simetría. Las clases son tipos de operaciones de simetría. Aquí, el número de operaciones en cada clase es de 1, que tradicionalmente se omite de una tabla de caracteres.
El carácter es el valor correspondiente a una representación de una clase dada. Cuando se aplica la fórmula de reducción, se encuentran tres representaciones irreducibles, con uno que ocurre dos veces. Estas representaciones se transforman como eje de las x, yo z , que es coherente con cuatro tramos de activos en el IR C-O.
Utilizando la misma técnica, el isómero trans es encontrado para tener un tramo de IR activo C-O. El espectro IR del producto molibdeno tiene picos en 1942, 1958 y 2046 cm-1. Con datos de mayor resolución, se puede observar un cuarto tramo de la C-O. Partiendo de la IR obtenida, se puede concluir que el aislado Mo(CO)4[P(OPh)3]2 complejo es el isómero cis .
Teoría de grupos es ampliamente utilizado en química orgánica e inorgánica. Echemos un vistazo a algunos ejemplos.
Espectroscopía Raman detecta vibraciones moleculares que implican cambios en la polarizabilidad de la nube de electrones. Un estiramiento simétrico en CO2 no cambia el momento de dipolo y por lo tanto no activos en el IR. Sin embargo, alejarse de los núcleos de electrones cambian la polarizabilidad, haciendo el tramo Raman activo. Teoría del grupo puede identificar modos vibracionales Raman activo siguiendo el mismo método general usado para identificar modos de activos en el IR.
Teoría orbital molecular o teoría de MO, es un modelo utilizado para describir el enlace en las moléculas. Sumando y restando los orbitarios atómicos de dos átomos conduce a la formación de diagramas de orbitales moleculares de diatomics simple.
Para generar diagramas de MO de complejos de metales de transición, los científicos utilizan la teoría de grupos para generar combinaciones lineales adaptados simetría de orbitales atómicos para representar los átomos exteriores o ligandos. Esto se logra generando representaciones reducibles de los orbitarios atómicos del ligand, y luego reducir esto a una representación irreducible.
Se comparan las representaciones de la simetría de centro metálico y las combinaciones lineales adaptados simetría en el diagrama. En este modelo, los orbitales con la misma simetría se solapaban en forma dos orbitales moleculares.
Sólo ha visto la introducción de Zeus a teoría del grupo. Ahora debe familiarizarse con los principios fundamentales de simetría molecular, encontrando el grupo de punto de una molécula y algunos ejemplos de cómo la teoría de grupos se utiliza en química orgánica e inorgánica. ¡Gracias por ver!
Subscription Required. Please recommend JoVE to your librarian.
Results

Figura 5. IR de Mo(CO)4[P(OPh)3]2.
Solución IR en hidrocarburos saturados (cm-1): 2046 (s), 1958 (s), 1942 (vs).
La cuarta resonancia puede verse sólo bajo condiciones de alta resolución. Por lo tanto, es posible, como en este caso, que sólo 3 de las 4 resonancias se observan.
Basado en lo IR obtenido, podemos concluir que cis-isómero de Mo(CO)4[P(OPh)3]2 fue aislado.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
En este video, aprendimos a utilizar teoría de grupos para predecir el número de modos vibracionales activos de IR en una molécula. Había sintetizado la molécula Mo(CO)4[P(OPh)3]2 y usa IR para determinar qué isómero aislado. Observamos que el producto tenía tres vibraciones de la C O en su espectro de IR, que es consistente con el cis-isómero.
Teoría de grupos es una poderosa herramienta que es usada por los químicos predecir no sólo modos vibracionales activos IR, pero también vibracional, rotacional y otros modos de baja frecuencia en espectroscopia de Raman. Además, teoría de grupos se aplica en teoría (MO) orbital molecular, que es el modelo más ampliamente utilizado para describir la vinculación dentro de complejos de metales de transición. Diagramas de MO, utilizadas por químicos orgánicos e inorgánicos, pueden predecir y explicar la reactividad observada de la molécula.
1st, 2ndy 3rd fila metal carbonilo complejos se utilizan ampliamente en síntesis inorgánica como precursores metálicos para compuestos organometálicos más complejos. Algunos de los tipos más comunes de reacciones con complejos carbonilo de metal incluyen sustitución de ligando CO redox en el centro de metal y ataque nucleofílico en la unidad de CO. Carbonilo de metal complejos se utilizan ampliamente en catálisis. Por ejemplo, hidroformilación, la producción industrial de aldehídos de los alkenes, es catalizada por metal carbonilo complejo HCo(CO)3 (figura 6).

Figura 6. Hidroformilación por el carbonilo de metal complejo HCo(CO)3.
Subscription Required. Please recommend JoVE to your librarian.
References
- Fukumoto, K., Nakazawa, H. Geometrical isomerization of fac/mer-Mo(CO)3(phosphite)3 and cis/trans-Mo(CO)4(phosphite)2 catalyzed by Me3SiOSO2CF3. J Organomet Chem. 693(11), 1968-1974 (2008).
- Darensbourg, M. Y., Magdalena, P., Houliston, S. A., Kidwell, K. P., Spencer, D., Chojnacki, S. S., Reibenspies, J. H. Stereochemical nonrigidity in heterobimetallic complexes containing the bent metallocene-thiolate fragment. Inorg Chem. 31(8), 1487-1493 (1992).
- Darensbourg, M. Y., Darensbourg, D. J. Infrared Determination of Stereochemistry in Metal Complexes. J Chem Ed. 47(1), 33-35 (1970).




