Overview
Quelle: Labor von Dr. Andreas Züttel - schweizerischen Eidgenössischen Laboratorien für Werkstoffwissenschaft und Werkstofftechnologie
Das ideale Gasgesetz beschreibt das Verhalten der am häufigsten verwendeten Gase bei in der Nähe-Umgebungsbedingungen und die Tendenz aller chemischen Materie in der verdünnten zu begrenzen. Es ist eine grundlegende Beziehung zwischen drei messbare makroskopischen Systemvariablen (Druck, Temperatur und Volumen) und die Anzahl der Moleküle des Gases in das System und ist somit ein wichtiges Bindeglied zwischen der mikroskopischen und makroskopischen Universen.
Die Geschichte des idealen Gases Gesetzes reicht bis zur Mitte des17. Jahrhunderts als das Verhältnis zwischen Druck und Volumen der Luft gefunden wurde, umgekehrt proportional, ein Ausdruck von Robert Boyle und die wir jetzt als Boyles Gesetz (Gleichung 1) bezeichnen bestätigt .
P 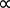 V-1 (Gleichung 1)
V-1 (Gleichung 1)
Unveröffentlichte Arbeit von Jacques Charles in den 1780er Jahren, das wurde erweitert, um zahlreiche Gase und Dämpfe von Joseph Louis Gay-Lussac und berichtet im Jahre 1802, gegründet direkt proportionale Beziehung zwischen der absoluten Temperatur und Volumen eines Gases. Diese Beziehung ist Karls Gesetz (Gleichung 2) genannt.
V 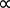 T (Gleichung 2)
T (Gleichung 2)
Guillaume Amontons ist in der Regel mit der ersten Entdeckung der Beziehung zwischen der Temperatur und der Druck der Luft in einem festen Volumen an der Wende des18. Jahrhunderts gutgeschrieben. Dieses Gesetz wurde auch auf zahlreiche andere Gase durch Joseph Louis Gay-Lussac zu Beginn des19. Jahrhunderts erweitert und ist somit entweder als entweder Amontonss oder Gay-Lussac-Gesetz, erklärt wie in Gleichung 3bezeichnet.
P 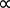 T (Gleichung 3)
T (Gleichung 3)
Gemeinsam können diese drei Beziehungen kombiniert werden, um die Beziehung in Gleichung 4geben.
V 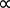 T (Gleichung 4)
T (Gleichung 4)
Schließlich wurde im Jahr 1811 von Amedeo Avogadro vorgeschlagen, dass keine zwei Gase, gehalten in der gleichen Lautstärke und bei der gleichen Temperatur und Druck, die gleiche Anzahl von Molekülen enthalten. Dies führte zu dem Schluss, dass alle Gase durch eine gemeinsame Konstante, die ideale Gaskonstante R, beschrieben werden können, die unabhängig von der Beschaffenheit des Gases ist. Dies nennt man das ideale Gasgesetz (Gleichung 5). 1,2
PV 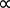 T (Gleichung 5)
T (Gleichung 5)
Principles
Das ideale Gasgesetz und damit seine charakteristische konstante R auch eloquent aus ersten Prinzipien Theorie auf vielfältige Weise ableiten wo die wichtigen vereinfachenden Annahmen sind, dass die Moleküle keine inhärente Volumen haben und nicht interagieren. Diese Annahmen gelten in der verdünnten Angelegenheit zu begrenzen, wo das Volumen der leere Raum für jedes Molekül (z. B. ~ 10-23 L bei Umgebungsbedingungen) ist viel größer als das Molekül selbst (~ 10-26 L) und Wechselwirkungen unwahrscheinlich sind. Es kann daher leicht in eine Reihe von Möglichkeiten, mit gemeinsamen Laborgeräte bei Raumtemperatur nachgewiesen werden, und kann mit einer Vielzahl von Gasen bei Drücken bis zu sogar 10 genau gemessen werden (Abbildung 1). Allerdings kann nicht das ideale Gasgesetz genau ausmachen, für die Eigenschaften der Dichter Gase bei in der Nähe-Umgebungsbedingungen (z.B. Propan) oder für die Kondensation, Phänomene, die durch intermolekulare Wechselwirkungen entstehen. Aus diesem Grund gelungen, zahlreiche detaillierte Zustandsgleichungen das ideale Gasgesetz in den Jahren seit seiner Entdeckung, in der Regel auf das ideale Gasgesetz in der verdünnten Angelegenheit zu begrenzen zu reduzieren. 1,2

Abbildung 1. Vergleich der idealen Gases Recht Dichte zu verschiedenen anderen gemeinsamen Gasen bei 25 ° C und zwischen 0-100 Bar.
In diesem Tutorial, messen wir sorgfältig die Dichte von Wasserstoffgas bei erhöhten Drücken und Temperaturen in einem festen Volumen durch wiegen einer schwebenden festen Probe von bekanntem Volumen: eine präzise gefräste Aluminium-Block. Die Änderung im Gewicht der Probe bezieht sich direkt auf die Änderung in Flüssigkeitsdichte, in der er schwebt, von Archimedes Prinzip. Wir zeigen auch die Mängel der Verwendung einer weniger idealen Gases (z.B. Kohlendioxid) bei hohen drücken. Zu guter Letzt wir visuell demonstrieren und qualitativ bestätigen das ideale Gasgesetz durch Ausführen einer einfachen Benchtop-Experiments wo wird die Änderung im Volumen des Systems durch Wasserstoff-Freisetzung durch eine Wasserstoff-Speichermaterial gemessen. Unter Verwendung einer dieser Experimente, können wir die Naturkonstante bestimmen, die die Beziehung zwischen Druck, Temperatur und Volumen für eine gegebene Menge von Gas – die ideale Gaskonstante R. beschreibt
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. Messung des Volumens der Probe
- Die Probe sorgfältig reinigen und trocknen.
- Füllen Sie eine hochauflösende Messzylinder mit genug destilliertes Wasser auf die Probe zu decken. Beachten Sie die Ausgangsmenge
- Ziehen Sie das Sample in das Wasser, und beachten Sie die Volumenänderung. Dies ist das Volumen der Probe, V.
- Entfernen Sie die Probe und trocknen. Hinweis: Alternativ Seite Länge(n) der Probe gemessen und sein Volumen mit Geometrie zu berechnen.
2. Legen Sie die Probe in der Schwebe
- Hängen Sie die Probe in der Schwebe magnetischer Aufhängung.
- Die Druck/Temperatur-Kammer um die Probe zu installieren.
- Evakuieren Sie die Probenumgebung zu und füllen Sie mit Wasserstoffgas, bis 1 Bar.
- Messen Sie das Gewicht der Probe auf 1 Bar und Raumtemperatur, w00.
(3) Maßnahme Probengewicht als Funktion des Drucks bei Raumtemperatur
- Erhöhen Sie oder verringern Sie den Druck in der Probenumgebung um Pi0.
- Die Probenumgebung zu equilibrate zu ermöglichen.
- Messen Sie das Gewicht der Probe, wi0.
- 3.1-3.3 mehrmals zu wiederholen.
4. Messen Sie Probengewicht als Funktion des Drucks bei verschiedenen Temperaturen
- Stellen Sie die Temperatur Tj und lassen Sie ihn equilibrate.
- Stellen Sie den Druck des Wasserstoffgases bis 1 Bar.
- Messen Sie das Gewicht der Probe auf 1 Bar und Tj, w0j.
- Erhöhen Sie oder verringern Sie den Druck auf PIj und lassen Sie ihn equilibrate.
- Messen Sie das Gewicht der Probe, wIj.
- 4,4-4,5 mehrmals zu wiederholen.
- Wiederholen Sie 4.1-4.6 wie gewünscht.
5. berechnen Sie die ideale Gaskonstante
- Tabellieren Sie die gemessenen Werte {Tj, PIjund wIj} wo P0j ist immer 1 Bar und T0 ist die gemessene Raumtemperatur.
- Berechnen Sie und Tabellieren Sie die Unterschiede ΔwIj und ΔPIj bei jeder Temperatur Tj mit Gleichung 6 und 7 der Gleichung.
ΔwIj = wIj - w0j (Gleichung 6)
ΔwIj = PIj - P0j = PIj - 1 bar (Gleichung 7) - Berechnen Sie RIj für jede Messung und Durchschnitt aller Werte zu bestimmen, die ideale Gaskonstante, R. Alternativ zeichnen das Produkt aus ΔPIj und V als Funktion des Produkts ΔwIj (dividiert durch das Molekulargewicht MW) und T-j, und führen Sie eine lineare Regression-Analyse zur Ermittlung der Steigung, R. (Gleichungen 8 und 9) für Wasserstoff , MW = 2.016 g/Mol.
ΔP V = Δn RT (Gleichung 8)
 (Gleichung 9)
(Gleichung 9)
Das ideale Gasgesetz ist eine grundlegende und nützliche Beziehung in der Wissenschaft, wie es das Verhalten der am häufigsten verwendeten Gase bei in der Nähe-Umgebungsbedingungen beschreibt.
Das ideale Gasgesetz, PV = nRT, definiert die Beziehung zwischen der Anzahl der Moleküle des Gases in einem geschlossenen System und drei messbare Systemvariablen: Druck, Temperatur und Volumen.
Das ideale Gasgesetz aus ersten Prinzipien ableiten beruht auf zwei Annahmen. Erstens, dass die Gasmoleküle selbst kein Volumen haben. Zweitens: die Moleküle nie interagieren oder Austausch von Energie. Gasen abweichen von diesem idealen Verhalten bei hohen Drücken, wo der gasdichte erhöht, und die reale Volumen der Gasmoleküle gewinnt an Bedeutung. In ähnlicher Weise abweichen Gase bei extrem niedrigen Temperaturen, wo attraktive intermolekulare Wechselwirkungen an Bedeutung gewonnen. Schwerere Gase können auch bei Raumtemperatur und Druck aufgrund ihrer höheren Dichte und stärkeren intermolekularen Wechselwirkungen abweichen.
Dieses Video wird das ideale Gasgesetz experimentell bestätigen, durch Messung der Veränderung der Dichte eines Gases in Abhängigkeit von Temperatur und Druck.
Das ideale Gasgesetz wird von vier wichtigen Beziehungen abgeleitet. Boyles Gesetz beschreibt zunächst die umgekehrt proportionale Beziehung zwischen Druck und Volumen eines Gases. Als nächstes bestimmt Gay-Lussac Gesetz, dass Temperatur und Druck proportional sind. Ebenso ist Karls Gesetz eine Aussage über die Verhältnismäßigkeit zwischen Temperatur und Wassermenge. Diese drei Beziehungen bilden das kombinierte Gasgesetz, das den Vergleich eines einzelnen Gases über viele verschiedene Bedingungen ermöglicht.
Schließlich festgestellt Avogadro, dass keine zwei Gase, bei gleichem Volumen, Temperatur und Druck, statt die gleiche Anzahl von Molekülen enthalten. Da Gase unter der gleichen Bedingung in der Regel das gleiche Verhalten, konnte eine Konstante der Verhältnismäßigkeit, die allgemeine Gaskonstante (R), rief gefunden werden, diese Parameter ermöglichen den Vergleich verschiedener Gase beziehen. R hat Maßeinheiten von Energie pro Temperatur pro Molekül; zum Beispiel, Joule pro Kelvin pro Mol.
Das ideale Gasgesetz ist ein wertvolles Werkzeug in staatlichen Beziehungen in gasförmigen Systemen zu verstehen. Beispielsweise führt die Zugabe von mehr Gasmoleküle in einem System von konstanter Temperatur und Druck, erhöhte Volumen.
Ebenso wird bei konstanter Temperatur in einem geschlossenen System, wo keine Moleküle addiert oder subtrahiert werden, der Druck eines Gases erhöht Volumen verringert wird.
Ein magnetischer Aufhängung Gleichgewicht kann verwendet werden, um das ideale Gasgesetz experimentell zu bestätigen, durch die Messung der physikalischen Eigenschaften eines Systems. Das Gewicht einer festen Probe konstanten Masse und Volumen dient als eine Sonde der Eigenschaften des Gases um ihn herum.
Zunehmender Druck im System bei konstante Systemvolume und Temperatur, erhöht die Menge der Gasmoleküle im System, wodurch der Gasdichte. Die starren feste Probe eingetaucht in dieses Gas unterliegt Auftrieb, und seine scheinbare Gewicht sinkt, obwohl seine Masse unverändert ist. Die Veränderung der gasdichte kann wegen Archimedes Prinzip ermittelt werden, die besagt, dass die Änderung im Objekt Gewicht gleich die Änderung im Gewicht des Gases, die verdrängt wird.
Die genaue Verhalten der gasdichte unter verschiedenen Druck- und Temperaturbedingungen werden das ideale Gasgesetz entsprechen, wenn sich die zuvor beschriebenen Annäherungen, ermöglicht die einfache Berechnung der allgemeine Gaskonstante, R.
In der folgenden Serie von Experimenten dienen einer Mikrowaage bestätigen das ideale Gasgesetz und die allgemeine Gaskonstante R, durch Messung der Dichte des Wasserstoffs als Funktion der Temperatur und des Drucks zu bestimmen. Zuerst sorgfältig reinigen Sie die Probe, in diesem Fall ein fein bearbeiteten Aluminium-Block, mit Aceton und trocknen Sie. Messen Sie das Volumen der Probe durch das Ausfüllen eines abgestuften Zylinder mit genug destilliertes Wasser auf die Probe zu decken. Beachten Sie das Ausgangsvolumen. Tauchen Sie die Probe in das Wasser, und beachten Sie die Volumenänderung.
Entfernen Sie und vorsichtig reinigen Sie und trocknen Sie die Probe. Als nächstes laden Sie sie in das magnetischer Aufhängung Gleichgewicht, in diesem Fall befindet sich im Inneren ein Handschuhfach. Installieren Sie die Druck-Temperatur-Kammer um die Probe. Die Probe ist nun magnetisch ausgesetzt, in einem geschlossenen System, keine der Wände zu berühren.
Evakuieren Sie die Probenumgebung zu und füllen Sie mit Wasserstoff bei einem Druck von 1 Bar.
Messen Sie das Gewicht der Probe zu, und bezeichnen Sie es als das Ausgangsgewicht bei Raumtemperatur. Danach erhöhen Sie den Druck in der Probenumgebung auf 2 Bar und lassen Sie es equilibrate. Das Gewicht auf den neuen Druck zu messen. Wiederholen Sie diese Schritte mehrmals an einer Reihe von Belastungen, eine Reihe von Einwaagen bei entsprechenden Druck, alle bei Raumtemperatur zu erwerben.
Als nächstes messen Sie Gewicht als Funktion des Drucks bei einer höheren Temperatur. Zuerst evakuieren Sie die Probenumgebung, dann erhöhen Sie die Temperatur auf 150 ° C und lassen Sie es zu equilibrate. Dann erhöhen Sie den Druck bis 1 Bar. Messen Sie das Gewicht der Probe zu, und bezeichnen Sie es als das Ausgangsgewicht bei 150 ° C und 1 Bar. Erhöhen Sie den Druck, lassen Sie es zu equilibrate und Messen Sie das Gewicht. Wiederholen Sie diese Schritte, um eine Reihe von Einwaagen auf eine Reihe von Druck zu messen. Um mehr Daten zu erhalten, wiederholen Sie die Reihe der Gewichtsmessung bei anderen konstanten Temperaturen und drücke.
Um die ideale Gaskonstante berechnen, Tabellieren Sie die gemessenen Werte der Einwaage bei jeder Temperatur und Druck.
Als Nächstes berechnen Sie die Unterschiede zwischen allen Paaren von Einwaagen innerhalb einer einzelnen Temperatur eingestellt, alle mögliche Kombinationen der Änderung im Gewicht als Funktion der Änderung in Druck oder Δw zu erhalten. Diese Änderung ist gleichbedeutend mit der Änderung im Gewicht von Wasserstoffgas, das durch die Probe verdrängt wird.
In ähnlicher Weise berechnen Sie alle entsprechenden Druckunterschiede Änderung in Druck oder ΔP zu erhalten. Tabellieren Sie alle Paare von Veränderungen in Gewicht und Druck für jede Temperatur. Konvertieren Sie die Einheiten der Temperatur in Kelvin und die Einheiten des Drucks auf Pascals.
Da das Volumen und die Temperatur für jede Serie von Messungen konstant bleiben, das ideale Gasgesetz kann als ΔPV geschrieben werden = ΔnRT. Da Δn Δw geteilt durch das Molekulargewicht von Wasserstoff entspricht, berechnen Sie jeden Wert des Δn für jeden Wert des Δw.
Plot-das Produkt der Druckänderung und probieren Sie Volumen, als eine Funktion des Produkts von Δn und Temperatur. Führen Sie eine lineare Regression-Analyse, um die Steigung zu bestimmen, die welche die allgemeine Gaskonstante gleich wird, wenn es richtig gemacht.
Die Ideale Gasgleichung dient in vielen realen Szenarien, typischerweise diejenigen, die mit Gasen bei Umgebungstemperatur und Druck durchgeführt. Alle Gase abweichen vom idealen Verhalten unter hohem Druck; jedoch weichen einige Gase wie Kohlendioxid, mehr als andere. In diesem Experiment wurden Abweichungen vom idealen Verhalten für Kohlendioxid gemessen. Das Verfahren war identisch mit dem vorherigen Experiment durchgeführt mit Wasserstoff.
Ein Grundstück von Druck mal Volumen gegen die Maulwürfe Mal Temperatur aufgetragen wurde, und die ideale Gaskonstante aus der Neigung des Grundstücks berechnet. Kohlendioxid wich deutlich von ideales Verhalten, auch bei Umgebungsbedingungen. Dieses Verhalten wurde durch attraktiven intermolekularen Wechselwirkungen verursacht, die nicht mit Wasserstoff zu beobachten war.
Das ideale Gasgesetz dient der Identifizierung und Quantifizierung von explosiven Gasen in Luftproben. Dieses Forschungsgebiet ist extrem wichtig für das Militär und Sicherheit.
Hier wurden explosive Bestandteil einer Gasprobe quantifiziert mit Temperatur Desorption Gaschromatographie. Die Daten sowie das ideale Gasgesetz wurden dann verwendet, um diese gefährlichen Stoffe zu quantifizieren.
Sie habe nur Jupiters Einführung in das ideale Gasgesetz beobachtet. Nachdem ich dieses Video, sollten Sie verstehen, das Konzept des Gesetzes, und Situationen, wo die Gleichung gilt.
Danke fürs Zuschauen!
Subscription Required. Please recommend JoVE to your librarian.
Results
Das ideale Gasgesetz ist eine gültige Beschreibung der tatsächlichen Gas Eigenschaften der zahlreichen gemeinsamen Gase zu Konditionen in der Nähe von ambient (Abbildung 1 Einschub) und eignet sich daher im Zusammenhang mit vielen Anwendungen. Die Grenzen des idealen Gases Gesetzes beschreibt Systeme unter den Bedingungen der hohen Drücke oder niedrigen Temperaturen lässt sich durch die zunehmende Bedeutung der molekularen Wechselwirkungen und/oder die endliche Größe der Gasmoleküle, die einen Beitrag zu den Systemeigenschaften. Daher werden Gase mit starken, attraktiven intermolekularen Wechselwirkungen (aufgrund von Dipol-Dipol-Wechselwirkungen, einschließlich Wasserstoff-Bindung, Ion-Dipol-Wechselwirkungen oder van der Waals Wechselwirkungen) höhere dichten als ideales Gas aufweisen. Alle Gase haben auch eine abstoßende Komponente bei hohen dichten, da mehr als ein Molekül kann nicht am ursprünglichen Speicherort, Kreditvergabe eine Abnahme der Dichte über den idealen Gases zu besetzen. Gase wie Wasserstoff und Helium mehr maßgeblich von den abstoßend zeigen aufgrund der endlichen Molekülgröße erzwingen, und haben daher etwas niedriger Dichte bei hohen drücken. Methan und Kohlendioxid weitaus größere Beiträge anzeigen, deren Eigenschaften von attraktiven Interaktionen, verleihen ihnen höhere dichten als ideales Gas bis sehr hohe Drücke, wo der abstoßende Begriff dominiert (bei sehr viel höher als 100 Bar bei 25 ° C).

Abbildung 2. Gleichgewicht Adsorption Aufnahme Isotherme CO2 auf hohe Fläche, superactivated Kohlenstoff MSC-30, bei 25 ° C.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
Das ideale Gasgesetz ist solch eine Fundamentalgleichung der chemischen Wissenschaften, dass es eine Fülle von Anwendungen sowohl in Berechnungen als auch im täglichen Labortätigkeiten und Modellierung selbst hochkomplexe Systeme, zumindest in erster Näherung. Ihre Anwendbarkeit ist nur durch die inhärente Annäherungen an das Gesetz selbst beschränkt; in der Nähe von ambient Drücke und Temperaturen, wo das ideale Gasgesetz gut für viele gemeinsame Gase gilt, ist es weit verbreitet in der Interpretation von Gas-basierten Systemen und Prozessen eingesetzt. Zwei Beispiele für Geräte, die auf Prinzipien, die versöhnt werden können durch das ideale Gasgesetz nutzen, sind die Gas-Thermometer und der Stirlingmotor.
Eine bestimmte Anwendung ist bei der Messung der Menge an Gas Adsorption (Physisorption) auf der Oberfläche eines festen Materials. Adsorption ist das physikalische Phänomen, wobei Gasmoleküle die Gasphase zu verlassen und betreten Sie eine verdichtete Phase nahe der Oberfläche von festem Untergrund (oder vielleicht eine Flüssigkeit) aufgrund der attraktiven intermolekularen Wechselwirkungen (Zerstreuung Kräfte) zwischen der festen und das Gas. Die Rolle der Adsorption kann für viele lose Materialien (wie z.B. Glas und Edelstahl) Stahl bei Umgebungsbedingungen vernachlässigt werden, sondern wird sehr wichtig für poröse Materialien mit einer großen zugängliche Fläche, besonders bei niedrigen Temperaturen. 3 die volumetrische Sieverts Methode und die gravimetrische Methode zur Quantifizierung der physikalischen Adsorption Vertrauen auf wissen die Zustandsgleichung des Gases in das System. Bei niedrigem Druck und Umgebungstemperatur das ideale Gasgesetz gilt für viele Gase, und kann verwendet werden, um genau die adsorbierten Menge des Gases in ähnlicher Weise zu bestimmen, wie im Protokoll zur Ermittlung R oben beschrieben. Beispielsweise kann bei gravimetrischen Messungen dem Auftriebskörper aus einem hoch-Oberfläche-sorbent unter Bedingungen, wo die idealen Gases Gesetz tatsächlich gültig ist, die Differenz zwischen dertatsächlichen Δw gemessen, und Δwideale berechnet unter Verwendung der ideale Zustandsgleichung die Änderung im Gewicht der adsorbierten Phase zugeschrieben werden. (Gleichung 10) Gas Adsorption isothermen Gleichgewicht können somit durch Tabellieren dieser Abweichungen, ΔwAnzeigen, als Funktion des Drucks bei einer festen Temperatur gemessen werden (siehe Abbildung 2), ein Standardverfahren in der Charakterisierung von porösen Materialien.
ΔwAnzeigen = Δwtatsächliche - Δwideal (Gleichung 10)
Subscription Required. Please recommend JoVE to your librarian.
References
- Zumdahl, S.S., Chemical Principles. Houghton Mifflin, New York, NY. (2002).
- Kotz, J., Treichel, P., Townsend, J. Chemistry and Chemical Reactivity. 8th ed. Brooks/Cole, Belmont, CA (2012).
- Rouquerol, F., Rouquerol, J., Sing, K.S.W., Llewellyn, P., Maurin, G. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications.Academic Press, San Diego, CA. (2014).





 (Gleichung 9)
(Gleichung 9)