Overview
Source: Alexander S Rattner and Mahdi Nabil; Department of Mechanical and Nuclear Engineering, The Pennsylvania State University, University Park, PA
When liquid flows along an open channel at high velocity, the flow can become unstable, and slight disturbances can cause the liquid upper surface to transition abruptly to a higher level (Fig. 1a). This sharp increase in the liquid level is called a hydraulic jump. The increase in the liquid level causes a reduction in the average flow velocity. As a result, potentially destructive fluid kinetic energy is dissipated as heat. Hydraulic jumps are purposely engineered into large water works, such as dam spillways, to prevent damage and reduce erosion that could be caused by fast moving streams. Hydraulic jumps also occur naturally in rivers and streams, and can be observed in household conditions, such as the radial outflow of water from a faucet onto a sink (Fig. 1b).
In this project, an open-channel flow experimental facility will be constructed. A sluice gate will be installed, which is a vertical gate that can be raised or lowered to control the discharge rate of water from an upstream reservoir to a downstream spillway. The flow rate required to produce hydraulic jumps at the gate outlet will be measured. These findings will be compared with theoretical values based on mass and momentum analyses.
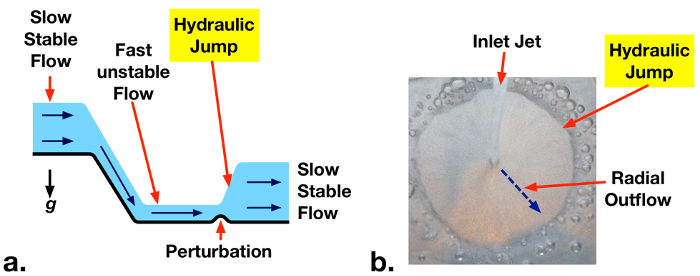
Figure 1: a. Hydraulic jump occurring downstream from a spillway due to a slight perturbation to an unstable high-velocity flow. b. Example of hydraulic jump in radial outflow of water from a household faucet.
Principles
In wide open-channel flows, liquid is only confined by a lower solid boundary and its upper surface is exposed to the atmosphere. A control-volume analysis can be performed on a section of an open channel flow to balance inlet and outlet transport of mass and momentum (Fig 2). If the velocities are assumed uniform at the inlet and outlet of the control volume (V1 and V2 respectively) with corresponding liquid depths H1 and H2, then a steady mass flow balance reduces to:
 (1)
(1)
The x-direction momentum analysis of this control volume balances forces from hydrostatic pressure (due to fluid depth) with the inlet and outlet momentum flow rates (Eqn. 2). The pressure forces act inward on the two sides of the control volume, and are equal to the specific gravity of the liquid (liquid density times gravitational acceleration: ρg), multiplied by the average liquid depth on each side (H1/2, H2/2), multiplied the height over which the pressure acts on each side (H1, H2). This results in the quadratic expression on the left side of Eqn. 2. The momentum flow rates through each side (Eqn. 2, right side) are equal to the mass flow rates of liquid through the control volume (in:  , out:
, out:  ) multiplied by the fluid velocities (V1, V2).
) multiplied by the fluid velocities (V1, V2).
 (2)
(2)
Eqn. 1 can be substituted into Eqn. 2 to eliminate V2. The Froude number ( ) can also be substituted in, which represents the relative strength of inflow fluid momentum to hydrostatic forces. The resulting expression can be stated as:
) can also be substituted in, which represents the relative strength of inflow fluid momentum to hydrostatic forces. The resulting expression can be stated as:
 (3)
(3)
This cubic equation has three solutions. One is H1 = H2, which gives the normal open-channel behavior (inlet depth = outlet depth). A second solution gives a negative liquid level, which is unphysical, and can be eliminated. The remaining solution allows for an increase in depth (hydraulic jump) or a decrease in depth (hydraulic depression), depending on the inlet Froude number. If the inlet Froude number (Fr1) is greater than one, the flow is called supercritical (unstable) and has high mechanical energy (kinetic + gravitational potential energy). In this case, a hydraulic jump can form spontaneously or due to some disturbance to the flow. The hydraulic jump dissipates mechanical energy into heat, significantly reducing the kinetic energy and slightly increasing the potential energy of the flow. The resulting outlet height is given by Eqn. 4 (a solution to Eqn. 3). A hydraulic depression cannot occur if Fr1 > 1 because it would increase mechanical energy of the flow, violating the second law of thermodynamics.
 (4)
(4)
The strength of hydraulic jumps increases with inlet Froude numbers. As Fr1 increases, the magnitude of H2/H1 increases and a greater portion of inlet kinetic energy is dissipated as heat [1].

Figure 2: Control volume of a section of an open-channel flow containing a hydraulic jump. Inlet and out mass and momentum flow rates per unit width are indicated. Hydrostatic forces per unit width indicated in lower diagram.
Procedure
NOTE: This experiment uses a relatively powerful submersible pump. The pump should only be plugged into a GFCI outlet to minimize electrical risks. Ensure that no other A/C powered devices are operating near the experiment.
1. Fabrication of open-channel flow facility and tank (see diagram and photograph, Fig. 3)
- Cut lengths of ~6.0 mm thick × 9.5 cm wide clear acrylic sheet with the following lengths: 2×15 cm, 2×25 cm, 1×34 cm, 1×41 cm (Fig. 3a). It is recommended to use a table saw or laser cutter to ensure that the edges are relatively flat and the sheets have equal thickness.
- Cut holes in the lower right corners of the two 60 × 45 cm acrylic sheets to mount the flow meter (Fig. 3a). Cut a hole on the upper right side of the front sheet to install the flow control valve.
- Use acrylic cement (e.g., SCIGRIP 16) to bond the acrylic panels as indicated in Fig. 3a. Ensure adequate ventilation and wear gloves when handling the acrylic cement. It is helpful to apply cement with a needle syringe and use masking tape to position panels during curing. Allow the cement to cure for 24 - 48 hours.
- Install the flow meter on the front panel and affix with the provided screws. Install 1 NPT to ½ NPT reducing fittings on the flow meter inlet and outlet ports. Install ½ NPT to 0.5 in. inner diameter barbed fitting adapters to those fittings.
- Install a 0.5 in. ID and a 0.75 in. ID barbed fitting onto the gate valve (flow rate control). Connect the barbed fitting to the submersible pump with a ~20 cm length of tubing so that the valve handle lines up with the hole on the top right of the acrylic enclosure (Fig. 3b-c).
- Insert the pump into the lower reservoir, and install the valve so that the valve stem passes through the mounting hole and the handle is outside the enclosure (Fig. 3c).
- Insert a vertical acrylic panel near the inlet portion of the flow facility so that there is approximately a 5.0 mm opening below it (Fig. 3b-c). This component will act as the sluice gate, and can be raised and lowered to control flow from the upper reservoir to the channel.
- Fill the upper reservoir loosely with a stainless steel wool scouring pad. This helps distribute inlet water flow evenly across the channel.
- Connect the valve outlet to the flow meter inlet with a length of soft plastic tubing. Connect the flow meter outlet to the upper reservoir with plastic tubing. Ensure that the tubing inlet to the upper reservoir is well anchored so that it does not swing out when the pump is turned on.
- Fill the lower reservoir with water.
2. Performing experiment
- Measure the gap height underneath the gate using a ruler, and denote the value as H1.
- Turn on the pump, and adjust the flow rate using the valve to various flow rates (5 - 15 l min-1). Use a ruler to measure the liquid depth downstream from the gate (H2) for each case.
- Qualitatively observe the shapes of the hydraulic jumps that form at different flow rates. Watch for the minimum threshold flow rate for formation of a hydraulic jump. Sharper, greater amplitude (H2 -H1), jumps should occur at higher flow rates.
3. Data Analysis
- For each flow rate case, calculate the inlet velocity, V1, from the volumetric flow rate.
 where
where  is the volume flow rate and W is the channel width.
is the volume flow rate and W is the channel width. - Evaluate the inlet Froude number (
 ) and theoretical downstream liquid depth for each case (Eqn. 4). Compare these values with measured downstream jump depths.
) and theoretical downstream liquid depth for each case (Eqn. 4). Compare these values with measured downstream jump depths.

Figure 3: a. Schematic and dimensions of facility structure. b. Flow diagram of hydraulic jump facility. c. Labeled photograph of experimental facility.
A hydraulic jump is a phenomenon that occurs in fast-moving open flows when the flow becomes unstable. When a jump occurs, the height of the liquid surface increases abruptly resulting in an increased depth and decreased average flow velocity downstream. An important side effect of this phenomenon is that much of the kinetic energy in the upstream flow is dissipated as heat. Although hydraulic jumps often arise naturally, such as in rivers or the flow into a household sink, they are also purposely engineered into large waterworks to minimize erosion, or increase mixing. This video will illustrate the principles behind hydraulic jumps in a straight channel and then demonstrate the phenomenon experimentally using a small-scale open channel flow facility. After analyzing the results, some applications of hydraulic jumps will be discussed.
Consider the flow in a wide, straight section of an open channel where a hydraulic jump occurs and construct a control volume on a sluice around the jump. If the flow velocity is uniform at the inlet and outlet, conservation of mass yields a simple relation between upstream and downstream fluid depths. Depth multiplied by velocity is constant. A second relation can be found by considering conservation of momentum. Mass transported across the input and output carries momentum with it equal to the corresponding mass flux multiplied by the flow velocity. Hydrostatic forces on the surface of the control volume also contribute to the momentum balance and must be included. These forces are equal to the average pressure on the surface multiplied by the area. At this point, it is useful to introduce the Froude number, a dimensionless quantity named after the English engineer and hydrodynamicist, William Froude. The Froude number characterizes the relative strength of fluid momentum to hydrostatic forces. Now, if the momentum relation is rewritten in terms of the Froude number, with the output velocity eliminated by substitution using the mass relation, the result is a cubic equation in terms of the ratio of downstream and upstream depths. This equation can be simplified by factoring out the trivial solution where the upstream and downstream depths are equal. The two remaining solutions are easily found using the quadratic equation, but the negative solution can be eliminated since it is non-physical. The remaining solution corresponds to an increase in depth, a hydraulic jump, or a decrease in depth, a hydraulic depression, based on the value of the upstream Froude number. If the upstream Froude number is greater than one, the flow has a high mechanical energy and is supercritical or unstable. A hydraulic depression cannot form in this regime because it would increase mechanical energy and violate the second law of thermodynamics. On the other hand, a hydraulic jump can form, either spontaneously or due to some disturbance in the flow. An input Froude number of one represents the minimum threshold for the onset of a hydraulic jump. Hydraulic jumps dissipate mechanical energy into heat, and significantly reduce the kinetic energy, while slightly increasing the potential energy of the flow. As the Froude number increases, so does the ratio of downstream to upstream depths and the amount of kinetic energy dissipated as heat. Now that we understand the principles behind hydraulic jumps, let's examine them experimentally.
First, fabricate the open channel flow facility as described in the text. The facility has an upper and lower reservoir connected by an open channel. Water pumped from the lower reservoir is deposited in the upper reservoir with the flow rate controlled and measured by a valve and flow meter in line with the pump. Steel wool in the upper reservoir helps to evenly distribute the water across the width of the section, and the adjustable sluice gate controls the fluid depth as it enters the channel. After flowing through the channel, the fluid is deposited back into the lower reservoir. When the flow facility is assembled, set it up on a bench and remove any nearby electronic devices. Plug the pump into a GFCI outlet to minimize the risk of electrical shock, and then fill the lower reservoir with water. You are now ready to perform the experiment.
Adjust the sluice gate to approximately five millimeters. Measure the final height of the gap underneath the sluice gate using a ruler, and record this distance as the upstream flow depth, H1. When you are finished, turn on the pump and use the valve to maximize the flow rate without exceeding the scale on the flow meter. Use the ruler again to measure the fluid depth after the hydraulic jump. Record the flow rate, along with this second distance which is the downstream flow depth, H2. Before continuing, observe the shape of the hydraulic jump. You should notice larger, more abrupt transitions for higher flow rates, and smaller, more gradual transitions for lower flow rates. Now, repeat your measurements and observations for successively lower flow rates. Try to determine the minimum threshold flow rate for the formation of a hydraulic jump. Once you have found the threshold flow rate, you are ready to analyze the results.
For each volumetric flow rate, you should have a measurement of the downstream fluid depth. The upstream depth is the same for all cases. Complete the following calculations for each measurement and propagate uncertainties along the way. First, determine the inlet flow velocity. Divide the volumetric flow rate by the channel width and upstream depth. Next, evaluate the upstream Froude number using the definition given before, and substituting in the acceleration due to gravity, as well as the upstream height and velocity. Now, use the Froude number and the non-trivial solution for the jump height to calculate the theoretical downstream depth. Compare the theoretical prediction with the measured downstream depth. At supercritical flow rates, the predictions match the measured depths within experimental uncertainty. Look at your results for the threshold flow rate. Within experimental uncertainty, the Froude number is one, as we anticipated from the theoretical analysis. The rate of mechanical energy loss through the hydraulic jump can also be calculated from these data. First, calculate the mechanical energy of the fluid flowing into the jump, which is the sum of kinetic and potential energy flow rates at the inlet. Now, determine the output energy rate in the same way, but with values at the outlet. The rate of mechanical energy dissipation to heat is the difference between the input and output rates. In this experiment, the energy loss rate can reach about 40% of the inlet energy, or higher. These results highlight the effectiveness of momentum analyses and scale model experiments for understanding and predicting the behavior of hydraulic systems. Now let's look at some other ways hydraulic jumps are utilized.
Hydraulic jumps are an important natural phenomenon with many engineering applications. Hydraulic jumps are often engineered into hydraulic systems to dissipate fluid mechanical energy into heat. This reduces the potential for damage by high velocity liquid jetting from spillways. At high channel flow velocities, sediment can be lifted up from streambeds and fluidized. By reducing flow velocities, hydraulic jumps also reduce the potential for erosion and scouring around pilings. In water treatment plants, hydraulic jumps are sometimes used to induce mixing and aerate flow. The mixing performance and gas entrainment from hydraulic jumps can be observed qualitatively in this experiment.
You've just watched JoVE's introduction to hydraulic jumps. You should now understand how to use a control volume approach to predict the flow behavior, and how to measure this behavior using an open channel flow facility. You've also seen some practical uses for engineering hydraulic jumps in real applications. Thanks for watching.
Results
Upstream Froude numbers (Fr1) and measured and theoretical downstream depths are summarized in Table 1. The measured threshold inlet flow rate for formation of a hydraulic jump corresponds to Fr1 = 0.9 ± 0.3, which matches the theoretical value of 1. At supercritical flow rates (Fr1 > 1) predicted downstream depths match theoretical values (Eqn. 4) within experimental uncertainty.
Table 1 - Measured upstream Froude numbers (Fr1) and downstream liquid depths for H1 = 5 ± 1 mm
| Liquid Flow Rate
( |
Upstream Froude Number (Fr1) | Measured Downstream Depth (H2) | Predicted Downstream Depth (H2) | Notes |
| 6.0 ± 0.5 | 0.9 ± 0.3 | 5 ± 1 | 5 ± 1 | Threshold Froude number for hydraulic jump |
| 11.0 ± 0.5 | 1.7 ± 0.5 | 11 ± 1 | 10 ± 2 | |
| 12.0 ± 0.5 | 1.9 ± 0.6 | 12 ± 1 | 11 ± 2 | |
| 13.5 ± 0.5 | 2.1 ± 0.6 | 14 ± 1 | 13 ± 2 |
Photographs of the hydraulic jumps from the above cases are presented in Fig. 4. No jump is observed for  = 6.0 l min-1 (Fr1 = 0.9). Jumps are observed for the two other cases with Fr1 > 1. A stronger, higher amplitude, jump is observed at the higher flow rate supercritical case.
= 6.0 l min-1 (Fr1 = 0.9). Jumps are observed for the two other cases with Fr1 > 1. A stronger, higher amplitude, jump is observed at the higher flow rate supercritical case.

Figure 4: Photograph of hydraulic jumps, showing critical condition (no jump, Fr1 = 0.9) and jumps at Fr1 = 1.9, 2.1.
Applications and Summary
This experiment demonstrated the phenomena of hydraulic jumps that form at supercritical conditions (Fr > 1) in open channel flows. An experimental facility was constructed to observe hydraulic jump phenomena at varying flow rates. Downstream liquid depths were measured and matched with theoretical predictions.
In this experiment, the maximum reported inlet Froude number was 2.1. The pump was rated to deliver significantly higher flow rates, but resistance in the flow meter limited measurable flow rates to ~14 l min-1. In future experiments, a pump with a greater head rating or a lower pressure drop flow meter may enable a broader range of studied conditions.
Hydraulic jumps are often engineered into hydraulic systems to dissipate fluid mechanical energy into heat. This reduces the potential for damage by high velocity liquid jetting from spillways. At high channel flow velocities, sediment can be lifted up from streambeds and fluidized. By reducing flow velocities, hydraulic jumps also reduce the potential for erosion and scouring around pilings. In water treatment plants, hydraulic jumps are sometimes used to induce mixing and aerate flow. The mixing performance and gas entrainment from hydraulic jumps can be observed qualitatively in this experiment.
For all of these applications, momentum analyses across hydraulic jumps, as discussed here, are key tools for predicting hydraulic system behavior. Similarly, scale model experiments such as those demonstrated in this project, can guide the design of open-channel flow geometries and hydraulic equipment for large-scale engineering applications.
References
- Cimbala, Y.A. Cengel, Fluid Mechanics Fundamentals and Applications, 3rd edition, McGraw-Hill, New York, NY, 2014.





 where
where