5.8: Velocidades Moleculares e Energia Cinética
A teoria cinética molecular explica qualitativamente os comportamentos descritos pelas várias leis de gases. Os postulados desta teoria podem ser aplicados de forma mais quantitativa para derivar essas leis individuais.
Colectivamente, as moléculas de uma amostra de gás têm energia cinética média e velocidade média; mas individualmente, movem-se a velocidades diferentes. As moléculas sofrem frequentemente colisões elásticas nas quais o momentum é conservado. Uma vez que as moléculas que colidem são desviadas a diferentes velocidades, as moléculas individuais têm velocidades muito variáveis. No entanto, devido ao grande número de moléculas e colisões envolvidas, a distribuição da velocidade molecular e a velocidade média são constantes. Esta distribuição de velocidade molecular é conhecida como uma distribuição de Maxwell-Boltzmann, e descreve os números relativos de moléculas em uma amostra geral de gás que possui uma determinada velocidade.
A energia cinética (KE) de uma partícula de massa (m) e velocidade (u) é dada por:
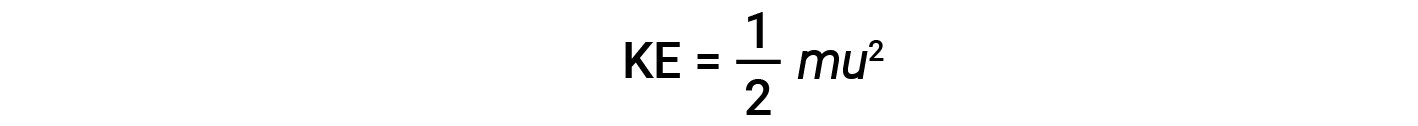
A expressão da massa em quilogramas e da velocidade em metros por segundo produz valores de energia em unidades de joules (J = kg·m2/s2). Para lidar com um grande número de moléculas de gás, usam-se médias tanto para a velocidade como para a energia cinética. Na KMT, a raiz do valor quadrático médio da velocidade de uma partícula, urms, é definida como a raiz quadrada da média dos quadrados das velocidades com n = o número de partículas:
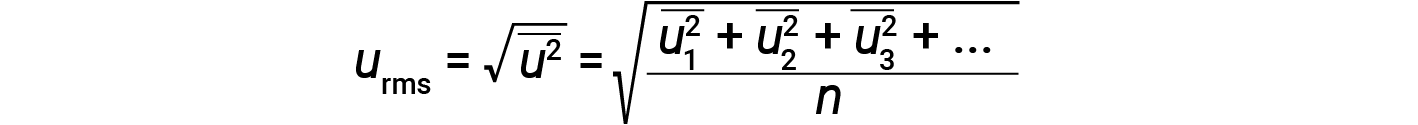
A energia cinética média para um mole de partículas, KEavg, é então igual a:
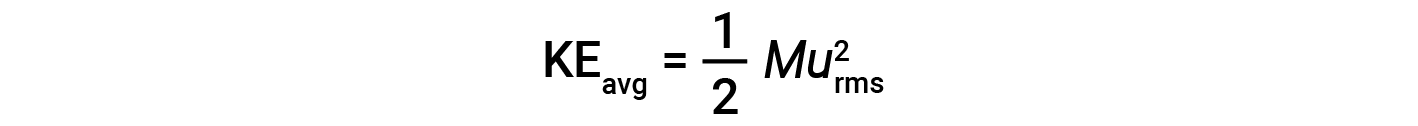
onde M é a massa molar expressa em unidades de kg/mol. A KEavg de um mole de moléculas de gás também é diretamente proporcional à temperatura do gás e pode ser descrita pela equação:
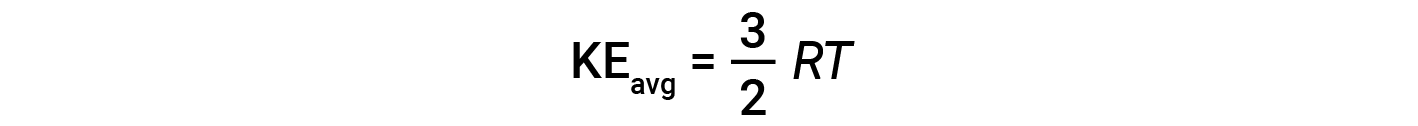
onde R é a constante de gás e T é a temperatura em kelvin. Quando utilizada nesta equação, a forma apropriada da constante de gás é 8,314 J/mol⋅K (8,314 kg·m2/s2·mol·K). Estas duas equações separadas para a KEavg podem ser combinadas e reorganizadas para estabelecer uma relação entre a velocidade molecular e a temperatura:
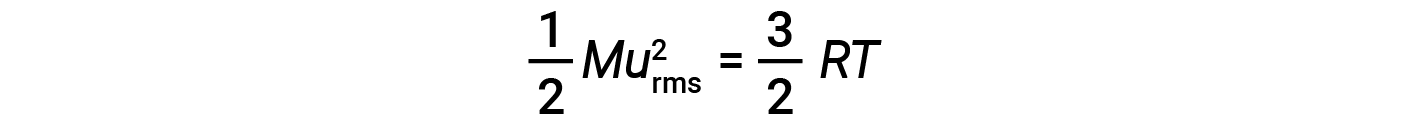
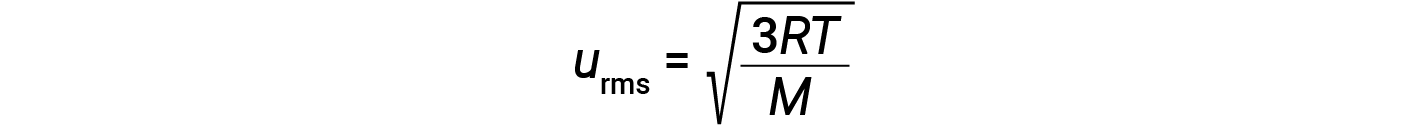
Se a temperatura de um gás aumentar, a sua KEavg aumenta, mais moléculas têm velocidades mais elevadas e menos moléculas têm velocidades mais baixas, e a distribuição muda para velocidades mais elevadas em geral, ou seja, para a direita. Se a temperatura diminuir, a KEavg diminui, mais moléculas têm velocidades mais baixas e menos moléculas têm velocidades mais elevadas, e a distribuição muda para velocidades mais baixas em geral, ou seja, para a esquerda.
A uma determinada temperatura, todos os gases têm a mesma KEavg para as suas moléculas. A velocidade molecular de um gás está diretamente relacionada com a massa molecular. Os gases compostos por moléculas mais leves têm partículas de alta velocidade e urms mais elevados, com uma distribuição de velocidade que atinge velocidades relativamente mais elevadas. Os gases compostos por moléculas mais pesadas têm partículas de velocidade mais baixa, urms mais baixos, e uma distribuição de velocidade que atinge velocidades relativamente mais baixas.
Este texto é adaptado de Openstax, Chemistry 2e, Section 9.5: Kinetic-Molecular Theory.


