Overview
Source: Laboratory of Dr. Andreas Züttel - Swiss Federal Laboratories for Materials Science and Technology
The ideal gas law describes the behavior of most common gases at near-ambient conditions and the tendency of all chemical matter in the dilute limit. It is a fundamental relationship between three measurable macroscopic system variables (pressure, temperature, and volume) and the number of molecules of gas in the system, and is therefore an essential link between the microscopic and the macroscopic universes.
The history of the ideal gas law dates to the middle of the 17th century when the relationship between the pressure and volume of air was found to be inversely proportional, an expression confirmed by Robert Boyle and which we now refer to as Boyle’s law (Equation 1).
P 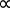 V-1 (Equation 1)
V-1 (Equation 1)
Unpublished work by Jacques Charles in the 1780s, which was extended to numerous gases and vapors by Joseph Louis Gay-Lussac and reported in 1802, established the directly proportional relationship between the absolute temperature and volume of a gas. This relationship is called Charles's law (Equation 2).
V 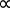 T (Equation 2)
T (Equation 2)
Guillaume Amontons is typically credited with first discovering the relationship between the temperature and pressure of air within a fixed volume at the turn of the 18th century. This law was also extended to numerous other gases by Joseph Louis Gay-Lussac at the beginning of the 19th century and is therefore either referred to as either Amontons’s law or Gay-Lussac's law, stated as shown in Equation 3.
P 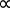 T (Equation 3)
T (Equation 3)
Together, these three relationships can be combined to give the relationship in Equation 4.
V 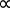 T (Equation 4)
T (Equation 4)
Finally, in 1811, it was proposed by Amedeo Avogadro that any two gases, held in the same volume and at the same temperature and pressure, contain the same number of molecules. This led to the conclusion that all gases may be described by a common constant, the ideal gas constant R, that is independent of the nature of the gas. This is known as the ideal gas law (Equation 5).1,2
PV 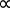 T (Equation 5)
T (Equation 5)
Principles
The ideal gas law, and therefore its characteristic constant R, can also be eloquently derived from first-principles theory in numerous ways, where the important simplifying assumptions are that the molecules have no inherent volume and do not interact. These assumptions are valid in the dilute matter limit, where the volume of empty space occupied by each molecule (e.g. ~10-23 L at ambient conditions) is much larger than the molecule itself (~10-26 L), and where interactions are improbable. It can therefore easily be demonstrated in a number of ways using common laboratory equipment at room temperature, and can be accurately measured using a variety of gases at pressures up to even 10 bar (Figure 1). However, the ideal gas law cannot accurately account for the properties of denser gases at near-ambient conditions (e.g., propane) or for condensation, phenomena that arise as a result of intermolecular interactions. For this reason, numerous more detailed equations of state have succeeded the ideal gas law in the years since its discovery, typically reducing to the ideal gas law in the dilute matter limit.1,2

Figure 1. Comparison of the ideal gas law density to various other common gases at 25 °C and between 0-100 bar.
In this tutorial, we will carefully measure the density of hydrogen gas at increased pressures and temperatures within a fixed volume by weighing a suspended solid sample of known volume: a precisely machined aluminum block. The change in weight of the sample is directly related to the change in fluid density, in which it is floating, by Archimedes’s principle. We will also demonstrate the shortcomings of using a less ideal gas (such as carbon dioxide) at high pressures. Finally, we will visually demonstrate and qualitatively confirm the ideal gas law by performing a simple benchtop experiment where the change in volume of the system due to hydrogen release by a hydrogen storage material is measured. Using any one of these experiments, we can determine the universal constant that describes the relationship between pressure, temperature, and volume for a given amount of gas – the ideal gas constant, R.
Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. Measuring the Volume of the Sample
- Clean the sample carefully and dry it.
- Fill a high-resolution graduated cylinder with enough distilled water to cover the sample. Note the initial volume
- Drop the sample into the water and note the volume change. This is the volume of the sample, V.
- Remove the sample and dry it. Note: alternatively, measured the side length(s) of the sample and calculate its volume using geometry.
2. Load the Sample in the Balance
- Hang the sample in the magnetic suspension balance.
- Install the pressure/temperature chamber around the sample.
- Evacuate the sample environment and refill with hydrogen gas, to 1 bar.
- Measure the sample weight at 1 bar and room temperature, w00.
3. Measure Sample Weight as a Function of Pressure at Room Temperature
- Increase or decrease the pressure in the sample environment to Pi0.
- Allow the sample environment to equilibrate.
- Measure the weight of the sample, wi0.
- Repeat 3.1-3.3 numerous times.
4. Measure Sample Weight as a Function of Pressure at Various Temperatures
- Set the temperature to Tj and allow it to equilibrate.
- Set the pressure of hydrogen gas to 1 bar.
- Measure the sample weight at 1 bar and Tj, w0j.
- Increase or decrease the pressure to Pij and allow it to equilibrate.
- Measure the weight of the sample, wij.
- Repeat 4.4-4.5 numerous times.
- Repeat 4.1-4.6 as desired.
5. Calculate the Ideal Gas Constant
- Tabulate the measured values {Tj, Pij, and wij} where P0j is always 1 bar and T0 is the measured room temperature.
- Calculate and tabulate the differences Δwij and ΔPij at each temperature Tj using Equation 6 and Equation 7.
Δwij = wij - w0j (Equation 6)
Δwij = Pij - P0j = Pij - 1 bar (Equation 7) - Calculate Rij for each measurement, and average over all values to determine the ideal gas constant, R. Alternatively, plot the product of ΔPij and V as a function of the product of Δwij (divided by the molecular weight, MW) and Tj, and perform a linear regression analysis to determine the slope, R. (Equations 8 and 9) For hydrogen, MW = 2.016 g/mol.
ΔP V = Δn RT (Equation 8)
 (Equation 9)
(Equation 9)
The ideal gas law is a fundamental and useful relationship in science as it describes the behavior of most common gases at near-ambient conditions.
The ideal gas law, PV=nRT, defines the relationship between the number of molecules of gas in a closed system and three measurable system variables: pressure, temperature, and volume.
The ideal gas law relies on several assumptions. First, that the volume of the gas molecules is negligibly small. Second, that the molecules behave as rigid spheres that obey Newton's laws of motion. And finally, that there are no intermolecular attractive forces between the molecules. They only interact with each other through elastic collisions, so there is no net loss in kinetic energy. Gases deviate from this ideal behavior at high pressures, where the gas density increases, and the real volume of the gas molecules becomes important. Similarly, gases deviate at extremely low temperatures, where attractive intermolecular interactions become important. Heavier gases may deviate even at ambient temperature and pressure due to their higher density and stronger intermolecular interactions.
This video will experimentally confirm the ideal gas law by measuring the change in density of a gas as a function of temperature and pressure.
The ideal gas law is derived from four important relationships. First, Boyle's law describes the inversely proportional relationship between the pressure and volume of a gas. Next, Gay-Lussac's law states that temperature and pressure are proportional. Similarly, Charles's law is a statement of the proportionality between temperature and volume. These three relationships form the combined gas law, which enables the comparison of a single gas across many different conditions.
Finally, Avogadro determined that any two gases, held at the same volume, temperature and pressure, contain the same number of molecules. Because gases under the same condition typically behave the same, a constant of proportionality, called the universal gas constant (R), could be found to relate these parameters, enabling the comparison of different gases. R has units of energy per temperature per molecule; for example, joules per kelvin per mole.
The ideal gas law is a valuable tool in understanding state relationships in gaseous systems. For example, in a system of constant temperature and pressure, the addition of more gas molecules results in increased volume.
Similarly, at constant temperature in a closed system, where no molecules are added or subtracted, the pressure of a gas is increased when volume is decreased.
A magnetic suspension balance can be used to confirm the ideal gas law experimentally by measuring the physical properties of a system. The weight of a solid sample of constant mass and volume can serve as a probe of the properties of the gas around it.
As pressure increases in the system, at constant system volume and temperature, the amount of gas molecules in the system increases, thereby increasing the gas density. The rigid solid sample submerged in this gas is subject to buoyancy, and its apparent weight decreases although its mass is unchanged. The change in gas density can be determined because of Archimedes principle, which states that the change in object weight is equal to the change in weight of the gas that is displaced.
The precise behaviors of the gas density under different pressure and temperature conditions will correspond to the ideal gas law if the previously described approximations hold true, enabling the straightforward calculation of the universal gas constant, R.
In the following series of experiments, a microbalance will be used to confirm the ideal gas law and determine the universal gas constant, R, by measuring the density of hydrogen as a function of temperature and pressure. First, carefully clean the sample, in this case a finely machined aluminum block, with acetone, and dry. Measure the volume of the sample by filling a graduated cylinder with enough distilled water to cover the sample. Note the initial volume. Immerse the sample in the water, and note the volume change.
Remove and carefully clean and dry the sample. Next, load it into the magnetic suspension balance, in this case located inside of a glove box. Install the pressure-temperature chamber around the sample. The sample is now magnetically suspended in a closed system, not touching any of the walls.
Evacuate the sample environment and refill with hydrogen gas, to a pressure of 1 bar.
Measure the sample weight, and label it as the initial weight at room temperature. Next, increase the pressure in the sample environment to 2 bar, and allow it to equilibrate. Measure the weight at the new pressure. Repeat these steps several times at a number of pressures, to acquire a series of sample weights at corresponding pressures, all at room temperature.
Next, measure weight as a function of pressure at a higher temperature. First evacuate the sample environment, then increase the temperature to 150 °C and allow it to equilibrate. Then, increase the pressure to 1 bar. Measure the sample weight, and label it as the initial weight at 150 °C and 1 bar. Increase the pressure, allow it to equilibrate, and measure the weight. Repeat these steps in order to measure a series of sample weights at a range of pressures. To obtain more data, repeat the series of weight measurements at other constant temperatures and pressures.
To calculate the ideal gas constant, tabulate the measured values of sample weight at each temperature and pressure.
Next, calculate the differences between all pairs of sample weights within a single temperature set to obtain all possible combinations of the change in weight as a function of change in pressure, or Δw. This change is equivalent to the change in weight of the hydrogen gas that is displaced by the sample.
Similarly, calculate all corresponding differences in pressure to obtain change in pressure, or ΔP. Tabulate all pairs of changes in weight and pressure for each temperature. Convert the units of temperature to kelvin and the units of pressure to pascals.
Since the volume and temperature remain constant for each series of measurements, the ideal gas law can be written as ΔPV=ΔnRT. Since Δn is equal to Δw divided by the molecular weight of hydrogen, calculate each value of Δn for each value of Δw.
Plot the product of pressure change and sample volume, as a function of the product of Δn and temperature. Perform a linear regression analysis to determine the slope, which will equal the universal gas constant if done correctly.
The ideal gas equation is used in many real world scenarios, typically those performed with gases at ambient temperature and pressure. All gases deviate from ideal behavior at high pressure; however, some gases, such as carbon dioxide, deviate more than others. In this experiment, deviations from ideal behavior were measured for carbon dioxide gas. The procedure was identical to the previous experiment conducted with hydrogen.
A plot of pressure times volume versus moles times temperature was plotted, and the ideal gas constant calculated from the slope of the plot. Carbon dioxide deviated significantly from ideal behavior, even at ambient conditions. This behavior was caused by attractive intermolecular interactions, which was not observed with hydrogen.
The ideal gas law is used in the identification and quantification of explosive gases in air samples. This research area is of extreme importance to the military and security.
Here, explosive components of a gas sample were quantified using temperature desorption gas chromatography. The data, as well as the ideal gas law were then used to quantify these dangerous substances.
You've just watched JoVE's Introduction to the ideal gas law. After watching this video, you should understand the concept of the law, and situations where the equation is applicable.
Thanks for watching!
Subscription Required. Please recommend JoVE to your librarian.
Results
The ideal gas law is a valid description of the actual gas properties of numerous common gases at conditions near ambient (Figure 1 inset) and is therefore useful in the context of many applications. The limitations of the ideal gas law in describing systems under conditions of high pressures or low temperatures can be explained by the increasing importance of molecular interactions and/or the finite size of the gas molecules contributing to the system’s properties. Therefore, gases with strong, attractive intermolecular interactions (arising from dipole-dipole interactions, including hydrogen bonding, ion-dipole interactions, or van der Waals interactions) will exhibit higher densities than the ideal gas. All gases will also have a repulsive component at high densities due to the fact that more than one molecule cannot occupy the same location, lending a decrease in density over the ideal gas. Gases like hydrogen and helium show a more significant contribution from the repulsive force due to finite molecular size, and therefore have slightly lower densities at high pressures. Methane and carbon dioxide show much more significant contributions to their properties from attractive interactions, lending them higher densities than the ideal gas until very high pressures, where the repulsive term dominates (at much higher than 100 bar at 25 °C).

Figure 2. Equilibrium adsorption uptake isotherm of CO2 on high surface area, superactivated carbon MSC-30, at 25 °C.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
The ideal gas law is such a fundamental equation of the chemical sciences that it has a plethora of uses both in day-to-day laboratory activities as well as in calculations and modeling of even highly complex systems, at least to first approximation. Its applicability is limited only by the approximations inherent to the law itself; at near-ambient pressures and temperatures, where the ideal gas law is well valid for many common gases, it is widely employed in the interpretation of gas-based systems and processes. Two examples of devices that operate on principles, which can be reconciled by use of the ideal gas law, are the gas thermometer and the Stirling engine.
One specific application is in measuring the quantity of gas adsorption (physisorption) on the surface of a solid material. Adsorption is the physical phenomenon whereby gas molecules leave the gas phase and enter into a densified phase near the surface of a solid (or perhaps a liquid) due to attractive intermolecular interactions (dispersion forces) between the solid and the gas. The role of adsorption can be neglected for many bulk materials (such as glass and stainless) steel at ambient conditions, but becomes very important for porous materials with a large accessible surface area, especially at low temperatures.3 The volumetric Sieverts's method and the gravimetric method of quantifying physical adsorption rely on knowing the equation of state of the gas in the system. At low pressures and ambient temperature, the ideal gas law is valid for many gases, and can be used to accurately determine the adsorbed quantity of gas in a similar way as described in the protocol for determining R above. For example, in gravimetric measurements of the buoyancy of a high-surface-area sorbent under conditions where the ideal gas law is in fact valid, the difference between the Δwactual measured and the Δwideal calculated using the ideal equation of state can be attributed to the change in weight of the adsorbed phase. (Equation 10) Equilibrium gas adsorption isotherms can thus be measured by tabulating this deviation, Δwads, as a function of pressure at a fixed temperature (see Figure 2), a standard procedure in the characterization of porous materials.
Δwads = Δwactual - Δwideal (Equation 10)
Subscription Required. Please recommend JoVE to your librarian.
References
- Zumdahl, S.S., Chemical Principles. Houghton Mifflin, New York, NY. (2002).
- Kotz, J., Treichel, P., Townsend, J. Chemistry and Chemical Reactivity. 8th ed. Brooks/Cole, Belmont, CA (2012).
- Rouquerol, F., Rouquerol, J., Sing, K.S.W., Llewellyn, P., Maurin, G. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications.Academic Press, San Diego, CA. (2014).





 (Equation 9)
(Equation 9)