ERRATUM NOTICE
Important: There has been an erratum issued for this article. Read more …
Summary
A setup for X-ray beam induced current measurements at synchrotron beamlines is described. It unveils the nanoscale performance of solar cells and extends the suite of techniques for multi-modal X-ray microscopy. From wiring to signal-to-noise optimization, it is shown how to perform state-of-the-art XBIC measurements at a hard X-ray microprobe.
Abstract
X-ray beam induced current (XBIC) measurements allow mapping of the nanoscale performance of electronic devices such as solar cells. Ideally, XBIC is employed simultaneously with other techniques within a multi-modal X-ray microscopy approach. An example is given herein combining XBIC with X-ray fluorescence to enable point-by-point correlations of the electrical performance with chemical composition. For the highest signal-to-noise ratio in XBIC measurements, lock-in amplification plays a crucial role. By this approach, the X-ray beam is modulated by an optical chopper upstream of the sample. The modulated X-ray beam induced electrical signal is amplified and demodulated to the chopper frequency using a lock-in amplifier. By optimizing low-pass filter settings, modulation frequency, and amplification amplitudes, noise can efficiently be suppressed for the extraction of a clear XBIC signal. A similar setup can be used to measure the X-ray beam induced voltage (XBIV). Beyond standard XBIC/XBIV measurements, XBIC can be measured with bias light or bias voltage applied such that outdoor working conditions of solar cells can be reproduced during in-situ and operando measurements. Ultimately, the multi-modal and multi-dimensional evaluation of electronic devices at the nanoscale enables new insights into the complex dependencies between composition, structure, and performance, which is an important step towards solving the materials' paradigm.
Introduction
In a world where the demand for electrical energy is constantly rising, a clean and sustainable energy source is increasingly necessary. One possibility to tackle these demands are photovoltaic (PV) systems1,2,3. For a directed and efficient way of developing next-generation solar cells, it is necessary to understand how the composition and structure of the solar cells affect their performance4. Typical questions in solar cell development include: Which types of defects are most detrimental, and where are they located5,6? Are there inhomogeneities in the elemental distribution, and what is their impact7,8,9? How do the solar cells change upon module assembly and aging10,11?
As a solar cell is only as good as its weakest part, it is especially important to understand the effect of compositional and structural variation on the performance in polycrystalline solar cells that suffer inherently from inhomogeneities7,8. This is particularly true for thin film (TF) solar cells, which contain absorber layers with crystallite sizes in the micrometer range. Here, the effect of grain boundaries on performance is of highest interest, but their small size and the fact that they are buried in an entire layer stack pose unique characterization challenges. Furthermore, the complex chemistry of multi-component absorber layers with co-existing phases and internal gradients require sophisticated characterization methods12.
Synchrotron-based hard X-ray microscopes are able to meet the characterization challenges of TF solar cells: they provide X-ray spot sizes down to the nanometer scale13,14,15,16 and the penetration depth of hard X-rays allows to probe the different device layers17, including buried absorber layers. With a wealth of different measurement techniques at a scanning X-ray microscope, it becomes possible to simultaneously study not just one, but many different aspects of solar cells within multi-modal measurements and to correlate the observed characteristics. For example, X-ray beam induced current (XBIC) measurements have successfully been combined with X-ray fluorescence (XRF)7,18,19, X-ray excited optical luminescence (XEOL)20,21, and X-ray diffraction (XRD)22 to correlate the electrical performance with composition, optical performance, and structure, respectively23.
During XBIC measurements of solar cells or other devices under test (DUT)24,25, the incident X-ray photons set off particle showers consisting of electrons and photons, resulting in a multitude of excited electron-hole pairs per incident X-ray photon in the semiconducting absorber material. Finally, the electron-hole pairs thermalize to the band edges of the solar cell absorber. Therefore, these X-ray excited charge carriers can be treated like charge carriers that are generated by the absorption of photons with energies just above the bandgap during normal solar cell operation, and the resulting current or voltage can be measured as X-ray beam induced current23,26,27 or voltage (XBIV)28,29 similar to more common measurements like electron-beam induced current (EBIC) or laser-beam induced current (LBIC). Consequently, the XBIC/XBIV signal not only depends on the thickness of the absorber layer, but also on the electric performance of the DUT, both at the microscopic and macroscopic level, including the local bandgap, Fermi-level splitting, and recombination. Thus, we are able to map local variations of the charge-carrier collection efficiency that is defined as the probability that an externally excited electron-hole pair in the absorber layer is collected at the electrical contacts of the DUT.
Note that only electron-hole pairs that are generated in the absorber layer of the DUT contribute to the XBIC/XBIV signal. Charge carriers generated in other layers such as the metallic contacts or substrate will immediately recombine, as they have no possibility of being separated by the junction. Therefore, other layers only affect XBIC/XBIV measurements via secondary effects such as parasitic X-ray absorption or the emission of secondary photons and electrons that may be re-absorbed in the absorber layer. In contrast, all layers potentially contribute to the XRF signal.
Given that the XBIC and XBIV signals can be small (often, variations in the sub-picoampere and nanovolt range are of interest), the signals are easily buried in noise. Therefore, we suggested to utilize lock-in amplification to extract the XBIC and XBIV signals30. For this purpose, the incoming X-ray beam is modulated by an optical chopper as indicated in Figure 1. This modulation carries over to the signal produced by the DUT. Before the signal is fed into the lock-in amplifier (LIA), a pre-amplifier (PA) is typically used to match the raw signal intensity with the range of the analog-to-digital converter at the input of the digital LIA. The LIA mixes the modulated measurement signal with the reference signal. By employing a low-pass filter, only frequencies close to the reference signal are passed through and amplified31. This allows for an effective extraction of the XBIC or XBIV signal from a noisy background.
In the protocol, we introduce the prerequisites and motions necessary for taking successful XBIC measurements including the raw signal (direct current, DC) and the modulated signal (alternating current, AC). Beyond describing technical details, we discuss an XBIC setup in the context of multi-modal measurements at beamline P06 at PETRA III13. Please note that, compared to most laboratory experiments, the environment of hutches at hard X-ray nanoprobes requires particular planning and consideration. Specifically, multi-modal measurements with nanometer-scale resolution challenge the experimentalists with a variety of specific constraints. For example, electronic noise is often present with great amplitudes from piezo-driven motors and other equipment, such as the power supplies of detectors. Furthermore, a multitude of devices and detectors needs to be arranged at optimized geometry without interfering with each other nor inducing vibrations. Figure 1 depicts a typical setup for XBIC measurements in combination with XRF and small/wide angle X-ray scattering (SAXS/WAXS) measurements.
Protocol
1. Setting up the measurement environment
- Requirements for lock-in amplified XBIC measurements
- Make sure to have the following available: a nano- or micro- focusing X-ray beamline; an X-ray chopper that absorbs periodically the majority of the X-rays; a PA; a LIA; modules for remote control of the chopper, PA, and LIA; a data acquisition (DAQ) system; a DUT.
- Sample holder fabrication
- Use a kinematic base for the sample holder. This makes it possible to re-position samples to within micrometer precision and saves valuable beamtime. Furthermore, it allows for the positioning of samples across different measurement platforms with different mounting systems.
- Design the sample holder in a way that it provides maximum freedom to place different detectors in proximity around the sample, while also being compatible with X-ray transparent samples and measurement techniques such as SAXS or WAXS. Typically, this translates into minimal sample holder size, stiffness down to the nanometer scale and being lightweight.
- Design a printed circuit board (PCB) to be used as a mount for the electronic device for XBIC measurements. Although a dedicated PCB with direct connection to a coaxial cable is not necessary strictly speaking, it can play a substantial role in the reduction of noise in comparison to loose wiring, where the wires act as antennae.
NOTE: Ideally, a Faraday cage would shield the sample from electromagnetic fields. However, this is in most cases not compatible with measurement geometries.
- Sample contacting
- Glue the electronic DUT onto the PCB. Depending on the materials and requirements for later removal of the DUT, it is recommended to use nail polish, instant glue, composite glue, or silicon glue.
- Ensure that no mounting part or wiring blocks the incident X-ray beam nor obstructs the line of sight of any other detectors employed such as for XRF measurements.
- Contact both terminals of the DUT.
NOTE: There are various ways to contact electronic devices, and the best choice depends on specific sample properties, where adhesion, chemical or mechanical resistance, and available space are arguments for one or another contacting method. - Connect the front contact (the upstream contact facing the incident X-ray beam) with the shield of the coaxial cable.
- Connect the back contact (the downstream contact) with the core of the coaxial cable.
- Ground the front contact (shield of the coaxial cable).
NOTE: The incoming beam leads to the ejection of electrons from the DUT, which leads to a compensation current in the measurement circuit that is easily misinterpreted as XBIC. Therefore, the front contact should always be grounded23. It may be necessary to test different grounding methods to minimize the potential variations. - Consider Figure 2 as an example of a sample holder consisting of a kinematic base, an aluminum holder, and a PCB with a solar cell connected to one of the two coaxial connectors.
- Arrangement of sample and detectors
- Mount the sample on the holder.
- Mount the sample holder on the sample stage.
- Place the center of rotation of the stage into the focus of the X-ray beam.
- Place the sample into the center of rotation of the rotation stage.
- Rotate the stage such that the plane of interest is perpendicular to the incident beam to minimize the beam footprint and maximize the spatial resolution.
- In case of multi-modal measurements, place the detector(s) around the sample.
NOTE: Depending on the X-ray optics, there is little room to place detectors upstream of the sample. For non-X-ray-transparent samples, the fluorescence detector should be looking at the X-ray focus point under an angle of 10-20° to the sample plane such that self-absorption for the elements of interest and counts from scattering are minimized.
- Chopper installation
- Mount a motorized stage, with the ability to move perpendicularly to the X-ray beam, upstream of the sample.
NOTE: While this motorized stage is not necessary, it allows for moving the chopper in and out of the X-ray beam without entering the hutch, thus enabling higher throughput and greater stability. - Install an optical chopper onto the motorized stage to modulate the incoming signal.
NOTE: Ideally, the chopper is placed far upstream of the sample such that it does not induce any vibrations on the X-ray optics or the sample by the motor or air turbulence, respectively. Nevertheless, good results with vibration amplitudes below 100 nm have been obtained with the chopper wheel being as close as 10 mm to the sample, while chopping at > 6 kHz.
- Mount a motorized stage, with the ability to move perpendicularly to the X-ray beam, upstream of the sample.
- Reduction of background light
- Turn off sources of light in the hutch whenever possible and shield any others, including any small lights on the LIA and chopper wheel controller. At some beamlines, there is a light that is turned on when the hutch is searched. However, this light should not remain on during the measurement.
2. Setting up XBIC measurements
- See Figure 1 for a schematic representation of necessary hardware components and wiring.
- Setup of a pre-amplifier
- Place a PA in proximity of the sample.
NOTE: Some LIAs come with an integrated PA. In this case, PA settings are applied in a similar manner to the settings for the LIA. - Connect the PA to a control unit outside of the hutch to enable the remote change of amplification settings without entering the hutch. Ideally, the control unit is connected to the beamline control, and the PA settings are automatically recorded.
- Power the PA from a clean power circuit.
NOTE: Devices like vacuum pumps can pollute the power circuit and should therefore be powered separately from high-precision electronics such as PA and LIA that can transfer variations in the power supply to the measurement signal. For this reason, beamlines usually have clean and polluted power circuits. Many amplifiers can even be operated from batteries. - Connect the sample through the BNC connector on the sample mount.
- Ensure that the sample wiring is strain-relieved so that it will not restrict the sample movements.
- Apply a bias voltage via the PA if the XBIC signal shall not be measured under short-circuit conditions. Do not apply any bias voltage if the XBIV signal shall be measured under open-circuit conditions.
- Measure the signal amplitude of the DUT under measurement conditions (i.e., usually in dark) and under working conditions (e.g., with room light and beamline microscope light on) to test the signal range.
- Make sure that the signal amplitude of the DUT matches the input range of the PA, and take precautions to avoid oversaturation under high signal conditions (e.g., turned on room light), as oversaturation can destroy the PA.
- Make sure that the sensitivity of the PA matches its output range and the input range of the LIA. It is good practice to keep the amplification of the PA at the minimum sensitivity whenever no measurement is going on to avoid accidental oversaturation.
- Connect the DUT to the PA. Given the small signal amplitude, it is critical to keep the wiring short.
NOTE: Cables carrying XBIC signal should not be intertwined with other cables as these might induce noise. Sources of noise include scanning stages and detectors as they are used for XRF. Different wire positions may be tested to minimize noise. For further noise reduction, the wire can be wrapped in grounded aluminum foil or triaxial cables can be used. - Split the pre-amplified signal into three parallel signal branches to separately record the DC (positive and negative) and modulated AC components.
Note: Alternative signal paths are mentioned in part (a) of the discussion section. - Connect two signal branches to voltage-to-frequency (V2F) converters, one of which with inverted input signal range to accept the negative DC signal.
- Place a PA in proximity of the sample.
- Electrical setup of a lock-in amplifier
- Connect the LIA to a control unit outside of the hutch to enable the remote change of amplification settings without entering the hutch. Ideally, the control unit is connected to the beamline control, and the LIA settings are automatically recorded.
- Power the LIA from a clean power circuit and keep it at a distance from possibly noisy instruments.
- Make sure that the output of the PA matches the input of the LIA under all conditions, as oversaturation can damage the LIA. It is good practice to keep the LIA input range at its maximum whenever no measurement is going on to avoid accidental oversaturation.
- Feed the modulation frequency from the optical chopper as reference signal into the LIA.
NOTE: The reference frequency can either be provided by an oscillator of the LIA, driving the chopper and thus allowing remotely controlling it, or being input from the chopper controller as a reference to the LIA. A combination of both is also possible. - Connect the third branch of the pre-amplified XBIC signal to the LIA input.
- Output the root-mean-squared (RMS) amplitude of the lock-in amplified
 signal as analog AC signal of the DUT.
signal as analog AC signal of the DUT.
NOTE: As is always positive, a splitting of the signal and inverting of one branch is not necessary so long as the signal input at the V2F converter is not negative. If the phase information shall also be recorded, it is recommended to output the phase
is always positive, a splitting of the signal and inverting of one branch is not necessary so long as the signal input at the V2F converter is not negative. If the phase information shall also be recorded, it is recommended to output the phase  in addition to
in addition to  , or the in-phase component
, or the in-phase component  and quadrature component
and quadrature component  .
. - Connect the output of the LIA to a third V2F channel.
- Connect the V2F converters to the DAQ units and beamline software to store the three XBIC signal components with corresponding time and pixel information.
NOTE: There are alternative methods to V2F converters for XBIC DAQ. For example, the voltage output from PA and LIA can be digitized directly, or digital readout of the amplifiers can be integrated in the beamline control system. However, the presented approach is compatible with most synchrotron beamlines, as V2F converters are generally available.
3. XBIC measurements
- Choosing well-suited XBIC measurement conditions
- Beware of the trade-off of scanning speed, chopper frequency, and low-pass filter settings as discussed later in the manuscript.
- Optimizing XBIC measurement parameters
- Make sure that the DUT is shielded from all lights in the hutch.
- Set all amplifications of PA and LIA to the minimum, and input ranges to the maximum to avoid oversaturation.
- Set the frequency of the chopper, which is the modulation frequency of the signal and the reference frequency for its demodulation.
NOTE: As a rule of thumb, the frequency selected should be as high as possible under the constraints of (a) fast enough response of the DUT, (b) fast enough amplification chain, (c) acceptable level of vibrations induced by the chopper. Furthermore, frequencies that are multiples of common noise frequencies such as 50/60 Hz or 45 kHz should be avoided. - Set the amplification of the PA such that (a) the maximum output amplitude is well within the maximum input range of the LIA and (b) the response of the PA is fast enough for the chosen chopper frequency. For the optimization of the amplifier settings in this tradeoff, we refer to the subsection (b) of the discussion section.
CAUTION: Before allowing more photons onto the DUT (e.g., when entering the hutch), set the amplifiers again to their maximum input range and to their minimum amplification to avoid overloading. Ideally, this is implemented directly in the scan commands. - Set the input range of the LIA to match the signal amplitude after pre-amplification for the region of interest with the strongest signal.
- In the LIA, split and mix the signal from the DUT with the reference signal from the chopper and a 90° phase-shifted reference signal as discussed in subsection (c) of the representative results.
- Set the low-pass filter frequency of the LIA to the minimum that is compatible with the scanning speed.
NOTE: As a rule of thumb, set it to at least an order of magnitude below the chopping frequency, and an order of magnitude above the sampling rate. Ideally, the low-pass filter frequency should be chosen such that common noise frequencies are not passed, most importantly below 50/60 Hz to cut off the grid frequency. For details, we refer to subsection (e) of the representative results. - Set the amplification scale for the analog output of the lock-in amplified signal such that it matches the input range of the V2F and does not exceed it.
- Set soft- or hardware limits for amplifier outputs according to the input range of the following devices to prevent saturation.
- Taking XBIC measurements
NOTE: With proper amplification parameters set for XBIC measurements, and automated control and readout implemented, there is no further action required to take XBIC measurements apart from starting a scan. - Post-processing of XBIC Data
- Go along the signal chain from the DUT to the data acquisition unit, where the signal is saved as count rate
 (Hz), to convert the count rate back to a current.
(Hz), to convert the count rate back to a current.
- Get the amplification factor
 (V/A) at the PA, where the
(V/A) at the PA, where the  signal (measured in ampere) is amplified and converted to a voltage.
signal (measured in ampere) is amplified and converted to a voltage. - Get the amplification factor
 (V/V) at the LIA.
(V/V) at the LIA. - Get the voltage acceptance range
 (V) of the V2F converter that is projected onto the frequency range
(V) of the V2F converter that is projected onto the frequency range  (Hz).
(Hz). - Consider additional waveform factors: the output signal of the LIA is the RMS amplitude, but the signal of interest is the peak-to-peak value of the modulated input signal.
- Get the amplification factor
- Multiply the count rate of each pixel with the conversion term
 in the following equation to get the XBIC values in ampere from the frequency values sorted by the DAQ:
in the following equation to get the XBIC values in ampere from the frequency values sorted by the DAQ:
(1) with
with  ,
,
where is a factor which depends on the waveform of the modulation32.
is a factor which depends on the waveform of the modulation32.
NOTE: For an incoming sine wave,
 ; for a triangle wave,
; for a triangle wave, 
 ; and for a square wave,
; and for a square wave,  . Typical values for the measurement of thin-film solar cells at hard X-ray nanoprobes are:
. Typical values for the measurement of thin-film solar cells at hard X-ray nanoprobes are:  ,
,  ,
,  ,
,  .
. - For the eventual correction of the raw XBIC signal
 for topological variations, use28:
for topological variations, use28:
(2) ,
,
with being the X-ray attenuation coefficient33 and
being the X-ray attenuation coefficient33 and  the mass density for the absorber element
the mass density for the absorber element  which can be measured through simultaneous XRF measurements17.
which can be measured through simultaneous XRF measurements17. - For the eventual conversion of the XBIC signal into charge collection efficiency,
 , use23:
, use23:
(3) ,
,
where and
and  are the generation and collection rate of electron-hole pairs,
are the generation and collection rate of electron-hole pairs,  is the rate of incident photons,
is the rate of incident photons,  is the elementary charge, and
is the elementary charge, and  is a material constant.
is a material constant. - For the eventual calculation of the material constant
 , use:
, use:
(4) ,
,
where is the energy deposited in the absorber layer of the DUT per incident X-ray photon,
is the energy deposited in the absorber layer of the DUT per incident X-ray photon,  is the bandgap of the absorber material, and
is the bandgap of the absorber material, and  is a constant.
is a constant.
NOTE: The factor accounts for the energy efficiency of electron-hole pair generation. It is often approximated23,34 as
accounts for the energy efficiency of electron-hole pair generation. It is often approximated23,34 as  .
. - For the eventual estimation of the injection level,
 , from the XBIC signal, use:
, from the XBIC signal, use:
(5) ,
,
where is interpreted as the number of sun equivalents,
is interpreted as the number of sun equivalents,  is the X-ray beam cross-section, and
is the X-ray beam cross-section, and  is the short-circuit current density under standard measurement conditions35.
is the short-circuit current density under standard measurement conditions35.
- Go along the signal chain from the DUT to the data acquisition unit, where the signal is saved as count rate
Representative Results
The key advantage of using lock-in amplification for XBIC measurements is the dramatic increase of the signal-to-noise ratio as compared to measurements with standard amplification. The measurement settings that are particularly critical for successful lock-in-amplified XBIC measurements will be discussed in the first five sections. They are: (a) signal modulation; (b) pre-amplification; (c) signal mixing in the LIA; (d) low-pass filter frequency of the LIA; (e) low-pass filter roll-off of the LIA.
Illustrations of the impacts of these settings are demonstrated in Figure 3, Figure 4, Figure 6. For the measurements, a laboratory setup used a red laser ( ) in place of an X-ray beam, modulated at
) in place of an X-ray beam, modulated at  2177.7 Hz by an optical chopper. Fluorescent tubes served as a source for bias light. The DUT was a thin-film solar cell with a Cu(In,Ga)Se2 (CIGS) absorber. Although different measurement settings would be chosen for other DUT, the general guidelines described here to find suitable settings are valid for a variety of DUT such as solar cells with different absorber layers or nanowires. The PA was used with an amplification factor of
2177.7 Hz by an optical chopper. Fluorescent tubes served as a source for bias light. The DUT was a thin-film solar cell with a Cu(In,Ga)Se2 (CIGS) absorber. Although different measurement settings would be chosen for other DUT, the general guidelines described here to find suitable settings are valid for a variety of DUT such as solar cells with different absorber layers or nanowires. The PA was used with an amplification factor of  . The effects discussed here apply equally to other pre-amplifiers. If nothing else is specified, the low-pass filter roll-off of the LIA was 48 dB/oct.
. The effects discussed here apply equally to other pre-amplifiers. If nothing else is specified, the low-pass filter roll-off of the LIA was 48 dB/oct.
The following sections (f)-(i) show exemplary results to display the possibilities and challenges of XBIC measurements in conjunction with other measurement modes. In (f), specific challenges of XBIC measurements in fly-scanning mode are discussed. In (g), XBIC and XRF measurements of a CIGS solar cell are combined, and the effect of lock-in amplification is discussed with bias voltage applied. In (h), XBIV is added as a measurement mode for a CIGS solar cell. In (i), XBIC and compositional data from XRF of a CdS nanowire are shown. For all XBIC measurements in sections (f) to (i), we used a PA and a LIA as specified in the Table of Materials and Reagents.
(a) Modulation of the Incoming Signal
Figure 3 shows the pre-amplified DUT response measured by a scope without (top row) and with (bottom row) bias light turned on. As the PA converts currents to voltages, the displayed signal is in volts. It is negative due to the contacting of the solar cell, with the p- and n-type contacts connected to the shield and core of the input of the PA, respectively. In XBIC measurements, the solar cell contacting is governed by the necessary grounding of the front contact as discussed in section 1.3.6. of the protocol.
Comparing Figure 3A and Figure 3D, we note an offset signal on the order of 8 mV that is shifted to -65 mV by turning on the bias light from fluorescence tubes. Furthermore, the signal variation on short timescales is significantly enhanced by the bias light. Such a bias offset of roughly 70 mV can prove problematic, due to limits in the acceptance range of the PA and LIA. As we would like to use the full range of the PA, a small offset as in Figure 3A-C is preferable. Therefore, all sources of unintentional bias, such as ambient lighting, should be eliminated.
Adding a chopped photon source, as displayed in Figure 3B,C,E,F, increases the induced signal by the same amount - roughly 66 mV - for both with and without bias light, when the beam passes through the chopper blade; when the beam is blocked by the blade, the signal remains at the level of the respective offset, as is expected. The frequency of the chopper is distinct in the signal of Figure 3B and 3E with a period of  ms.
ms.
In Figure 3D-F, we note an additional modulation at a frequency of 90 kHz. The source of this high-frequency modulation is the electronic ballast of the fluorescent tube, which is driven at 45 kHz. Although lock-in amplification is capable of differentiating the contributions from different modulation frequencies, as will be shown in Figure 6, the reduction of noise signal is paramount for a good measurement. Ambient light is just one possible source, but other electronics can also induce noise, which would then be superimposed onto the signal. Note that bias light is not always unwanted noise, but often bias light is applied on purpose to set the DUT into operating conditions.
In Figure 3B,C,E,F, we note further that the response of the DUT upon change of the irradiation intensity is delayed. These rise-time effects will be discussed in greater detail in the next section and originate here from two distinct effects: first, the steep increase and decrease of the DUT response upon the 2177.7-Hz modulation is delayed by the low-pass filter in the PA. Second, the signal continues to increase/decrease at slower time scales (e.g., visible between 0.68 and 0.80 ms in Figure 3C), which we attribute to the occupation kinetics of defect states in the solar cell.
(b) Pre-Amplification
The PA not only amplifies the modulated signal of the DUT but can significantly change its wave form. As detailed above, the contacts of the solar cell are such that a negative voltage is measured upon illumination. No bias light was added for the measurements shown in Figure 4.
The measurements were taken with increasing filter rise times to demonstrate their effects when amplification strength is held constant. In many cases, filter rise times are hardware-coupled to the amplification. The stronger the amplification is, the longer the response time is, and the smaller is the cut-off frequency of the low-pass filter in the PA36,37.
With a filter rise time of 10 µs as in the top panel of Figure 4, the signal is barely delayed, spans the nominal peak-to-peak range from roughly 10 mV to -65 mV, and reaches plateaus at the peak values. With 100 µs filter rise time, delay effects are visible in the modulated signal but the modulation is still distinct and the amplitude is in a similar range as for 10 µs. A filter rise time of 1 ms is longer than the period of the modulation (0.46 ms). Therefore, the modulation is suppressed to amplitudes below 10 mV and the shape reflects only the beginning of the rising and falling edge, which is obviously not suited for quantitative XBIC measurements. This connection between gain and filter rise time has to be kept in mind particularly for the combination of fast modulation frequencies,  , with strong amplification.
, with strong amplification.
(c) Signal Mixing
The key difference between standard signal amplification and lock-in amplification is the mixing of the DUT signal with a reference signal and the subsequent suppression of high frequencies by a low-pass filter.
The signal path for the mixing is depicted in Figure 5. For the discussion of the signal mixing, a few simplifications are made. The reference signal can be described as a sinusoidal signal
(6)  ,
,
where  is the amplitude and
is the amplitude and  is the modulation frequency of the reference signal. The modulated signal of the DUT fed into the LIA can be represented in a similar fashion as
is the modulation frequency of the reference signal. The modulated signal of the DUT fed into the LIA can be represented in a similar fashion as
(7)  ,
,
where  is the amplitude and
is the amplitude and  is the modulation frequency of the DUT signal, and
is the modulation frequency of the DUT signal, and  is a phase offset of the DUT signal to the reference signal.
is a phase offset of the DUT signal to the reference signal.
Following from (1) and (2), the mixed signal is:
(8)  .
.
The modulation frequency of the DUT is the reference frequency,  . Therefore, the trigonometric principle
. Therefore, the trigonometric principle
(9) 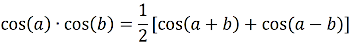
can be used to rewrite  as the sum of two terms with different frequencies:
as the sum of two terms with different frequencies:
(10)  .
.
The low-pass filter mitigates the fast signal  such that the lock-in amplified signal can be approximated38,39 as
such that the lock-in amplified signal can be approximated38,39 as
(11)  .
.
The DUT signal mixed with the reference signal is called the in-phase component  , and the DUT signal mixed with the 90 ° phase-shifted reference is called the quadrature component
, and the DUT signal mixed with the 90 ° phase-shifted reference is called the quadrature component  :
:
(12) 
(13)  .
.
From Eq. (12) and (13), the RMS amplitude
(14) 
as well as the phase
(15) 
of the mixed signal can be obtained with the two-argument arcus tangent function. Many LIA have an internal phase adjust to set  to zero during measurements.
to zero during measurements.
(d) Low-Pass Filter Frequency
Figure 6 shows the effect of bias light and different low-pass filter settings on the lock-in amplified RMS amplitude,  . We used a LIA that allowed us to record the signal resulting from different filter parameters simultaneously.
. We used a LIA that allowed us to record the signal resulting from different filter parameters simultaneously.
The cut-off frequency  of a low-pass filter defines the frequency, at which the signal is attenuated to 50%. While lower frequencies are transmitted, higher frequencies are suppressed. Figure 6A,E show the direct signal with
of a low-pass filter defines the frequency, at which the signal is attenuated to 50%. While lower frequencies are transmitted, higher frequencies are suppressed. Figure 6A,E show the direct signal with  = 466.7 kHz, which effectively does not eliminate noise or lower-frequency modulations but lets them pass with the raw signal. The conversion of the raw pre-amplified signal to the RMS amplitude
= 466.7 kHz, which effectively does not eliminate noise or lower-frequency modulations but lets them pass with the raw signal. The conversion of the raw pre-amplified signal to the RMS amplitude  leads to an additional factor of
leads to an additional factor of  for frequencies sufficiently below
for frequencies sufficiently below  . For example, a constant input voltage of
. For example, a constant input voltage of  is output as
is output as  .
.
Whereas the average offset in Figure 6E is negligible without bias light (in average 2 mV), it increases to an average of around 75 mV with bias light (Figure 6A). The difference is of comparable strength as between Figure 3A and Figure 3D, but beware that these were separate measurements. In both cases, turning on the chopping source leads to a significant increase in  , and the peak-to-peak variation of
, and the peak-to-peak variation of  corresponds to the peak-to-peak variation of the raw signal shown in Figure 3B and Figure 3E.
corresponds to the peak-to-peak variation of the raw signal shown in Figure 3B and Figure 3E.
In Figure 6B,F, the RMS amplitude  is displayed after using a low-pass filter with
is displayed after using a low-pass filter with  1000 Hz. Again an offset can be observed in Figure 6B due to the bias light, but the offset is smaller with around 18 mV on average. This offset is caused by the 100 Hz modulation of the fluorescent light, whereas the 90 kHz modulation is blocked by the low-pass filter. Furthermore, the noise level of the 'beam on' state is still significant with a peak-to-peak variation around 46 mV, while the average signal value amounts to 32 mV. Without bias light (Figure 6F) the peak-to-peak variation amounts to about 17 mV during 'beam on' with an average value of 23.5 mV. The average offset during 'beam off' is smaller than 0.5 mV. These measurements show that the combination of a low-pass filter with
1000 Hz. Again an offset can be observed in Figure 6B due to the bias light, but the offset is smaller with around 18 mV on average. This offset is caused by the 100 Hz modulation of the fluorescent light, whereas the 90 kHz modulation is blocked by the low-pass filter. Furthermore, the noise level of the 'beam on' state is still significant with a peak-to-peak variation around 46 mV, while the average signal value amounts to 32 mV. Without bias light (Figure 6F) the peak-to-peak variation amounts to about 17 mV during 'beam on' with an average value of 23.5 mV. The average offset during 'beam off' is smaller than 0.5 mV. These measurements show that the combination of a low-pass filter with  1000 Hz and a chopping frequency of
1000 Hz and a chopping frequency of  2177.7 Hz is not ideal: the signal carrying the modulation frequency is only partially removed but not entirely suppressed by the low-pass filter. The remaining part leads to significant peak-to-peak variations of
2177.7 Hz is not ideal: the signal carrying the modulation frequency is only partially removed but not entirely suppressed by the low-pass filter. The remaining part leads to significant peak-to-peak variations of  during the 'beam on' state. When bias light is present, the 100 Hz modulation due to net frequency of the fluorescence lamps further increases the peak-to-peak values.
during the 'beam on' state. When bias light is present, the 100 Hz modulation due to net frequency of the fluorescence lamps further increases the peak-to-peak values.
In Figure 6C,G, the influence of the bias light can be seen as minimal: the 10.27 Hz low-pass filter cuts off most noise and modulation of the fluorescent light, and a clear beam-induced signal can be extracted. Albeit hardly visible here, the offset and spread of noise are still slightly greater with bias light. This can be caused by stray light passing through the chopper wheel onto the DUT. Therefore, it is advisable to implement the chopper far upstream to avoid the modulation of stray light.
Figure 6D,H are a zoom into the change from 'beam on' to 'beam off' after 6 s in Figure 6B,C,F,G, respectively. The superimposed modulation at 100 Hz (fluorescence lamps frequency) is visible in Figure 6D for the low-pass filter with  1000 Hz. Note also the delay in the signal after the filter with
1000 Hz. Note also the delay in the signal after the filter with  10.27 Hz compared to the signal after the filter with
10.27 Hz compared to the signal after the filter with  1000 Hz, when the beam is turned off. Similar to the case for slow rise times of the PA, low
1000 Hz, when the beam is turned off. Similar to the case for slow rise times of the PA, low  of the low-pass filter in the LIA cause slower adaptation of
of the low-pass filter in the LIA cause slower adaptation of  to signal changes.
to signal changes.
Altogether, we have found that a low-pass filter with  10.27 Hz and a roll-off of 48 dB/oct (see next section) offers in this case the best compromise between fast scanning speed (in favor of high
10.27 Hz and a roll-off of 48 dB/oct (see next section) offers in this case the best compromise between fast scanning speed (in favor of high  values) and suppression of bias light or noise (in favor of low
values) and suppression of bias light or noise (in favor of low  values, most importantly below the grid frequency 50 Hz).
values, most importantly below the grid frequency 50 Hz).
(e) Low-Pass Filter Roll-off
As many digital lock-in amplifiers, the model that was used here employs so-called discrete-time RC filters or exponential running average filters whose characteristics are very close to those of an analog resistor-capacitor RC filter40. Apart from the filter cut-off frequency that has been discussed in the previous section, there is only one free parameter, the filter order  , that defines the slope of the cut-off as
, that defines the slope of the cut-off as  dB/oct.
dB/oct.
Figure 7A shows the effect of the filter order on the frequency-dependent attenuation for different cut-off frequencies that correspond to time constants  ms and
ms and  ms. Time constants between these two extremes are suitable for most XBIC measurements. The filter attenuation has been calculated40 in the frequency domain as the absolute value squared
ms. Time constants between these two extremes are suitable for most XBIC measurements. The filter attenuation has been calculated40 in the frequency domain as the absolute value squared  of the complex transfer function
of the complex transfer function
(16) 
as a function of the frequency  and a filter of order
and a filter of order  with a time constant
with a time constant  . Transfer functions of higher order filters are obtained by multiplication of the transfer functions of the serially connected individual filters. Similar to
. Transfer functions of higher order filters are obtained by multiplication of the transfer functions of the serially connected individual filters. Similar to  , we define
, we define  and
and  as the frequencies, at which the attenuation is 5% and 95%, respectively. The product of these frequencies and
as the frequencies, at which the attenuation is 5% and 95%, respectively. The product of these frequencies and  is constant and given in Table 1 for the conversion between the cut-off frequencies and the filter time constant.
is constant and given in Table 1 for the conversion between the cut-off frequencies and the filter time constant.
In the time domain, the filter response  for
for  is recursively calculated from an input signal
is recursively calculated from an input signal  that is defined at discrete times
that is defined at discrete times  ,
,  ,
,  , etc., spaced by the sampling time
, etc., spaced by the sampling time  :
:
(17) 
The response of filters with  is calculated by multiple iteration of Eq. 17 with
is calculated by multiple iteration of Eq. 17 with  calculated from
calculated from  and
and  . The filter response to an increasing (at time 0) and decreasing step function (at time
. The filter response to an increasing (at time 0) and decreasing step function (at time  ) is shown in Figure 7B for filter orders 1 to 8, as a function of the time in units of
) is shown in Figure 7B for filter orders 1 to 8, as a function of the time in units of  . Note that the response is delayed with respect to the input signal and that this delay increases with
. Note that the response is delayed with respect to the input signal and that this delay increases with  . The delay is quantified in Table 1 as the times
. The delay is quantified in Table 1 as the times  ,
,  , and
, and  , within which the transmitted signal reaches 5%, 50%, or 95%, respectively.
, within which the transmitted signal reaches 5%, 50%, or 95%, respectively.
The choice of the correct filter roll-off is as critical as of the cut-off frequency when designing the experiment. In application 1 presented in section (g), high-quality XBIC measurements have been obtained with a chopper frequency of 1177 Hz, dwell time of 100 ms, and cut-off frequency of 40 Hz at filter order 8. With the numbers from Table 1, this translates into  , and
, and  . This time is considerably shorter than the dwell time such that no delay-artifacts are introduced.
. This time is considerably shorter than the dwell time such that no delay-artifacts are introduced.
(f) Dwell Time Correction
In classical step-mode measurements, the scanning stage moves to the nominal position, and the start of the measurement at that pixel position is triggered after the precise position is reached. For short dwell times, the settling time becomes limiting for the overall scan time, which motivates so-called fly-scan or continuous measurement modes: there, the scan stage moves continuously, and the measurement data is attributed to pixels with the encoded stage position in post-processing. However, this can lead to additional issues as shown in Figure 8. In this case, the motors of the sample stage were not moving uniformly in the  direction, resulting in varying dwell times per pixel (see Figure 8A). The dwell-time variations directly translate into variations in XBIC measurements, as seen in Figure 8C. Therefore, the XBIC signal needs to be normalized to the dwell time, the results of which are shown in Figure 8D. Similarly, variations in beam intensity (displayed in Figure 8B) often need to be accounted for by normalization to the photon flux. XBIC signal normalized to the photon flux can be seen in Figure 8E; for minimal error on the absolute XBIC quantification, the photon flux itself has been normalized to its median value. Figure 8F shows the XBIC map normalized to the dwell time as well as to the photon flux, which reduced the impact of most measurement artifacts. Finally, Figure 8G shows the XBIC data after conversion from a count rate to the current using Eq. (1).
direction, resulting in varying dwell times per pixel (see Figure 8A). The dwell-time variations directly translate into variations in XBIC measurements, as seen in Figure 8C. Therefore, the XBIC signal needs to be normalized to the dwell time, the results of which are shown in Figure 8D. Similarly, variations in beam intensity (displayed in Figure 8B) often need to be accounted for by normalization to the photon flux. XBIC signal normalized to the photon flux can be seen in Figure 8E; for minimal error on the absolute XBIC quantification, the photon flux itself has been normalized to its median value. Figure 8F shows the XBIC map normalized to the dwell time as well as to the photon flux, which reduced the impact of most measurement artifacts. Finally, Figure 8G shows the XBIC data after conversion from a count rate to the current using Eq. (1).
(g) Application 1: XBIC of a Solar Cell with Bias Voltage and XRF
Figure 9A-B shows the impact of lock-in amplification on the signal-to-noise ratio in X-ray beam induced current measurements. The noisiness of the direct signal is apparent in Figure 9A: strong intensity contrasts from line to line are indicative of measurement artifacts, and fine XBIC variations from the DUT get buried in the arbitrarily changing signal. On the other hand, these fine features are clearly visible in Figure 9B. Note that the noise level in Figure 9A is unusually high for unknown reasons despite the optimization of the setup prior to the measurements. In such cases, the signal-to-noise ratio improvement by lock-in amplification is dramatically higher than in cases of already high signal-to-noise ratio with standard amplification (e.g., application 3 in section (i)), where lock-in amplification would only lead to marginal improvements.
With the PA, forward (Figure 9C) and reverse (Figure 9D) bias voltages of -50 mV and +50 mV, respectively, were applied to the sample and the area of Figure 9A-B rescanned. The dominant features visible in Figure 9B are still visible in Figure 9C and Figure 9D, but they are less distinct as the maps are noisier. This is because the application of bias voltage or bias light induces a direct current that is often orders of magnitude larger than the modulated XBIC signal. Ultimately, the ratio of direct to modulated signal limits the applicability of lock-in amplification. Despite the poor signal-to-noise ratio, it is worth pointing out that lock-in amplification enables mapping of the solar cell performance at the nanoscale with bias voltage and bias light applied, which would hardly be possible otherwise30.
As the performance of the CIGS solar cell is correlated to the absorber layer composition7,41, we measured the XRF signal simultaneously with the XBIC. In Figure 9E-F, the concentrations of Ga and In are presented. Both elements are part of the absorber layer and their ratio is deemed to be of great influence to the performance of the solar cell7. The statistics of Ga are much greater than for In, which is due to the higher absorption coefficient and less self-absorption at the excitation energy of 10.4 keV. Due to the low statistics, features in the In map are almost invisible, whereas the Ga concentration is clear enough to be correlated with the electrical performance in Figure 9B. For a higher In signal, one could either choose longer dwell times or choose an absorption energy with larger In absorption cross section. This illustrates the importance of a sufficiently long dwell time as well as the tailoring of the beam energy to the elements of interest.
With long dwell times and large maps, another point has to be kept in mind: during measurements spanning multiple hours, sample drift can become a critical issue. Thermal fluctuations (particularly after sample change or large motor movements with poor heat dissipation) and the instability of mechanical stage components often lead to sample drift as can be seen by comparing the vertical positions of Figure 9D and Figure 9B.
(h) Application 2: XBIC of a Solar Cell with XBIV and XRF
Figure 10 shows a multi-modal scan of a CIGS solar cell, where the cell is operated under short-circuit condition measuring XBIC in Figure 10A, and under open-circuit condition measuring XBIV in Figure 10B. The XRF measurement shown in Figure 10C was taken simultaneously with the XBIV measurement. To collect enough XRF counts, the dwell time per pixel was 0.5 s for Figure 10B-C as compared to 0.01 s in Figure 10A. Accordingly, a lower cut-off frequency in the low-pass filter for the XBIV measurement could be used compared to the XBIC measurement (10.27 Hz vs. 501.1 Hz, both with roll-off 48 dB/oct). For XBIV measurements alone, we could have used the same dwell time and low-pass filter settings as for the XBIC measurement with similar signal-to-noise ratio. However, it was overall more time-efficient to combine XBIV with XRF measurements with the XRF measurement governing the dwell time, than performing separate XBIV and XRF measurements.
Comparing Figure 10A, and Figure 10B, we note that the short-circuit current  , measured as XBIC, and the open circuit voltage
, measured as XBIC, and the open circuit voltage  , measured as XBIV, are correlated: large high- and low-performing areas are visible in both measurement modes. This indicates that local thickness variations and/or recombination dominate the performance here, rather than bandgap variations, which would lead to opposite trends in XBIC and XBIV28.
, measured as XBIV, are correlated: large high- and low-performing areas are visible in both measurement modes. This indicates that local thickness variations and/or recombination dominate the performance here, rather than bandgap variations, which would lead to opposite trends in XBIC and XBIV28.
Further, taking Figure 10C into account, one can see that certain areas with low performance such as at  correlate with low Cu count rate, whereas performance is not correlated with the Cu count rate in other areas.
correlate with low Cu count rate, whereas performance is not correlated with the Cu count rate in other areas.
(i) Application 3: XBIC and XRF of a Nanowire
Beyond solar cells, contacted nanowires24 or nano-sheets, as well as quantum dots, are other examples of DUT that can profit from lock-in amplified XBIC measurements. For demonstration, Figure 11A shows the elemental distribution from XRF measurements, and Figure 11B the corresponding XBIC map of a CdS nanowire. The two contacts made of Pt and the CdS wire are clearly distinguishable, and the XBIC signal shows a matching electrical response. Particularly noteworthy is the fact that XBIC can unveil the electrical performance of the nanowire underneath the Pt contact, which is unique to X-ray nanoprobes and attributable to the high penetration depth of hard X-rays. The complementation of material composition and electrical properties of the nanowire exemplarily demonstrates the advantages of multi-modal X-ray measurements.

Figure 1: Setup for lock-in amplified X-ray beam induced current (XBIC) measurements on a device under test (DUT). The beam path is depicted in red. The green forms indicate optional X-ray fluorescence (XRF) and area detectors for multi-modal measurements, yellow indicates optional bias light. Hardware components for XBIC measurements are colored black, while XBIC signal paths are blue with signal outputs and inputs shown as filled and empty circles, respectively. Before the data acquisition (DAQ), the DC (direct current) and AC (alternating current) signal is converted from a voltage to a frequency (V2F). For alternative signal paths we refer to part (a) of the discussion section. Please click here to view a larger version of this figure.

Figure 2: Example of a kinematic sample holder optimized for multimodal X-ray microscopy measurements including X-ray beam induced current. Thin copper wires are mounted onto the front and back contacts of a Cu(In,Ga)Se2 (CIGS) solar cell with silver paint, and connected to the PCB contacts. Polyimide tape is used to separate the wires, avoiding short-circuiting of the sample. Please click here to view a larger version of this figure.

Figure 3: Pre-amplified solar cell response upon irradiation with bias light and modulated beam. Top row without bias light, bottom row with bias light: A & D - beam off; B & E - beam on; C & F - zoom into the red rectangle of B & E. Please click here to view a larger version of this figure.

Figure 4: Solar cell response after pre-amplification with three different filter rise times (10 µs - blue, 100 µs - red, 1 ms - green) in the pre-amplifier. Please click here to view a larger version of this figure.

Figure 5: Signal processing by the lock-in amplifier31.  is the signal input from the DUT and
is the signal input from the DUT and  is the reference signal from the chopper. Please click here to view a larger version of this figure.
is the reference signal from the chopper. Please click here to view a larger version of this figure.

Figure 6: Lock-in amplified RMS amplitude  with low-pass filter cut-off frequencies
with low-pass filter cut-off frequencies  466.7 kHz (blue),
466.7 kHz (blue),  1 kHz (purple),
1 kHz (purple),  10.27 Hz (red), and constant filter roll-off 48 dB/oct. The DUT was a Cu(In,Ga)Se2 solar cell with (A, B, C, D) and without (E, F, G, H) bias light applied. The times when the chopped photon beam was turned on and off are indicated in the figures as vertical dashed lines. Please click here to view a larger version of this figure.
10.27 Hz (red), and constant filter roll-off 48 dB/oct. The DUT was a Cu(In,Ga)Se2 solar cell with (A, B, C, D) and without (E, F, G, H) bias light applied. The times when the chopped photon beam was turned on and off are indicated in the figures as vertical dashed lines. Please click here to view a larger version of this figure.

Figure 7: Effect of low-pass filter settings in the lock-in amplifier. A - Attenuation by the low-pass filter in the frequency domain for two time constants ( ms and
ms and  ms) and for filter orders 1 to 8. B - Transmitted signal response of the low-pass filter in the time domain, in units of the time constant
ms) and for filter orders 1 to 8. B - Transmitted signal response of the low-pass filter in the time domain, in units of the time constant  , for filter orders 1 to 8 upon step-like change of the input signal from 0 to 1 at time 0 and from 1 to 0 at time
, for filter orders 1 to 8 upon step-like change of the input signal from 0 to 1 at time 0 and from 1 to 0 at time  . Please click here to view a larger version of this figure.
. Please click here to view a larger version of this figure.

Figure 8: Fly-scan measurement of a Cu(In,Ga)Se2 solar cell at beamline P06 at PETRA III, taken at 15.25 keV photon energy with a focused flux of about  ph/s. The PA was used with
ph/s. The PA was used with  = 106 V/A, and the LIA with
= 106 V/A, and the LIA with  Hz (48 dB/oct). A - dwell time, B - photon flux, C - X-ray beam induced current (XBIC); XBIC map normalized to: D - dwell time, E - photon flux normalized to its median value, F - dwell time and normalized photon flux. G – normalized XBIC signal after conversion from the count rate to the current using Eq. (1). Please click here to view a larger version of this figure.
Hz (48 dB/oct). A - dwell time, B - photon flux, C - X-ray beam induced current (XBIC); XBIC map normalized to: D - dwell time, E - photon flux normalized to its median value, F - dwell time and normalized photon flux. G – normalized XBIC signal after conversion from the count rate to the current using Eq. (1). Please click here to view a larger version of this figure.

Figure 9: X-ray beam induced current (XBIC) and X-ray fluorescence (XRF) measurements of a Cu(In,Ga)Se2 solar cell, taken at the beamline ID16B at the European Synchrotron Radiation Facility with a focused flux on the order of  ph/s. The PA was used with
ph/s. The PA was used with  V/A, the LIA with
V/A, the LIA with  Hz (48 dB/oct). The beam energy was 10.4 keV, the chopper frequency was 1177 Hz, and the low-pass filter cut off at 40 Hz. The dwell time was 100 ms and the pixel size was 40 nm x 40 nm. The maps A, B, E and F were all taken at the same time; C and D are retakes after 50 min and 113 min, with 50 mV forward and reverse bias voltage applied, respectively. Please click here to view a larger version of this figure.
Hz (48 dB/oct). The beam energy was 10.4 keV, the chopper frequency was 1177 Hz, and the low-pass filter cut off at 40 Hz. The dwell time was 100 ms and the pixel size was 40 nm x 40 nm. The maps A, B, E and F were all taken at the same time; C and D are retakes after 50 min and 113 min, with 50 mV forward and reverse bias voltage applied, respectively. Please click here to view a larger version of this figure.

Figure 10: Multi-modal measurement of a Cu(In,Ga)Se2 solar cell, taken at beamline P06 at PETRA III with a focused flux of about  ph/s. The beam energy was 15.25 keV, the chopper frequency was 8015 Hz, and the pixel size 50 nm x 50 nm. A - X-ray beam induced current (XBIC) measured with a dwell time of 0.01 s, a PA with
ph/s. The beam energy was 15.25 keV, the chopper frequency was 8015 Hz, and the pixel size 50 nm x 50 nm. A - X-ray beam induced current (XBIC) measured with a dwell time of 0.01 s, a PA with  = 106 V/A, and a LIA with
= 106 V/A, and a LIA with  Hz (48 dB/oct); B - X-ray beam induced voltage (XBIV) covering the same area as panel A, measured with a dwell time of 0.5 s and a LIA with
Hz (48 dB/oct); B - X-ray beam induced voltage (XBIV) covering the same area as panel A, measured with a dwell time of 0.5 s and a LIA with  Hz (48 dB/oct); C - Cu count rate from an X-ray fluorescence (XRF) measurement, taken simultaneously with the XBIV measurement. Please click here to view a larger version of this figure.
Hz (48 dB/oct); C - Cu count rate from an X-ray fluorescence (XRF) measurement, taken simultaneously with the XBIV measurement. Please click here to view a larger version of this figure.

Figure 11: Multi-modal measurement of a CdS nanowire with Pt contacts, taken at beamline 26-ID-C of the Advanced Photon Source with a beam energy of 10.6 keV. A - Pt and Cd distribution from an X-ray fluorescence measurement. B - X-ray beam induced current (XBIC) measurement taken simultaneously with the XRF measurement, without lock-in amplification. Please click here to view a larger version of this figure.

Table 1: For discrete-time RC filters of orders 1 to 8, the product of the time constant and the frequency, at which the signal is attenuated by 5% ( ), 50% (
), 50% ( ), and 95% (
), and 95% ( ), is constant and given in the top part. In the lower part, the time delay is given, within which the signal reaches 5% (
), is constant and given in the top part. In the lower part, the time delay is given, within which the signal reaches 5% ( ), 50% (
), 50% ( ), and 95% (
), and 95% ( ), in units of the time constant
), in units of the time constant  and of the inverse cut-off frequency
and of the inverse cut-off frequency  . Please click here to download this excel file.
. Please click here to download this excel file.
| XBIC | EBIC | LBIC | |
| Multi-modal capability | ++ | + | + |
| Spatial resolution | ++ | ++ | - |
| Penetration depth | ++ | -- | + |
| Availability | -- | - | + |
| Sample damage | - | -- | ++ |
Table 2: Qualitative assessment of X-ray beam induced current (XBIC), electron beam induced current (EBIC) and laser beam induced current (LBIC).
Discussion
In this chapter, we discuss first the relevance of general XBIC measurement settings with respect to noise (a) and scanning speed (b). Next, we put XBIC measurements into the context of multi-modal measurements and discuss aspects of X-ray beam induced damage (c) and specific challenges related to simultaneous measurements of multiple parameters (d). Finally, we compare XBIC measurements with related measurements using electron- and laser-beams as probes (e).
(a) Noise and Error
Although lock-in amplification enables a higher signal-to-noise ratio compared to direct amplification, it is critical to avoid the introduction of noise at all levels as has been repeatedly stressed throughout this manuscript. For further discussion, we refer to literature discussing the measurement of small electrical signals42,43,44,45. Although state-of-the-art lock-in amplifiers are based on digital signal processing today, most strategies to reduce noise using analog lock-in amplifiers still apply.
Summarizing, it should be kept in mind that cables are prone to act as antennae and thus introduce noise into the system. This is particularly true in the environment of X-ray nanoprobes, where strong electro-magnetic fields are often unavoidable, their sources may even remain unknown. As a consequence, cables should be kept as short as possible and oriented such that the induced noise level is minimized. Extra shielding of the signal cables may further reduce the noise level.
The proper contacting of the DUT is equally important for noise minimization. A clean and robust method with small contact points is wire bonding. For TF solar cells, this does not always work due to adhesion issues. Alternatively, conductive tape based on graphite, copper, or aluminum is suited for larger samples. In many cases, the best results are obtained with manual application of silver paint to contact thin copper, gold, or platinum wires to the device. While tape and graphite paste might not give the best contact, silver paint can easily short circuit the device and has to be deposited with utmost care. Polyimide tape can be used to prevent short-circuiting of front and back contact.
Note that the cabling layout from contacting to signal transport needs to be adapted to beamline-specific boundary conditions. For example, the layout depicted in Figure 1 with the pre-amplified signal being split to the LIA and to the V2F converters is risky, if the V2F converters are located outside of the hutch. In this case, the long cable between pre-amplifier and V2F converter can catch noise that is transferred to the LIA. Therefore, we distinguish three cases of common signal paths for XBIC or XBIV measurements:
Case A: XBIC is measured with a pre-amplifier, and the DC/AC signal is split after the PA as depicted in Figure 1. In this case, a current offset can be applied in the PA such that the signal is always positive, avoiding the need of recording the positive and negative signal via two separate V2F converters. As a drawback, this would reduce the available voltage acceptance range in the LIA and lead to reduced sensitivity.
Case B: Avoiding the splitting of the pre-amplified signal, which is only input to the LIA, an additional demodulator can be used in the LIA with a low-pass filter at the maximum value (i.e. not locking in to the modulation frequency) such that the pre-amplified signal can be effectively output to the DAQ unit as demonstrated in Figure 6A,E. In this case, a voltage offset on the output can be applied to both the AC and DC signal, avoiding the need of recording the positive and negative signal via two separate V2F converters. This has no major drawbacks apart from a reduction of the available frequency range of the V2F, which is rarely limiting.
Case C: XBIV is measured and the DC/AC signal is split between the DUT and the lock-in amplifier. In this case, no voltage offset on the DC signal can be applied without applying an unwanted bias voltage on the DUT, such that always two separate V2F converters are required for the positive and negative signal parts.
In all cases, where the negative and positive parts of a signal are recorded via two different V2F converters, the total XBIC or XBIV signal is obtained as the difference between the positive and negative channel. If a LIA with two or more demodulators is available, we typically prefer case B, as it minimizes the wiring of the raw signal and allows easy switching between XBIC and XBIV measurements.
The error of XBIC measurements highly depends on the equipment and settings used such that no error quantification can be given here. The absolute error is higher than one might expect because of experimental and systematic errors. This is particularly true if the XBIC signal is converted to charge collection efficiency by scaling with a constant as described in the protocol. For example, the empiric relation between bandgap and ionization energy described by α (see Eq. 4) suffers from significant scatter; photon flux measurements are often not available with absolute errors below 10%; and the nanoscopic structure of the DUT is poorly known. However, we emphasize that the strength of lock-in amplified XBIC and XBIV measurements lies in the great relative accuracy within maps or comparable measurements.
(b) Scanning Speed
In many measurement modes that are based on photon detection such as XRF or X-ray scattering, the signal intensity increases in first approximation linearly with the acquisition time, with accordingly increased signal-to-noise ratio. This is not true for XBIC measurements, where the window of possible scanning speeds is not dictated by count statistics but by more complex considerations such as carrier dynamics and device structure.
Nevertheless, slow measurements with many periods of modulated signal per pixel typically lead to the best signal-to-noise ratio in lock-in amplified XBIC measurements, and oversampling with smoothening during post-processing (e.g. by binning or applying filters) can further reduce noise levels if measurement time allows. However, apart from throughput considerations, further constraints can set lower limits to the measurement speed, including: (1) X-ray beam induced degradation (see the following section), or environment-induced sample changes during in-situ measurements often reduce the allowable dwell time. (2) Sample drift and reproducibility of stage movements can be limiting, particularly for measurements at the nanoscale. (3) Variations of the electromagnetic noise level may be outrun by faster measurements. (4) Whereas photon-counting measurements can easily be normalized to the incident photon flux, the XBIC signal (and even more so the XBIV signal) is only to some extent linear to the incident photon flux28. Therefore, normalization to the photon flux only compensates part of the effects from photon-flux variation, and one should avoid taking XBIC measurements (such as maps or time-series) while the flux is varied. This is particularly an issue when the storage ring is filled during an XBIC map.
If the XBIC measurement speed is not governed by other measurement modes (see section (d)), XBIC measurements are typically taken with the maximum speed that provides satisfying signal-to-noise ratio. Upper limits to the measurement speed are given by the following constraints: (1) A fundamental upper limit to the measurement speed is the response time of the DUT. Ultimately, the response time is limited by the charge-collection time. For most thin-film solar cells with charge-carrier lifetimes in the nano- or microsecond range, this is uncritical, but this has to be kept in mind for high-quality crystalline-silicon solar cells with lifetimes of several milliseconds. However, capacitance effects can increase the response time also of TF solar cells such that it can limit the measurement speed. (2) Rotating chopper blades that are used to modulate the X-ray beam have upper speed limits. Depending on their location in the X-ray beam, the beam size may be up to 1 mm wide, which defines the minimum period of the blade. If the chopper is operated in vacuum, the rotation frequency is rarely limiting, matching in some cases even the electron-bunch frequency. However, the operation of choppers at such speeds in vacuum is challenging, such that most choppers are operated in air. In this case, the rotating speed is limited by mechanical vibrations and ultimately by the speed of the outmost part of the blade that needs to be smaller than the speed of sound. In our experience, the chopping frequency is limited often to ~ 7000 Hz in air. (3) In many cases, the response time of the PA sets the upper limit of the measurement speed. As shown in Figure 4, fast rise times of the PA are required to translate the signal modulation from the chopper. For large amplification, low-noise current amplifiers are used, which have rise times up to 100 ms. With such rise times, the chopping frequency can be limited to few Hz, which would require dwell times of several seconds. Therefore, the best strategy is often to choose a lower amplification by the PA with a faster response time that matches the chopping frequency. Although this translates into smaller signal-to-noise levels after pre-amplification, lock-in amplification can often still retrieve a high-quality modulated signal.
As an example, the used PA provides a bandwidth of more than 10 kHz for amplification in the µA/V range, even for the low-noise setting37. This allows chopping at the kHz range and measurement speeds up to the 100-Hz range with a low-pass filter with a cut-off frequency between the scanning and chopping frequency. These are measurement conditions we often utilize.
To avoid measurement artifacts, it is critically important to analyze the signal along the amplification chain: whereas limitation by the low-pass filter of the LIA can easily be detected as line-artifacts in maps (smearing out of the XBIC signal across several pixels), the system response of the DUT and PA requires inspection of the signal by a scope, which can be integrated in the LIA.
(c) Beam Damage
X-ray beam induced damage is a common issue and has been discussed for many systems, from biological samples to silicon solar cells and detectors46,47. Although inorganic semiconductors are generally more robust against X-ray irradiation compared to organic semiconductors or biological systems, X-ray beam induced damage is common also in thin-film solar cells. Specifically, we have observed X-ray beam induced damage of solar cells with CdTe, CIGS29, perovskite18, and organic absorber layers. Note that the electronic response of DUT like solar cells is sensitive to defect concentrations below the ppm level, where charge-carrier recombination affects the performance without apparent chemical damage.
Therefore, it is generally required to test the sensitivity of a DUT to beam damage. In practice, we evaluate the X-ray beam induced degradation of any DUT prior to actual XBIC measurements, and establish conditions that allow measurements to be the least influenced by degradation effects.
Different strategies exist to cope with X-ray beam induced damage, but what they all have in common is that they aim to reduce the radiation dosage at a measurement spot prior to the evaluation of the performance there. In other words, the objective is to outrun degradation following the paradigm "measure faster than the DUT degrades". The strategies include: (1) Use short dwell times. (2) Increase the step size, reducing the measurement resolution. (3) Reduce the X-ray beam intensity by attenuation filters. Depending on the beamline and DUT, different approaches may be chosen or a combination thereof. For instance, the lack of fast shutters or fly-scan modes exclude (1), and wide-spread X-ray beam profiles such as those generated by zone plates can lead to significant degradation far away from the central beam position.
Fortunately, most degradation mechanisms only lead to locally enhanced charge carrier recombination. This limits the lateral effect of the degradation to the diffusion length of the charge carriers, and XBIC measurements further away from the degraded areas remain nearly unaffected. If, instead, degradation mechanisms lead to local shunting of the DUT, further XBIC measurements would be seriously hampered. To keep the deposited radiation dosage to a minimum, the critical measurements should be performed first on a fresh spot and then afterwards, photon-hungry methods, like XRF, that are more indifferent to beam damage, may be utilized in the same location.
(d) Multi-Modal Measurements
The compatibility of XBIC with further measurement modes enables direct point-by-point correlation of the electrical performance with simultaneously assessed parameters23. Here, we shortly discuss the combination of XBIC measurements with XBIV, XRF, SAXS, WAXS, and XEOL measurements. The combination with further measurement modes such as electron yield or holography can easily be imagined, but these modes are not generally compatible with the setups or modes of the scanning measurements.
Even if the geometrical arrangement of detectors and samples for simultaneous measurement of XBIC, XBIV, XRF, SAXS, WAXS, and XEOL is possible, there are fundamental and practical aspects prohibiting the simultaneous assessment of all modes.
(1) The state of the solar cell prohibits the simultaneous measurement of XBIC (short circuit) and XBIV (open circuit) measurements. As XEOL48,49 measures the radiative recombination of electron-hole pairs, a measured current of the solar cell (XBIC) would be a competitive process. Therefore, XEOL measurements are typically conducted under open-circuit condition, which is compatible with simultaneous XBIV measurements.
(2) If beam damage is an issue for XBIC or XBIV measurements, they may not be combined with photon-hungry techniques such as XRF or XEOL. As a rule of thumb, beam damage effects are first visible in the electrical (XBIC & XBIV) and the optical (XEOL) performance, being sensitive to charge-carrier recombination via electronic defects. Second, structural damage occurs (visible in SAXS & WAXS), followed by compositional modification visible in XRF.
(3) Although chopping the X-ray beam is generally compatible with all measurement modes, it can lead to artifacts: first, the integrated photon flux per pixel varies by the integrated flux passing the chopper wheel in one period. This effect becomes larger with a smaller ratio between the chopping and the scanning frequency. Second, the interaction between the chopper wheel and the X-ray beam can lead to scattered, diffracted, and fluorescent photons. Third, the integrated photon flux is reduced by 50%, which is particularly critical for photon-hungry measurement modes.
As a consequence of these considerations, the ideal measurement scheme depends on the given DUT and prioritization of measurement modes. However, it is often wise to start with a measurement optimized for XBIC. If lock-in amplified XBIV is required, this is typically the second scan. Otherwise, the chopper can be removed, and all other measurements, including standard XBIV, can be performed with longer dwell time as required for the most photon-hungry technique. Ideally, XRF data are measured during all scans, which allows for image registration in post-processing to account for sample drift.
(e) Different Probes for Beam-Induced Measurements
There are alternative probes to X-ray beams for the assessment of the spatially resolved electrical performance of a DUT with specific advantages and disadvantages. Therefore, a qualitative comparison of XBIC with electron-beam induced current (EBIC) and laser-beam induced current (LBIC) as measured in electron microscopes or with optical setups is given in Table 2.
The electron-hole pair generation by a laser comes closest to the outdoor operation of solar cells. However, the spatial resolution of LBIC is fundamentally limited by the wavelength of the laser. EBIC measurements offer a greater spatial resolution that is typically limited by the interaction radius of the electron beam with the DUT. The main drawback of EBIC measurements is their surface sensitivity, hindering the assessment of the absorber layer performance through the layer stack or even in encapsulated devices. Furthermore, uneven surfaces of the DUT in combination with non-linear secondary-electron emission effects often lead to distorted EBIC results. In contrast, XBIC measurements hardly suffer from topological variations, as most signal is generated deep in the bulk material and surface-charge effects are mitigated by proper grounding.
All three beam-induced techniques have in common that charge injection is highly inhomogeneous, peaking at the beam position. As a consequence, the excess carrier concentration and current density are inhomogeneously distributed. In a simplified picture, the majority of the solar cell operates in dark, and a small spot operates at a high injection level that can reach hundreds of sun equivalents for focused beams. The injection-level distribution depends not only on the beam size and shape, but also on the beam energy, device stack, and time structure of the injection. So far, the X-ray beam has been treated as a continuous beam, which is justified for charge-carrier collection processes that are slower than microseconds. However, synchrotron-sourced X-rays consist of sub-100-ps pulses with intensities and pulse frequency depending on the storage-ring fill pattern. Although we have not noticed any impact of the fill pattern on comparably slow XBIC measurements, the short-term injection level does depend on it. In contrast, one can make use of the time structure of X-rays: similar as has been demonstrated for time-resolved XEOL21, one can imagine time-resolved XBIC or XBIV measurements, or locking the XBIC/XBIV signal into the electron-bunch frequency.
An adequate discussion of the consequences of inhomogeneous injection levels requires full 3D simulation of all relevant beam and device parameters including the convolution of the time-dependent injection level with the 3D mobility and lifetime in the DUT, which is beyond the scope of this manuscript. However, it is conceptually the same for all beam-induced current and voltage measurements and we refer to the literature discussing the injection-level dependence of EBIC50 and LBIC51 measurements.
The negative consequences of local charge injection can experimentally be mitigated by the application of bias light with the intensity of 1 sun equivalent, and beam-induced excitation adding only a negligible amount of excess charge carriers. In practice, this concept is technologically limited by the dynamic reserve of 100-120 dB in state-of-the-art lock-in amplifiers, which corresponds to a signal-to-noise ratio of 105 to 106. While this suffices for devices of size comparable to the beam size, it does not allow the application of bias light at relevant levels for macroscopic devices. The obvious solution is to decrease the sample size. Unfortunately, this is often limited by electrical border effects up to several hundred micrometers off the sample border or contact points.
Note also that one can make use of the injection-level dependence of XBIC measurements: similar to EBIC and LBIC, performing injection-level series by varying the X-ray beam intensity can unveil information about dominant recombination mechanisms and charge carrier diffusion52,53.
In conclusion, the penetration depth of X-rays combined with the high spatial resolution makes XBIC the most fitting technique to study DUT with buried structures such as TF solar cells in a correlative microscopy approach. The interaction radius of XBIC measurements is typically smaller than for EBIC, and the spatial resolution is often limited by the diffusion length of the charge carriers. The main drawback of XBIC measurements is the limited availability of X-ray nanoprobes.
Disclosures
The authors have nothing to disclose.
Acknowledgments
We greatly acknowledge J. Garrevoet, M. Seyrich, A. Schropp, D. Brückner, J. Hagemann, K. Spiers, and T. Boese from the Deutsches Elektronen-Synchrotron (DESY) and A. Kolditz, J. Siebels, J. Flügge, C. Strelow, T. Kipp, and A. Mews from the University of Hamburg for supporting measurements at beamline P06 at PETRA III, DESY; M. Holt, Z. Cai, M. Cherukara, and V. Rose from the Argonne National Laboratory (ANL) for supporting measurements at beamline 26-ID-C at the Advanced Photon Source (APS) at ANL; D. Salomon and R. Tucoulou from the European Synchrotron Radiation Facility (ESRF) for supporting measurements at beamline ID16B at ESRF; R. Farshchi, D. Poplavkyy, and J. Bailey from MiaSolé Hi-Tech Corp., and E. Avancini, Y. Romanyuk, S. Bücheler, and A. Tiwari from the Swiss Federal Laboratories for Materials Science and Technology (EMPA) for providing solar cells. We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. We acknowledge the European Synchrotron Radiation Facility (Grenoble, France) for provision of synchrotron radiation facilities. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357.
Materials
| Name | Company | Catalog Number | Comments |
| BNC cabling and connectors | From generall cable suppliers | ||
| Chopper blade | Thorlabs | MC1F10HP | Apart from technical compatibility of the chopper wheel with the chopper system, it should be checked that the chopper blade sufficiently blocks the X-ray beam. |
| Conductive silver paint | Conrad | 530042 | Alternative products can be obtained from Pelco and others |
| Copper wires | From cable suppliers for contacting of the solar cell | ||
| Current Preamplifier | Standford | SR570 | Alternatives include the Keithley 487 or 6487 Picoammeter. |
| Device under test (DUT) | Suitable device for XBIC measurements. | ||
| Holder with printed circuit board | Custom design | ||
| Kinematic sample mount | Thorlabs | KB25/M | Optional, allows easy positioning and changing of sample. Alternatives include the M-BK-1A from Newport |
| Lock-in Amplifier | Zurich Instruments | UHFLI or MFLI | Whereas the MFLI has current preamplifiers included, the UHFLI requires an external current preamplifier but offers more options. Therefore, the UHFLI was used for the presented experiment. |
| Measurement control/data acquisition unit | Available at different synchrotrons. | ||
| Optical Chopper | Thorlabs | MC2000B(-EC) | Alternatives include the choppers SR540 from Stanford Research Systems, or model 3502 from Newport. |
| Polyimide tape | Rolls with different widths and thicknesses are available | ||
| X-ray source | Available at different synchrotrons |
References
- Hales, D. DREN21. Renewables 2018-global status report, Paris, REN21 Secretariate; 2018. , (2018).
- Jäger-Waldau, A. Snapshot of photovoltaics - February 2018. EPJ Photovoltaics. 9, 6 (2018).
- Haegel, N. M., et al. Terawatt-scale photovoltaics: Trajectories and challenges. Science. 356, 141-143 (2017).
- Polman, A., Knight, M., Garnett, E. C., Ehrler, B., Sinke, W. C. Photovoltaic materials: Present efficiencies and future challenges. Science. 352, (2016).
- Cao, Q., et al. Defects in Cu(In,Ga)Se 2 chalcopyrite semiconductors: A comparative study of material properties, defect states, and photovoltaic performance. Advanced Energy Materials. 1, 845-853 (2011).
- Abou-Ras, D., et al. Compositional and electrical properties of line and planar defects in Cu(In,Ga)Se2 thin films for solar cells - a review. Physica Status Solidi - Rapid Research Letters. 10, 363-375 (2016).
- West, B. M., et al. Grain Engineering: How Nanoscale Inhomogeneities Can Control Charge Collection in Solar Cells. Nano Energy. 32, 488-493 (2017).
- Jackson, P., et al. Properties of Cu(In,Ga)Se2solar cells with new record efficiencies up to 21.7%. Physica Status Solidi - Rapid Research Letters. 9, 28-31 (2015).
- Rau, U. Electrical characteristics of CIGS thin film solar cells and the role of defects for device performance. Solar Energy Materials and Solar Cells. 67, 137-143 (2001).
- Jordan, D. C., Kurtz, S. R. Photovoltaic Degradation Rates - an Analytical Review. Progress in Photovoltaics: Research and Applications. 21, 12-29 (2013).
- Bailey, J., Zapalac, G., Poplavskyy, D. Metastable defect measurement from capacitance-voltage and admittance measurements in Cu(In,Ga)Se2 solar cells. 2017 IEEE 44th Photovoltaic Specialist Conference, PVSC 2017. , 1-6 (2018).
- Abou-ras, D., Kirchartz, T., Rau, U. Advanced Characterization Techniques for Thin Film Solar Cells. , Wiley-VCH Verlag GmbH&Co. KGaA. (2011).
- Schroer, C. G., et al. X-ray nanoprobe at beamline P06 at PETRA III. Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 616, 93-97 (2010).
- Winarski, R. P., et al. A hard X-ray nanoprobe beamline for nanoscale microscopy. Journal of Synchrotron Radiation. 19, 1056-1060 (2012).
- Martinez-Criado, G., et al. ID16B: A hard X-ray nanoprobe beamline at the ESRF for nano-analysis. Journal of Synchrotron Radiation. 23, 344-352 (2016).
- Nazaretski, E., et al. Design and performance of an X-ray scanning microscope at the Hard X-ray Nanoprobe beamline of NSLS-II. Journal of Synchrotron Radiation. 24, 1113-1119 (2017).
- West, B. M., et al. X-ray fluorescence at nanoscale resolution for multicomponent layered structures: A solar cell case study. Journal of Synchrotron Radiation. 24, 288-295 (2017).
- Stuckelberger, M., et al. Charge Collection in Hybrid Perovskite Solar Cells: Relation to the Nanoscale Elemental Distribution. IEEE Journal of Photovoltaics. 7, 590-597 (2017).
- Chayanun, L., et al. Nanoscale mapping of carrier collection in single nanowire solar cells using X-ray beam induced current. Journal of Synchrotron Radiation. 26, 102-108 (2019).
- Martínez-Criado, G., et al. Probing quantum confinement within single core-multishell nanowires. Nano Letters. 12, 5829-5834 (2012).
- Martínez-Criado, G., et al. Exploring single semiconductor nanowires with a multimodal hard X-ray nanoprobe. Advanced Materials. 26, 7873-7879 (2014).
- Ulvestad, A., et al. Multimodal x-ray imaging of grain-level properties and performance in a polycrystalline solar cell. Accepted for publication in the Journal of Synchrotron Radiation. , (2019).
- Stuckelberger, M., et al. Engineering solar cells based on correlative X-ray microscopy. Journal of Materials Research. 32, 1825-1854 (2017).
- Chayanun, L., et al. Spectrally resolved x-ray beam induced current in a single InGaP nanowire. Nanotechnology. 29, (2018).
- Johannes, A., et al. In operando x-ray imaging of nanoscale devices: Composition, valence, and internal electrical fields. Science Advances. 3, 1-7 (2017).
- Hieslmair, H., Istratov, A. A., Sachdeva, R., Weber, E. R. New Synchrotron-Radiation Based Technique to Study Localized Defects in Silicon: 'EBIC' with X-Ray Excitation. 10th Workshop on Crystalline Silicon Solar Cell Materials and Processes. , 162-165 (2000).
- Vyvenko, O., et al. X-ray beam induced current - A synchrotron radiation based technique for the in situ analysis of recombination properties and chemical nature of metal clusters in silicon. Journal of Applied Physics. 91, 3614-3617 (2002).
- Stuckelberger, M. E., et al. X-Ray Beam Induced Voltage: A Novel Technique for Electrical Nanocharacterization of Solar Cells. 2017 IEEE 44th Photovoltaic Specialist Conference, PVSC 2017. , (2017).
- Stuckelberger, M. E., et al. How does CIGS performance depend on temperature at the microscale? IEEE Journal of Photovoltaics. 8, 278-287 (2018).
- Stuckelberger, M. E., et al. Challenges and Opportunities with Highly Brilliant X-ray Sources for multi-Modal in-Situ and Operando Characterization of Solar Cells. Microscopy and Microanalysis. 24, 434-435 (2018).
- Zurich Instruments. Principles of Lock-in Detection. , 1-10 (2016).
- Kitchin, C., Counts, L. RMS To DC Conversion Application Guide. , Analog Devices, Inc. (1986).
- Hubbell, J. H., Seltzer, S. M. X-Ray Mass Attenuation Coefficients - NIST Standard Reference Database 126. , (2004).
- Klein, C. A. Bandgap Dependence and Related Features of Radiation Ionization Energies in Semiconductors. Journal of Applied Physics. 39, 2029-2038 (1967).
- ICE. International Electrotechnical Commission) 60904-3 Ed.2: Photovoltaic devices - Part 3: Measurement principles for terrestrial photovoltaic (PV) solar devices with reference spectral irradiance data. , (2006).
- Keithley. Keithley 487/86 Pico-ammeter instruction manual. , (2000).
- ThinkSRS. MODEL SR570 Low-Noise Current Preamplifier. , (2015).
- Scofield, J. H. Frequency-domain description of a lock-in amplifier. American Journal of Physics. 62, 129-133 (1994).
- Poon, T. C. Heterodyning. Encyclopedia of Modern Optics II. 1, Elsevier Ltd. 373 (2005).
- Zurich Instruments. UHF User Manual. , (2018).
- Witte, W., et al. Gallium gradients in Cu(In,Ga)Se2 thin-film solar cells. Progress in Photovoltaics: Research and Applications. 23, 717-733 (2015).
- Fish, P. J. Electronic Noise and Low Noise Design. , The Macmillan Press LTD. (1993).
- Keithley A Tektronix Company. Precision DC Current, Voltage and Resistance Measurements. Low Level Measurements Handbook - 7 th Edition. , (2013).
- Letzter, S., Webster, N. Noise in amplifiers. IEEE Spectrum. 7, 67-75 (1970).
- Meade, M. L. Lock-in amplifiers: principles and applications. , (2013).
- Cazaux, J. A physical approach to the radiation damage mechanisms induced by X-rays in X-ray microscopy and related techniques. Journal of Microscopy. 188, 106-124 (1997).
- Polvino, S. M., et al. Synchrotron microbeam x-ray radiation damage in semiconductor layers. Applied Physics Letters. 92, 6-9 (2008).
- Martínez-Criado, G., et al. Spatially resolved X-ray excited optical luminescence. Nuclear Instruments and Methods in Physics Research B. 284, 36-39 (2012).
- Taylor, R. P., Finch, A. A., Mosselmans, J. F. W., Quinn, P. D. The development of a XEOL and TR XEOL detection system for the I18 microfocus beamline Diamond light source. Journal of Luminescence. 134, 49-58 (2013).
- Cavalcoli, D., Cavallini, A. Evaluation of diffusion length at different excess carrier concentrations. Materials Science and Engineering. B24, 98-100 (1994).
- Micard, G., Hahn, G., Terheiden, B. Injection in light beam induced current systems An analytical model. Physica Status Solidi a. 213, 1329-1339 (2016).
- Marcelot, O., Magnan, P. From EBIC images to qualitative minority carrier diffusion length maps. Ultramicroscopy. , 23-27 (2019).
- Wallentin, J., et al. Hard X-ray detection using a single 100 nm diameter nanowire. Nano Letters. 14, 7071-7076 (2014).
Tags
X-ray Beam Induced Current Multi-modal X-ray Microscopy Solar Cells Electronic Devices Photovoltaic Cells X-ray Detectors Local Device Performance Electron Beam-induced Current Laser Beam Induced Current Encapsulated Solar Cells Charge Collection Efficiency Semi-conductor Devices Nano Wires Sample Holder Kinematic Base Printed Circuit BoardErratum
Formal Correction: Erratum: X-ray Beam Induced Current Measurements for Multi-Modal X-ray Microscopy of Solar Cells
Posted by JoVE Editors on 07/29/2020.
Citeable Link.
An erratum was issued for: X-ray Beam Induced Current Measurements for Multi-Modal X-ray Microscopy of Solar Cells. An equation was updated.
Equation 9 was updated from:
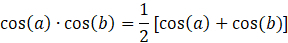
to:
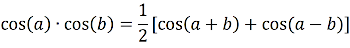



 in addition to
in addition to  (Hz), to convert the count rate back to a current.
(Hz), to convert the count rate back to a current.
 (V/A) at the PA, where the
(V/A) at the PA, where the  signal (measured in ampere) is amplified and converted to a voltage.
signal (measured in ampere) is amplified and converted to a voltage. (V/V) at the LIA.
(V/V) at the LIA. (V) of the V2F converter that is projected onto the frequency range
(V) of the V2F converter that is projected onto the frequency range  (Hz).
(Hz). in the following equation to get the XBIC values in ampere from the frequency values sorted by the DAQ:
in the following equation to get the XBIC values in ampere from the frequency values sorted by the DAQ: with
with  ,
, is a factor which depends on the waveform of the modulation32.
is a factor which depends on the waveform of the modulation32.
 ; and for a square wave,
; and for a square wave,  . Typical values for the measurement of thin-film solar cells at hard X-ray nanoprobes are:
. Typical values for the measurement of thin-film solar cells at hard X-ray nanoprobes are:  ,
,  ,
,  ,
,  .
. for topological variations, use28:
for topological variations, use28: ,
, being the X-ray attenuation coefficient33 and
being the X-ray attenuation coefficient33 and  the mass density for the absorber element
the mass density for the absorber element  which can be measured through simultaneous XRF measurements17.
which can be measured through simultaneous XRF measurements17. , use23:
, use23: ,
, and
and  are the generation and collection rate of electron-hole pairs,
are the generation and collection rate of electron-hole pairs,  is the rate of incident photons,
is the rate of incident photons,  is the elementary charge, and
is the elementary charge, and  is a material constant.
is a material constant. ,
, is the energy deposited in the absorber layer of the DUT per incident X-ray photon,
is the energy deposited in the absorber layer of the DUT per incident X-ray photon,  is the bandgap of the absorber material, and
is the bandgap of the absorber material, and  is a constant.
is a constant. .
. , from the XBIC signal, use:
, from the XBIC signal, use: ,
, is the X-ray beam cross-section, and
is the X-ray beam cross-section, and  is the short-circuit current density under standard measurement conditions35.
is the short-circuit current density under standard measurement conditions35.