קביעת חוקי התעריפים וסדר התגובה
195,721 Views
Overview
מקור: המעבדה של ד”ר ניל אברמס — מכללת SUNY למדעי הסביבה ויערנות
לכל התגובות הכימיות יש שיעור מסוים המגדיר את ההתקדמות של מגיבים הולכים למוצרים. שיעור זה יכול להיות מושפע טמפרטורה, ריכוז, ואת המאפיינים הפיזיים של המגיבים. התעריף כולל גם את המתווכים ואת מצבי המעבר שנוצרים אך אינם המגיבים ולא המוצר. חוק התעריפים מגדיר את תפקידו של כל מגיב בתגובה וניתן להשתמש בו כדי לעצב מתמטית את הזמן הנדרש לתגובה כדי להמשיך. הצורה הכללית של משוואת קצב מוצגת להלן:
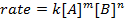
כאשר A ו- B הם ריכוזים של מינים מולקולריים שונים, m ו- n הם סדרי תגובה, ו- k הוא קבוע הקצב. הקצב של כמעט כל תגובה משתנה עם הזמן כאשר המגיבים מתרוקנים, מה שהופך התנגשויות יעילות פחות סביר להתרחש. קבוע הקצב, לעומת זאת, קבוע לכל תגובה בודדת בטמפרטורה נתונה. סדר התגובה ממחיש את מספר המינים המולקולריים המעורבים בתגובה. חשוב מאוד לדעת את חוק התעריפים, כולל קצב קבוע וסדר תגובה, אשר ניתן לקבוע רק באופן ניסיוני. בניסוי זה, נחקור שיטה אחת לקביעת חוק התעריפים ונשתמש בו כדי להבין את התקדמות התגובה הכימית.
Principles
קינטיקה ותרמודינמיקה
כל התגובות הכימיות נשלטות על ידי שני גורמים, קינטיקה ותרמודינמיקה. הגורם התרמודינמי הוא ההבדל באנרגיה חופשית המשתחררת במהלך תגובה כימית. אנרגיה חופשית זו, המכונה ספונטניות, היא ערך מורכב הנובע מהאנטלפיה (חום) והאנטרופיה (הפרעה) בתוך תגובה כימית. קינטיקה מתייחסת לקצב התגובה הכימית וכמה מהר המערכת מגיעה לשיווי משקל. בעוד קינטיקה יכולה להסביר את מהירות התגובה, התרמודינמיקה מניבה מידע על האנרגטיות שלה. במילים פשוטות, התרמודינמיקה מתייחסת ליציבות וקינטיקה מתייחסת לתגובה.
קביעת שיעור
Rate הוא מדידה מבוססת זמן, כלומר הוא משתנה כל הזמן ככל שהתגובה מתקדמת. ניתן לייצג זאת באמצעות חוק שיעור דיפרנציאלי, המבטא את השינוי בריכוז על פני שינוי בזמן. באופן ניסיוני, קשה להשתמש בחוק התעריף הדיפרנציאלי, כך שאנו יכולים להשתמש בחשבון ולייצג את חוק התעריפים כחוק התעריפים המשולב על ידי שילוב חוק התעריף הדיפרנציאלי. חוק התעריף המשולב מייצג את ריכוזי התגובה בתחילת התגובה ובמרווח זמן מוגדר. להלן טבלת סדר, חוק תעריפים וחוק התעריפים המשולבים:
כל סדר מסביר את התלות בריכוז המגיב בשיעור התגובה. לדוגמה, חוק שיעור הזמנה אפסי, rate = k, מציין שהשיעור תלוי רק בקצב הקצב, ולא בריכוז המגיב. זה נפוץ בתגובות קטליטיות שבהן הזרז הוא מוצק ושטח הפנים אינו משתנה במהלך התגובה. חוק שיעור הוראה1 מראה כי השיעור תלוי בריכוז של מגיב אחד, אם כי מגיבים אחרים עשויים להיות נוכחים. חוק שיעור מסדרשני מציין כי השיעור תלוי בריכוז של שני מגיבים בתגובה. מגיבים אלה יכולים להיות זהים, כלומר קצב = k[A]2, או שונה, שיעור = k[A][B]. מכיוון ששני הריכוזים משתנים כל הזמן, קשה למדוד קבועי שיעור מסדר שני במעבדה. ללא קשר לפקודה, שימוש בחוק התעריפים המשולב מפשט את ניתוח הנתונים על-ידי מתן אפשרות להתוויית נתונים והחלת משוואה ליניארית שתתאים לנתונים. מכיוון שרק חוק תעריף משולב אחד יתאים לנתונים, ניתן לזהות באופן מיידי את קצב התגובה ואת סדר התגובה.
ניסוי קינטיקה
קביעת חוק התעריפים מתחילה בהקמת ניסוי קינטיקה לתגובה הכימית. ניסוי קינטיקה נשלט בקפידה כך שהמדידות נעשות במרווחי זמן מתוזמנת על מנת לקבוע את השינוי בריכוז המינים לאורך זמן. מין זה יכול להיות מגיב (הפחתת ריכוז עם הזמן) או מוצר (הגדלת הריכוז עם הזמן). אם מגיבים מרובים מעורבים, חשוב מאוד כי הריכוז של מגיב אחד בלבד משתנה עם הזמן. הגדלת הריכוז של המגיבים האחרים גבוה בהרבה מהמגיב הנחקר גורם לזה להיראות כי הריכוז של מגיב אחד בלבד משתנה במהלך הניסוי.
בניסוי זה, פירוק קטליטי של מי חמצן מעל זרז פלטינה נחקר. מאז הפלטינה היא זרז, רק מין אחד מעורב אשר מתפרק לשני מוצרים על פי התגובה להלן:
2 H2O2(aq) → O2(ז) + 2 H2O(l)
מכיוון שאחד המוצרים, O2, הוא גז, ניתן למדוד את העלייה בלחץ של המערכת לאורך זמן ואת חוק הגז האידיאלי (PV = nRT) המשמש לקשר לחץ מולים. ברגע שזה נעשה עבור כמה ריכוזים שונים של המגיב, ניתן לפתור את סדר התגובה ואת חוק התעריף.
Procedure
1. הכנתח’ 2ו2 דילולים
- מלאי 3% מי חמצן יש ריכוז של 0.882 M. להכין 5 דילולים הנעים בין 0.882 M ל 0.176 M (טבלה 1). הכן פתרונות אלה באופן נפחי, אבל להכין אותם תוסף מאז solute הוא מאוד לדלל וכמויות מים הם תוסף.
- מניחים את הפתרונות באמבט מים בטמפרטורה קבועה או משאירים אותם על הספסל כדי להתפרק בטמפרטורת החדר. טווח טמפרטורות של 20°C (293-298 K) טוב לתגובה זו.
טבלה 1. נעשה שימוש בפתרונות H2O2.
2. הכנת כלי התגובה
- כדי לקבוע את נפח כלי התגובה, מלא מבחנה גדולה למעלה במים והכנס פקק גומי של חור אחד לתוך המבחנה עד הדוק ומים דוחפים את הצדדים ודרך החלק העליון.
- הסר את פקק ויוצקים את המים לתוך גליל מדורג כדי לקבוע את הנפח המדויק של המים. זהו הנפח הכולל של כלי התגובה (מבחנה).
3. מדידת התפתחות החמצן
- החלף את המים עם 50 מ”ל של פתרון מי חמצן הראשון ולהחזיר אותו לתוך אמבט המים. לאחר שיווי משקל, הוסיפו את דיסק התגובה מצופה הפלטינה וחתמו את המערכת עם פקק המחובר לחיישן לחץ גז. דיסקים אלה משמשים בדרך כלל במערכות ניקוי עדשות מגע.
- לאחר חיישן הלחץ מוגדר כדי להשיג נתונים ב 2 נקודות / s, להפעיל את הניסוי עבור 120 s. חיישן לחץ הגז ורנייה, GPS-BTA, מומלץ לניסוי זה.
- בועות יש לראות כמו מי חמצן הוא נרקב גז חמצן ומים. שחררו את הלחץ, נפטרו מהתמיסה, שטפו והחליפו את הפתרון בתמיסת מי חמצן הבאה. חזור על מדידת לחץ הגז עד לבדיקת כל הפתרונות.
4. ניתוח נתונים
- העבר את כל קבצי הנתונים של לחץ לעומת זמן לתוכנית גיליון אלקטרוני.
- קביעת שיעורים ראשוניים – להניח כי הריכוז של מי חמצן לא השתנה הרבה במהלך מסגרת הזמן הקצרה של הניסוי. הנתונים מייצגים את האזור הליניארי הראשוני של ניסוי הקינטיקה.
- קבע שיפוע על-ידי התוויית לחץ לעומת זמן ושימוש בנוסחת שיפוע או רגרסיה ליניארית. שרטט את הלחץ בכל יחידה משותפת.
- השיפוע הוא הקצב ההתחלתי ביחידות לחץO2/s.
- קביעת סדר תגובה
- מכיוון שלחץ של O2 מפותח הוא פרופורציונלי ישירות לשומות של H 2 O2מפורק, התוויית ה- ln (שיעור התחלתי)לעומת ln[H2O2]0 מניבה שיפוע שווה ערך לסדר התגובה. הריכוז הראשוני של מי חמצן, [H2O2]0, הוא מה שהיה בשימוש בכל אחד הניסויים.
- המשוואה לחוק התעריפים היא
. לקיחת הלוגריתם הטבעי (ln) של המשוואה מייצרת משוואה ליניארית 
, כאשר m, השיפוע, הוא סדר התגובה.
- המשוואה לחוק התעריפים היא
- מכיוון שלחץ של O2 מפותח הוא פרופורציונלי ישירות לשומות של H 2 O2מפורק, התוויית ה- ln (שיעור התחלתי)לעומת ln[H2O2]0 מניבה שיפוע שווה ערך לסדר התגובה. הריכוז הראשוני של מי חמצן, [H2O2]0, הוא מה שהיה בשימוש בכל אחד הניסויים.
- קביעת קבוע הקצב, k
- עבור כל גירסת ניסיון, המר את התעריף, PO2/s, ליחידות של atm/s אם התעריף נמצא ביחידה אחרת כגון טור/s.
- מכיוון שבועות התפתחו בתמיסה מימית, הפחיתו את לחץ האדים של המים מלחץ המערכת לכל ניסוי. השיעור החדש משקף רק את הלחץ עקב התפתחות החמצן.
- החל את חוק הגז האידיאלי כדי להמיר את התעריף מ- atm/s לשומות/s בכל ניסוי.
- סידור מחדש של PV = nRT ל- n = PV/RT. יחידתה-אס-1 נותרה ללא שינוי. הנפח שווה לנפח המבחנה פחות נפח הפתרון (50 מ”ל).
- השתמש בתגובה הכימית המאוזנת כדי להמיר מפני מולים של חמצן המיוצר מולים של מי חמצן נרקבים בכל ניסוי.
- חלקו את השומות של H2O2 בנפח התמיסה, 0.050 ליטר, כדי להניב את הטוחנת של H2O2 מפורקת לשניה, [H2O2]/s.
- מכיוון שניסוי זה עוקב אחר קינטיקה מסדר ראשון, חלק את הקצב, [H2O2]/s, לפי ריכוז הפתרון המקורי עבור כל ניסוי, [H2O2]0, כדי להניב קבוע קצב, k. פתרון זה עבור קבוע הקצב ישתנה מעט בהתאם לסדר התגובה שנקבעה בעבר.
- ממוצע קבועי הקצב עבור כל ניסוי יחד מאז הטמפרטורה היא קבועה.
לכל התגובות הכימיות יש קצב מסוים, המגדיר באיזו מהירות המגיבים הופכים למוצרים.
תגובות כימיות נשלטות על ידי שני גורמים: קינטיקה ותרמודינמיקה. גורמים תרמודינמיים מסבירים אם תתרחש תגובה או לא, ואם היא סופגת או פולמת אנרגיה במהלך התהליך.
הקינטיקה מתייחסת לקצב התגובה הכימית, וכמה מהר המערכת מגיעה לשיווי משקל. הקינטיקה של תגובה מתוארת על ידי חוק הקצב הקינטי, המגדיר את הקצב בהתבסס על קבוע קצב תגובה, ריכוז הרכיבים וסדר התגובה.
סרטון זה יציג קינטיקה של תגובה באמצעות משוואת חוק התעריפים, וידגים כיצד לקבוע את חוק התעריף לתגובה מסוימת במעבדה.
עבור תגובה כללית, שיעור התגובה שווה לקצב הקבוע כפול ריכוזי המגיבים, כל אחד מהם הועלה לסדר תגובה. קבוע הקצב, k, קבוע לתגובה בטמפרטורה נתונה.
סדרי התגובה אינם תלויים בקדם הסטויצ’יומטרי. במקום זאת הם תלויים במנגנון התגובה, וממחישים כיצד השיעור קשור לריכוז המגיבים. לדוגמה, אם קצב התגובה אינו משתנה כאשר הריכוז של “A” מכפיל, התגובה אינה תלויה בריכוז, והסדר הוא אפס.
אם השיעור מוכפל כאשר הריכוז של מגיב “A” מכפיל, אז התגובה היא סדר ראשון ביחס “A”. אותה התנהגות נכונה לגבי מגיב “B”. הסדר הכולל של תגובה הוא סכום הזמנות התגובה הבודדות עבור כל מגיב.
במהלך תגובה, ריכוז המגיבים משתנה עם הזמן. שים לב שמשוואת הקצב הבסיסית אינה כוללת זמן כמשתנה, ויכולה לקשר רק קצב וריכוז בנקודת זמן ספציפית. עם זאת, הקצב משתנה ככל שהתגובה מתקדמת וככל שהמגיבים מתרוקנים. שימוש בחוק שיעור דיפרנציאלי יכול לקשר את השינוי בריכוז לזמן.
חוק התעריפים לתגובה חייב להיקבע באופן ניסיוני, כאשר תגובה כימית נשלטת בקפידה בטמפרטורה קבועה, וריכוז המגיבים או המוצרים הנמדדים במרווחי זמן ספציפיים. מאחר שמדידות ריכוז נעשות בנקודות זמן נפרדות, קשה לתאם את חוק השיעור הדיפרנציאלי לנתונים ניסיוניים.
שילוב חוק התעריפים הדיפרנציאליים מביא למשוואה פשוטה יותר, הנקראת חוק התעריפים המשולבים. חוק התעריפים המשולב משווה את ריכוזי המגיבים בתחילת התגובה ובזמן שצוין.
משוואת חוק התעריף המשולב משתנה בהתאם לסדר התגובה. משוואות אלה יכולות ללבוש את הצורה הליניארית y=mx+b. לפיכך, חלקת ריכוז לעומת זמן מניבה התוויה ליניארית למשוואת סדר אפס, התוויה של יומן הריכוז הטבעי לעומת הזמן מניבה התוויה ליניארית למשוואת סדר ראשון, וכן הלאה. על ידי התאמת נתונים ניסיוניים למשוואות אלה, ניתן לקבוע בקלות את סדר התגובה. לאחר מכן ניתן לקבוע את קבוע הקצב, k, באמצעות השיפוע של הקו. לבסוף, היחידות של k משתנות בהתאם לסדר התגובה. עבור תגובת סדר אפס, היחידות הן מולים לליטר לשנייה, עבור תגובת הזמנה ראשונה, היחידות הן שניות הפוכות ולתגובת סדר שני היחידות הן ליטר למטרה לשנייה.
כעת, לאחר שהוסברו יסודות חוקי התעריפים הקינטיים, בואו נבחן כיצד לקבוע באופן ניסיוני את חוק התעריפים לפירוק מי חמצן למים וחמצן.
בניסוי זה, פירוק קטליטי של מי חמצן מעל זרז פלטינה נחקר.
ראשית, להכין 5 דילול של מי חמצן, כפי שמוצג בטבלה. במקרה זה, הריכוזים נעים בין 0.882 – 0.176 M, באמצעות פתרון מניה 3% או 0.882 M. אפשר לפתרונות להתכווות לטמפרטורת החדר.
לאחר מכן, להכין את כלי התגובה באמצעות מבחנה. ראשית לקבוע את הנפח על ידי מילוי מבחנה גדולה למעלה עם מים. לאחר מכן, הכנס פקק גומי 1 חור עד שהוא הדוק ומים דוחפים מתוך החור דרך החלק העליון.
הסר את פקק, ויוצקים את המים לתוך גליל מדורג כדי למדוד את הנפח המדויק. זהו הנפח של כלי התגובה.
לאחר מכן, לשפוך 50 מ”ל של פתרון מי חמצן הראשון לתוך המבחנה, ולאחר מכן למקם את הצינור באמבט מים 25 °C.C. לאחר השתוות, הוסיפו דיסק תגובה מצופה פלטינה וחתמו את המערכת באמצעות פקק המחובר לחיישן לחץ גז.
מאז אחד המוצרים הוא גז חמצן, הגברת הלחץ במערכת משמשת למדידת הגידול בחמצן. הגדר את חיישן הלחץ כדי להשיג נתונים במהירות של 2 נקודות לשנייה, ולאחר מכן הפעל את הניסוי במשך 120 s. בועות צריך להיות גלוי כמו מי חמצן מתפרק גז חמצן ומים.
כאשר תקופת התגובה נגמרת, לשחרר את הלחץ ולהיפטר פתרון מי חמצן. לשטוף את הצינור, ולאחר מכן למלא את הצינור עם פתרון מי חמצן הבא. חזור על מדידת לחץ הגז עבור כל הפתרונות.
התווה את נתוני הלחץ לעומת הזמן עבור כל פתרון. הלחץ של חמצן מפותח הוא פרופורציונלי ישירות מולים של חמצן שנוצר על פי חוק הגז האידיאלי. בעקבות התגובה הכימית, ניתן להשתמש במולים של חמצן שנוצר כדי לחשב את המולים של מי חמצן מפורק. ראשית, נניח שריכוז מי חמצן לא השתנה באופן משמעותי במהלך התקופה הקצרה של הניסוי. לפיכך, הנתונים המותווים מייצגים רק את האזור הראשוני של ניסוי הקינטיקה.
קבע את השיפוע של כל ערכת נתונים באמצעות רגרסיה ליניארית. השיפוע שווה לקצב התגובה ההתחלתי ביחידות לחץ של חמצן לשנייה.
לאחר מכן, התוויית היומן הטבעי של קצב התגובה הראשוני לעומת הלוג הטבעי של ריכוז מי חמצן ראשוני. השיפוע שווה לסדר התגובה, m, והוא שווה בערך לאחד. לכן, התגובה היא סדר ראשון.
השיעור עבור כל ניסוי הוא ביחידות של לחץ בטור, לשנייה. כדי לקבוע את קבוע הקצב, המר תחילה את התעריף ליחידות של אטמוספרות לשניה. מכיוון שהבועות התפתחו בתמיסה מימית, הפחיתו את לחץ האדים של המים מלחץ המערכת לכל ניסוי. הקצב החדש משקף את הלחץ רק עקב התפתחות החמצן.
החל את חוק הגז האידיאלי כדי להמיר את התעריף מאטמוספירות כשלעצמו לשומות לשנייה עבור כל ניסוי. פי שניים מולים של חמצן המיוצרים שווים מולים של מי חמצן נרקבים, על פי סטויצ’ומטריה התגובה הכימית. לאחר מכן, השתמש באמצעי האחסון של התגובה כדי להמיר את יחידות התעריף לאונח לשנייה.
קבע את קבועי הקצב עבור כל ניסוי על-ידי חלוקת קצב הטחינה לכל s לפי הריכוז הראשוני. בניסוי זה, קבוע הקצב הממוצע, k, הוא כ 1.48 x 10-4 לשנייה. התגובה היא סדר ראשון, הידוע מן היומן הטבעי – עלילת בול עץ טבעי שהוצג קודם לכן. לכן, ניתן לכתוב את חוק התעריף כפי שמוצג.
עכשיו כשבדקתם איך לקבוע את חוק התעריף לתגובה כימית, בואו נסתכל על אזורים מסוימים שבהם המושג הזה מיושם.
תגובות כימיות משמשות בסינתזה של תרכובות וחומרים המשמשים במגוון רחב של יישומים מדעיים. חשוב להבין את קצב התגובה בשלבי סינתזה אלה, על מנת לשלוט בהתקדמות התגובה.
לדוגמה, הסינתזה של ננו-קריסטלים קדמיום סלניד וננורודים ממשיכה דרך סדרה של תגובות כימיות. לכל תגובה יש שיעור תגובה נפרד משלה, ולכן שלב הסינתזה נשלט בקפידה על סמך מהירות הידע של התגובה; חלקם איטיים וחלקם מהירים מאוד.
חוק קצב התגובה יכול לשמש גם לתיאור ריקבון רדיואקטיבי, ולקבוע את מחצית החיים של חומר רדיואקטיבי. מחצית החיים מתייחסת לכמות הזמן הנדרשת לריכוז החומר לרדת למחצית הריכוז הראשוני שלו.
רדיואקטיביות עוקבת אחר קינטיקה מסדר ראשון, כלומר הזמן הנדרש לחומר רדיואקטיבי כדי להתפורר לרמה בטוחה יכול להיות מאופיין היטב, ומאפשר הובלה ואחסון נאותים של חומר רדיואקטיבי ופסולת רדיואקטיבית.
בדומה לחומרים רדיואקטיביים, לסמים יש גם מחצית חיים והם מתפרקים בגוף. לדוגמה, תרופות מסוימות יש קבועים שיעור גבוה, כלומר הם להתפרק במהירות, ויש לקחת לעתים קרובות. ידע על שיעור השפלה זה מאפשר קביעת המינון המתאים, השימוש ושיטת המסירה.
הרגע צפית בהקדמה של ג’וב לשיעורי תגובה. עכשיו אתה צריך להבין את הסדרים השונים של תגובות כימיות, איך הם מתייחסים לשיעורי תגובה כימית, וכיצד לקבוע את חוק התעריף לתגובה כימית נתונה במעבדה.
תודה שצפיתם!
Results
נתוני התפתחות חמצן ושיעורים התחלתיים
איור 1. לחץ לעומת נתוני זמן עבור כל ניסוי בטמפרטורה קבועה. השיפוע שווה לקצב המיידי של התגובה.
סדר תגובה
- נתונים עבור חמישה ניסויים וגרף עם שיפוע מפורטים להלן (טבלה 2, איור 2). השיפוע של 0.9353 ≈ 1, הוא ערך שלם של סדר התגובה.
טבלה 2. תוצאות 5 H2O2 ניסויים.
איור 2. חלקת יומן טבעית של ריכוז לעומת שיעור. השיפוע שווה ערך לסדר התגובה.
קצב קבוע, k
- חשב את הקצב מול O2/s באמצעות חוק הגז האידיאלי על ידי תחילה הפחתה של לחץ האדים של מים ב 294 K (הטמפרטורה של ניסוי הקינטיקה), 18.7 טור.
- חשב את קבוע הקצב על-ידי חלוקת הקצב, [H2O2]/s לפי הריכוז ההתחלתי של [H2O2]0.
טבלה 3. חישוב קבוע הקצב, k.
- קבוע הקצב הממוצע, 2.25 x 10-4 s-1 מציין שהתגובה היא הזמנה ראשונה המבוססת על היחידות. ניתן לשכתב את חוק התעריף כ: שיעור = 2.25 x 10-4 s-1[H2O2]0
Applications and Summary
בעוד שקביעת משתני חוק שיעור יכולה להיות מעורבת מתמטית, השיטות הן למעשה די פשוטות. כל עוד ניתן למדוד את היעלמותו של מגיב או מראה של מוצר, ניתן להשתמש בחלקות שיעור כדי לחשב את קבוע הקצב. הרחבה של שיטה זו משמשת לעתים קרובות כדי לקבוע את אנרגיית ההפעלה של תגובה, Ea, על ידי מדידת הקצב וחישוב קבוע הקצב במגוון טמפרטורות. שיטה זו כוללת שימוש במשוואת ארניוס, k = Ae(-Ea/RT). שילוב חוק הקצב, כולל סדר תגובה, עם אנרגיית ההפעלה של תגובה מספק פרופיל קינטי מלא למהירות (או איטית) תגובה מתקדמת ומספק מידע מהעולם האמיתי על האופן שבו גורמים כמו טמפרטורה וריכוז יכולים להשפיע על תגובה זו.
קינטיקה כימית מוצאת יישומים בתעשיות ובתחומים מגוונים כמו תרופות, בטיחות גרעינית, תיקון סביבתי, מסנני קרינה. לדוגמה, תרופה מסוימת עשויה להיות קבועה בקצב גדול מאוד, כלומר היא נרקבת מהר מאוד בגוף. הדבר משפיע על שיטת השימוש, המנונים והמסירה. ביחס למדע הגרעין, רדיואקטיביות עוקבת אחר קינטיקה מסדר ראשון, כלומר הזמן הנדרש לחומר גרעיני כדי להירקב לרמה בטוחה מאופיין היטב. מדידות יהיו דומות מאוד לשיטה המוצגת כאן ויכולות להיות מיושמות גם על ריקבון של מזהמים סביבתיים רבים. באופן דומה, מסנני קרינה גם לדעיכה עם פרופילים קינטיים ידועים המאפשרים ליצרנים ליידע את הצרכנים כמה מהר קרם הגנה צריך להיות מיושם כדי לשמור על רמות בטוחות.
References
- Method adapted from Vetter, T. A., Colombo, D. P. Jr. Kinetics of Platinum-Catalyzed Decomposition of Hydrogen Peroxide, J. Chem. Ed. 80 (7), 788-798 (2003).
- David R. Lide, ed. CRC Handbook of Chemistry and Physics. Boca Raton, Florida: CRC Press (2005).
Transcript
All chemical reactions have a specific rate, which defines how quickly the reactants turn into products.
Chemical reactions are governed by two factors: kinetics and thermodynamics. Thermodynamic factors account for whether or not a reaction will occur, and if it absorbs or gives off energy during the process.
Kinetics refers to the rate of a chemical reaction, and how fast the system reaches equilibrium. The kinetics of a reaction is described by the kinetic rate law, which defines the rate based on a reaction rate constant, the concentration of components, and the order of the reaction.
This video will introduce reaction kinetics using the rate law equation, and will demonstrate how to determine the rate law for a certain reaction in the laboratory.
For a general reaction, the reaction rate equals the rate constant times the concentrations of the reactants, each raised to a reaction order. The rate constant, k, is fixed for a reaction at a given temperature.
The reaction orders are independent of the stoichiometric coefficients. Instead they are dependent on the reaction mechanism, and illustrate how the rate is related to the concentration of reactants. For example, if the reaction rate is unchanged when the concentration of “A” doubles, then the reaction does not depend on concentration, and the order is zero.
If the rate doubles when the concentration of reactant “A” doubles, then the reaction is first order with respect to “A.” The same behavior is true for reactant “B”. The overall order of a reaction is the sum of the individual reaction orders for each reactant.
During a reaction, the concentration of reactants changes with time. Note that that the basic rate equation does not include time as a variable, and can only relate rate and concentration at a specific time point. However, the rate changes as the reaction proceeds and as reactants are depleted. Using a differential rate law can relate the change in concentration to time.
The rate law for a reaction must be determined experimentally, where a chemical reaction is carefully controlled at a constant temperature, and the concentration of the reactants or products measured at specific time intervals. Since concentration measurements are made at discrete time points, the differential rate law is difficult to correlate to experimental data.
Integrating the differential rate law results in a simpler equation, called the integrated rate law. The integrated rate law compares the reactant concentrations at the start of the reaction and at a specified time.
The integrated rate law equation varies depending on the order of the reaction. These equations can take the linear form y=mx+b. Thus, a plot of concentration vs time yields a linear plot for a zero order equation, a plot of the natural log of concentration vs time yields a linear plot for a first order equation, and so on. By fitting experimental data to these equations, the order of a reaction can be easily determined. The rate constant, k, can then be determined using the slope of the line. Finally, the units of k vary depending on the order of the reaction. For a zero order reaction, the units are moles per liter per second, for a first order reaction, the units are inverse seconds and for a second order reaction the units are liter per mole per second.
Now that the basics of kinetic rate laws have been explained, lets take a look at how to experimentally determine the rate law for the decomposition of hydrogen peroxide to water and oxygen.
In this experiment, the catalytic decomposition of hydrogen peroxide over a platinum catalyst is explored.
First, prepare 5 dilutions of hydrogen peroxide, as shown in the table. In this case, concentrations range from 0.882 – 0.176 M, using a 3% or 0.882 M stock solution. Allow the solutions to equilibrate to room temperature.
Next, prepare the reaction vessel using a test tube. First determine the volume by filling a large test tube to the top with water. Then, insert a 1-hole rubber stopper until it is tight and water pushes out of the hole through the top.
Remove the stopper, and pour the water into a graduated cylinder to measure the exact volume. This is the volume of the reaction vessel.
Next, pour 50 mL of the first hydrogen peroxide solution into the test tube, and then place the tube in the 25 °C water bath. Once equilibrated, add a platinum coated reaction disc, and seal the system with a stopper connected to a gas pressure sensor.
Since one of the products is oxygen gas, the increase of pressure in the system is used to measure the increase in oxygen. Set up the pressure sensor to acquire data at 2 points per s, then run the experiment for 120 s. Bubbles should be visible as the peroxide decomposes to oxygen gas and water.
When the reaction period is over, release the pressure and dispose of the peroxide solution. Rinse the tube, then fill the tube with the next hydrogen peroxide solution. Repeat the gas pressure measurement for all solutions.
Plot the pressure versus time data for each solution. The pressure of evolved oxygen is directly proportional to the moles of oxygen formed according to the ideal gas law. Following the chemical reaction, the moles of oxygen formed can be used to calculate the moles of decomposed hydrogen peroxide. First, assume that the concentration of hydrogen peroxide did not change significantly during the short duration of the experiment. Thus, the plotted data represents only the initial region of the kinetics experiment.
Determine the slope of each data set using a linear regression. The slope is equal to the initial reaction rate in units of pressure of oxygen per second.
Next, plot of the natural log of the initial reaction rate vs the natural log of initial peroxide concentration. The slope is equal to the reaction order, m, and is approximately equal to one. Therefore, the reaction is first order.
The rate for each trial is in units of pressure in Torr, per second. To determine the rate constant, first convert the rate to units of atmospheres per second. Because the bubbles evolved in the aqueous solution, subtract the vapor pressure of water from the system pressure for each trial. The new rate then only reflects the pressure due to oxygen evolution.
Apply the ideal gas law to convert the rate from atmospheres per se to moles per s for each trial. Two times the moles of oxygen produced are equal to the moles of hydrogen peroxide decomposed, according to the chemical reaction stoichiometry. Then, use the reaction volume to convert the units of the rate to molarity per second.
Determine the rate constants for each trial by dividing the rate in molarity per s by the initial concentration. In this experiment, the average rate constant, k, is approximately 1.48 x 10-4 per s. The reaction is first order, known from the natural log – natural log plot shown earlier. Therefore, the rate law can be written as shown.
Now that you’ve looked at how to determine the rate law for a chemical reaction, lets look at some areas where this concept is applied.
Chemical reactions are used in the synthesis of compounds and materials used in a wide range of scientific applications. It is important to understand the reaction rate in these synthesis steps, in order to control the progress of a reaction.
For example, the synthesis of cadmium selenide nanocrystals and nanorods proceeds through a series of chemical reactions. Each reaction has its own discrete reaction rate, and therefore synthesis step is carefully controlled based on the knowledge speed of the reaction; some slow and some very quick.
The reaction rate law can also be used to describe radioactive decay, and determine the half-life of radioactive material. Half-life refers to the amount of time required for the concentration of a material to fall to half of its initial concentration.
Radioactivity follows first order kinetics, meaning that the time required for radioactive material to decay to a safe level can be very well characterized, enabling proper transport and storage of radioactive material and radioactive waste.
Similar to radioactive materials, drugs also have a half-life and degrade in the body. For example, some drugs have high rate constants, meaning that they degrade quickly, and must be taken frequently. Knowledge of this degradation rate enables the determination of the appropriate dosage, usage and delivery method.
You’ve just watched JoVE’s introduction to reaction rates. You should now understand the different orders of chemical reactions, how they relate to chemical reaction rates, and how to determine the rate law for a given chemical reaction in the laboratory.
Thanks for watching!
Common Lab Glassware and Uses
General Chemistry
653.7K Views
Solutions and Concentrations
General Chemistry
273.1K Views
Determining the Density of a Solid and Liquid
General Chemistry
554.8K Views
Determining the Mass Percent Composition in an Aqueous Solution
General Chemistry
383.1K Views
Determining the Empirical Formula
General Chemistry
180.0K Views
Determining the Solubility Rules of Ionic Compounds
General Chemistry
141.1K Views
Using a pH Meter
General Chemistry
344.3K Views
Introduction to Titration
General Chemistry
423.4K Views
Ideal Gas Law
General Chemistry
78.2K Views
Spectrophotometric Determination of an Equilibrium Constant
General Chemistry
158.3K Views
Le Châtelier's Principle
General Chemistry
264.0K Views
Freezing-Point Depression to Determine an Unknown Compound
General Chemistry
160.4K Views
Determining Rate Laws and the Order of Reaction
General Chemistry
195.7K Views
Using Differential Scanning Calorimetry to Measure Changes in Enthalpy
General Chemistry
44.4K Views
Coordination Chemistry Complexes
General Chemistry
91.2K Views