Overview
Source: Ricardo Mejia-Alvarez, Hussam Hikmat Jabbar and Mahmoud N. Abdullatif, Department of Mechanical Engineering, Michigan State University, East Lansing, MI
Owing to the non-linear nature of its governing laws, fluid motion induces complicated flow patterns. Understanding the nature of these patterns has been the subject of intense scrutiny for centuries. Although personal computers and supercomputers are extensively used to deduce fluid flow patterns, their capabilities are still insufficient to determine the exact flow behavior for complex geometries or highly inertial flows (e.g. when momentum dominates over viscous resistance). With this in mind, a multitude of experimental techniques to make flow patterns evident have been developed that can reach flow regimes and geometries inaccessible to theoretical and computational tools.
This demonstration will investigate fluid flow around a bluff body. A bluff body is an object that, due to its shape, causes separated flow over most of its surface. This is in contrast to a streamlined body, like an airfoil, which is aligned in the stream and causes less flow separation. The purpose of this study is to use hydrogen bubbles as a method of visualizing flow patterns. The hydrogen bubbles are produced via electrolysis using a DC power source by submerging its electrodes in the water. Hydrogen bubbles are formed in the negative electrode, which needs to be a very fine wire to ensure that the bubbles remain small and track fluid motion more effectively. This method is suitable for steady and unsteady laminar flows, and is based on the basic flow lines that describe the nature of the flow around objects. [1-3]
This paper focuses on describing the implementation of the technique, including details about the equipment and its installation. Then, the technique is used to demonstrate the use of two of the basics flow lines to characterize the flow around a circular cylinder. These flow lines are used to estimate some important flow parameters like flow velocity and the Reynolds number, and to determine flow patterns.
Principles
In this configuration, we will consider a uniform steady flow of water with velocity  (dubbed free-stream velocity) approaching a circular cylinder (Figure 1). Depending on flow conditions as characterized by the Reynolds number, this flow might become unstable and give rise to vortex-shedding. Vortex shedding is typical in flow past bluff bodies which, as opposed to streamlined bodies, exhibit boundary layer separation over a substantial portion of their surface. This boundary layer separation leads to the formation of vortices behind the body that could eventually detach periodically into the wake. When periodical detachment takes place, the vortices generate alternating areas of low pressure behind the body that could become resonant loads if the shedding frequency coincides with the natural frequency of the body. This vortex shedding process is called the "Von Kármàn vortex street" (Figure 2). This repeating pattern of swirling vortices is caused by unsteady flow separation around the bluff body and occurs at certain ranges of Reynolds number. Avoiding this scenario is of significant importance in designing engineering structures such as smoke stacks and bridge pillars since it could result in catastrophic failure.
(dubbed free-stream velocity) approaching a circular cylinder (Figure 1). Depending on flow conditions as characterized by the Reynolds number, this flow might become unstable and give rise to vortex-shedding. Vortex shedding is typical in flow past bluff bodies which, as opposed to streamlined bodies, exhibit boundary layer separation over a substantial portion of their surface. This boundary layer separation leads to the formation of vortices behind the body that could eventually detach periodically into the wake. When periodical detachment takes place, the vortices generate alternating areas of low pressure behind the body that could become resonant loads if the shedding frequency coincides with the natural frequency of the body. This vortex shedding process is called the "Von Kármàn vortex street" (Figure 2). This repeating pattern of swirling vortices is caused by unsteady flow separation around the bluff body and occurs at certain ranges of Reynolds number. Avoiding this scenario is of significant importance in designing engineering structures such as smoke stacks and bridge pillars since it could result in catastrophic failure.

Figure 1. Flow past a circular cylinder. Schematic of basic configuration. A homogeneous stream with velocity  approaches a straight cylinder of diameter
approaches a straight cylinder of diameter  whose axis of symmetry is perpendicular to the approaching velocity.
whose axis of symmetry is perpendicular to the approaching velocity.
The Reynolds number is a dimensionless parameter defined as the ratio of inertial forces to viscous forces:
 (1)
(1)
Where  is the kinematic viscosity of the fluid,
is the kinematic viscosity of the fluid,  a characteristic velocity (
a characteristic velocity ( in the present case), and
in the present case), and  the cylinder diameter. The Reynolds number is arguably the most important parameter in the characterization of fluid flow and will be used throughout the present experiment as the metric for the emergence of the Von Kármàn vortex street. In particular, when the Reynolds number is around 5, the flow exhibits two stable counter-rotating vortices behind the cylinder. As the Reynolds number increases, these two vortices elongate in the direction of the flow. When the Reynolds number reaches a value of approximately 37, the wake becomes unstable and begins to oscillate sinusoidally as a result of an imbalance between pressure and momentum. A further increase in Reynolds number up to 47 causes the two counter-rotating vortices to detach from the cylinder in an alternating sequence that follows the sinusoidal wake oscillation [4,5,6].
the cylinder diameter. The Reynolds number is arguably the most important parameter in the characterization of fluid flow and will be used throughout the present experiment as the metric for the emergence of the Von Kármàn vortex street. In particular, when the Reynolds number is around 5, the flow exhibits two stable counter-rotating vortices behind the cylinder. As the Reynolds number increases, these two vortices elongate in the direction of the flow. When the Reynolds number reaches a value of approximately 37, the wake becomes unstable and begins to oscillate sinusoidally as a result of an imbalance between pressure and momentum. A further increase in Reynolds number up to 47 causes the two counter-rotating vortices to detach from the cylinder in an alternating sequence that follows the sinusoidal wake oscillation [4,5,6].
The frequency with which vortices are shed off the cylinder is not constant; it varies with the value of the Reynolds number. Shedding frequency is characterized by the Strouhal number, which is the other dimensionless parameter of relevance in this particular fluid flow configuration:
 (2)
(2)
Here, ![]() is the vortex shedding frequency and the length and velocity scales are the same as for the Reynolds number. Vortex shedding frequency can then be characterized by the Strouhal number as a linear function of the inverse square root of the Reynolds number [7]:
is the vortex shedding frequency and the length and velocity scales are the same as for the Reynolds number. Vortex shedding frequency can then be characterized by the Strouhal number as a linear function of the inverse square root of the Reynolds number [7]:
 (3)
(3)
This function is not always monotonic, it exhibits further transitions as a result of secondary instabilities owed to the non-linearity of fluid flow. As a result, the coefficients  and
and  would change according to the Reynolds number range. Table 1 shows the values of these coefficients for the flow regimes that have been well characterized in the literature [7].
would change according to the Reynolds number range. Table 1 shows the values of these coefficients for the flow regimes that have been well characterized in the literature [7].
During the present experiments, we will use flow lines to study external flow around a circular cylinder. These flow lines are defined as follows:
• Pathline: path that a fluid particle follows as it moves with the flow.
• Streakline: continuous locus of all the fluid particles whose motion originated at the same spatial location.
• Timeline: set of fluid particles that were tagged at the same instant of time while forming a continuous locus.
• Streamline: continuous line that is everywhere tangent to the velocity field at an instant in time.
The first three lines are relatively easy to generate experimentally, while streamlines are merely a mathematical concept that in general have to be produced by post-processing an instantaneous capture of the velocity field. While this is always true, the analysis simplifies significantly in steady flows because pathlines, streaklines, and streamlines coincide with each other. Conversely, these lines do not generally coincide with each other in unsteady flows. The implementation of this technique is generally simple and requires only low-cost equipment, as opposed to more sophisticated and expensive techniques such as Particle Image Velocimetry [1], Particle Tracking Velocimetry [8,9], and Molecular Tagging Velocimetry [10].

Figure 2. Representative results. (A) continuous sheet of hydrogen bubbles that shows streaklines as a result of upstream disturbances. The shadow cast by the rod is used to determine the conversion from machine to real units. A vortex shedding cycle is also illustrated to help determine shedding frequency appropriately. (B) timelines generated with hydrogen bubbles. Since timeline frequency is well-defined, they can be used to measure flow velocity accurately; counting the timelines enclosed in the red lines will be used for this estimation. Please click here to view a larger version of this figure.
Table 1. Values of the coefficients  and
and  for different Reynolds number intervals (from [8]).
for different Reynolds number intervals (from [8]).

Subscription Required. Please recommend JoVE to your librarian.
Procedure
1. To produce a continuous sheet of bubbles:
- Set the equipment according to the electrical diagram shown in Figure 3.
- Fix the positive electrode in the water at the downstream end of the test section (see Figure 4 for reference).
- Fix the negative electrode upstream and near the point of interest to release the bubbles into the stream before the flow reaches the object of study (see Figure 4 for reference). The water completes the circuit between the two electrodes.
- Turn on the flow facility
- Set the dial of the frequency controller to position 2. This will establish a flow rate of about 9x10-4 m3/s.
- Turn on the DC power supply and increase the voltage up to about 25 V, the current will set itself around 190 mA.
- Set the wave form in the signal generator to Square Wave (symbol:
 ). This generates a 0 V - 5 V square signal that activates the solid-state relay (closing the circuit) in its high position and opens it in the low position
). This generates a 0 V - 5 V square signal that activates the solid-state relay (closing the circuit) in its high position and opens it in the low position - For this particular case, the frequency of the square wave is not important. It just needs to be non-zero.
- Maximize the DC offset (+5 V) in the signal generator. With this setting, the circuit is always closed and the system generates bubbles continuously.

Figure 3. Connections diagram.

Figure 4. Test section. Flow goes from left to right. The negative electrode generates a layer of hydrogen bubbles that are swept away with the flow. The positive electrode is set at the downstream end of the test section to avoid its disturbances. Please click here to view a larger version of this figure.
2. To produce timelines:
- Turn on the flow facility
- Set the dial of the frequency controller to position 2. This will establish a flow rate of about 9x10-4 m3/s.
- Turn on the DC power supply and increase the voltage up to about 25 V, the current will set itself around 190 mA.
- Set the wave form in the signal generator to Square Wave (symbol:
 ). This generates a 0 V - 5 V square signal that activates the solid-state relay (closing the circuit) in its high position and deactivates it (opening the circuit) in the low position
). This generates a 0 V - 5 V square signal that activates the solid-state relay (closing the circuit) in its high position and deactivates it (opening the circuit) in the low position - Set the DC offset in the signal generator at +1 V.
- Set the frequency of the square wave in the signal generator at 10 Hz.
- Set the symmetry of the square wave slightly negative (-2) to increase the space between timelines while conserving the right frequency.
3. To use flow lines to study Von Kármàn vortex streets:
- Measure the diameter of the rod,
 , using a caliper. Use S.I. units for this measurement (m).
, using a caliper. Use S.I. units for this measurement (m). - Fix a cylindrical rod downstream of the negative electrode.
- Cast the light of the high-intensity discharge lamp on the layer of hydrogen bubbles. Make sure the light is not directly behind of the line of view to prevent oversaturation of the imaging system
- Align the visualization system with the rod; in a way that only the circular tip is visible in front of the camera.
- Add a mark in the visualization window and downstream of the rod to use it as the reference to count vortex-shed cycles per unit time.
4. Data analysis for flow past a circular cylinder:
- Determination of the conversion factor from machine units to real space units:
- Measure the width of the shadow cast by the rod on the bubble sheet (see figure 2(A) for reference). Take this measurement right at the rod to avoid distortion with distance. This is the diameter of the rod in machine units,
 (points or pixels, depending on format)
(points or pixels, depending on format) - Use the following equation to determine the conversion factor from machine units to real world units:

- Measure the width of the shadow cast by the rod on the bubble sheet (see figure 2(A) for reference). Take this measurement right at the rod to avoid distortion with distance. This is the diameter of the rod in machine units,
- Determination of flow velocity:
- Choose a group of undistorted timelines upstream of the bluff body.
- Measure the distance between the first and last timeline in machine units,
 (points or pixels).
(points or pixels). - Count the number of timelines in the group,
 .
. - Take note of the frequency of the square wave signal as produced by the signal generator,
 .
. - Determine the approaching flow velocity from the following equation:

- Determination of the Reynolds number:
- Find the kinematic viscosity of the working fluid (e.g. water
 m2/s).
m2/s). - Calculate the Reynolds number using equation (1). For that, considering the diameter of the rod (
 ) measured in step 3.1, the approaching velocity (
) measured in step 3.1, the approaching velocity ( ) determined with equation (5), and the kinematic viscosity determined in step 4.3.1
) determined with equation (5), and the kinematic viscosity determined in step 4.3.1
- Find the kinematic viscosity of the working fluid (e.g. water
- Determination of the Strouhal number: the vortices in the wake of the rod are moving at a different velocity as the timelines in the free stream. Hence, the frequency of vortex shedding needs to be estimated independently.
- Define a fixed reference downstream of the rod. This reference could be a fine string attached to the exterior of the tunnel or a digital line added to a video of the flow process.
- Count the number of vortex shedding cycles,
 , crossing the reference during a defined period of time
, crossing the reference during a defined period of time  . A vortex shedding cycle is illustrated in Figure 2(A).
. A vortex shedding cycle is illustrated in Figure 2(A). - Calculate the shedding frequency from the following equation:

- Use the results from equations (5) and (6) in equation (2) to calculate the Strouhal number.
Due to the nonlinear nature of its governing laws, fluid motion induces complicated flow patterns. These flow patterns are influenced by many factors, one of which is flow past an obstacle such as a bluff body. A bluff body is an object that, due to its shape, causes separated flow over most of its surface. Depending on the flow conditions, this flow may become unstable, giving rise to oscillating flow patterns in the wake called vortex shedding. This video will introduce the basics of flow separation and vortex shedding caused by a bluff body and demonstrate a technique used to visualize the resulting flow patterns.
First, let's consider the uniform steady flow of water with velocity U infinity called the free stream velocity approaching a circular cylinder. Boundary layer separation on the object's surface leads to the formation of vortices around the body that eventually detach into the wake. When periodic detachment takes place, the vortices generate alternating areas of low pressure behind the body. This process is called the Von Karman vortex street. This repeating pattern occurs at certain ranges of Reynolds number, a dimensionless parameter defined as the ratio of inertial forces to viscous forces. Here, nu is the kinematic viscosity of the fluid, V is the characteristic velocity or U infinity in this case, and D is the cylinder diameter. For example, in the setup in the following demonstration, when the Reynolds number is around five, the flow exhibits two stable counter-rotating vortices behind the cylinder. As the Reynolds number increases, these vortices elongate in the direction of the flow. When the Reynolds number reaches approximately 37, the wake becomes unstable and oscillates sinusoidally as a result of an imbalance between pressure and momentum. The frequency in which vortices are shed off the cylinder is not constant, rather it varies with the value of the Reynolds number. This shedding frequency is characterized by the Strouhal number, which is another dimensionless parameter. The Strouhal number is defined as shown where f is the vortex shedding frequency. Experimental analysis of flow patterns uses four types of flow lines. A path line is the path that a given fluid particle follows as it moves with the flow. A streak line is the continuous locus of all fluid particles whose motion originated from the same location. A streamline is an imaginary line that is instantaneously and locally tangent to the velocity field. Note that path lines, streak lines, and streamlines coincide with each other under steady flow conditions. In the current flow, this corresponds to regions of the flow upstream from the bluff body or far enough from the influence of its wake. On the other hand, path lines, streak lines, and streamlines differ from each other under unsteady flow conditions. In the current flow, this corresponds basically to the wake of the bluff body. Finally, timelines are the continuous locus of fluid particles that were released to the flow at the same instant in time. In the following experiment, we will use a continuous sheet of tiny hydrogen bubbles to analyze flow patterns using timelines and streak lines. Now, let's take a look at how to set up the flow experiment.
First, assemble the equipment according to the electrical diagram shown. Fix the positive electrode in the water at the downstream end of the test section. Next, fix the negative electrode upstream. This should be near the point where the bubbles are released into the stream before the flow reaches the object of study. Turn on the flow facility. Then set the dial of the frequency controller to position two in order to establish a mean velocity of about 0.04 meters per second. This velocity corresponds to a flow rate of about 50 to the minus fifth cubed meters per second. Now turn on the DC power supply and increase the voltage to about 25 volts with the current around 190 milliamps. On a signal generator, set the output to a square wave with a zero-volt to five-volt square signal that closes the circuit in its high position and opens it in the low position. Maximize the DC offset to five volts so that the circuit is always closed and the system generates bubbles continuously. To produce timelines, change the DC offset in the signal generator to one volt. Then set the frequency of the square wave to 10 Hertz. Timelines will be produced in the flow. Then set the symmetry of the square wave to minus two in order to increase the space between timelines.
First measure the diameter of the rod using a caliper in SI units. Fix the cylindrical rod downstream of the negative electrode. Cast high-intensity light on the layer of hydrogen bubbles, making sure that the light is not directly behind the line of view to prevent over saturation of the imaging system. Align the visualization system with the rod so that only the circular tip is visible in front of the camera. Add a mark in the visualization window and downstream of the rod to use it as the reference point to count vortex shed cycles.
First measure the width of the shadow cast by the rod on the bubble sheet. Take the measurement right at the rod to avoid distortion with distance. Use the rod diameter to determine the conversion factor from machine units to real-world units. Next, choose a group of nearly undistorted timelines away from the bluff body and the influence of its wake. Measure the distance L between the first and last timeline in machine units. Count the number of timelines in the group and note the frequency of the square wave. Determine the approaching flow velocity from the following equation. Now using the kinematic viscosity of water, calculate the Reynolds number. Next, determine the Strouhal number by observing the vortices in the wake of the rod. Note that the vortices move at a different velocity as compared to the timelines in the free stream. Using the fixed string as reference, count the number of vortex shedding cycles, NS, crossing the reference point during a defined period of time. Calculate the shedding frequency. Then use the results to calculate the Strouhal number.
Now that we have gone over the procedure and analysis, let's take a look at the results. The validity of the result can be determined using a relationship between the Reynolds number and the Strouhal number. The coefficients St* and m depend on the Reynolds number range and can be found in the literature. The Reynolds number in this example is 115. Thus, the values of St* and m can be used to calculate the Strouhal number. The calculated value for the Strouhal number is 0.172, which correlates well to the measured value of 0.169. When this experiment was conducted with varying operational parameters, the calculations of the Reynolds and Strouhal numbers correlated well to the mathematical relationship between the two numbers. This shows how well the bubble method can be used to understand flow patterns around a bluff body.
Understanding flow patterns is essential to the design and operation of many types of engineering applications. Pillars of bridges and offshore oil rigs are designed to withstand the turbulence caused by current flow past the structure. Knowing the vortex shedding frequencies at which a given structure will be exposed is critical for its design. In that regard, engineers have to make sure that the natural frequency of the structure is not such that it will resonate with the vortex shedding frequency because this will inevitably lead to catastrophic failure of the structure. It is also essential to study fluid flow around a streamline object such as an air foil or ship hull. By making use of flow lines, engineers can determine parameters such as the angle at which an airplane stalls or even estimate lift characteristics based on flow velocity.
You've just watched Jove's video on visualizing flow lines around a bluff body. You should now understand the basics of fluid flow patterns and the Von Karman vortex street, how to set up an experiment to visualize these flow patterns, and how to study the flow behavior. Thanks for watching.
Subscription Required. Please recommend JoVE to your librarian.
Results
Figure 2 shows two representative results of hydrogen bubble visualization of a Von Kármàn vortex street. Figure 2(A) shows an example of a field of streaklines as evidenced by disturbances in the hydrogen bubble sheet. This image is used to extract the diameter of the rod in machine units. Figure 2(B) shows an example of a field of timelines. This image is used to estimate the approaching fluid velocity. The parameters extracted from this particular experiment are summarized in table 2.
Table 2. Representative results for flow past a circular cylinder.
| Parameter | Value |
| D_o | 0.003 m |
| D_i | 14.528 pts |
| f_s | 2.169 Hz |
| f_tl | 10 Hz |
| L | 130.167 "pts" |
| M | 4842.67 "pts" ∕"m" |
| N_s | 60 |
| N_tl | 7 |
| T | 27.66 s |
| U_∞ | 0.0384 m/s |
| ν | 1.004×[10]^(-6) m2/s |
| Re | 115 |
| St | 0.169 |
Since the Reynolds number is 115 for the present example, the validity of this result can be tested using equation (3) for 
 (7)
(7)
From which we obtain:
 (8)
(8)
After comparing this estimation with our experimental result (see table 2 for reference), we can conclude that our experiment offered a satisfactory result. Figure 5 shows a set of experimental results compared with the predictions of equation (7).

Figure 5. Experimental results. Comparison of current experimental results against predictions of the relation between the Reynolds number and the Strouhal number for flow past a circular cylinder.
Subscription Required. Please recommend JoVE to your librarian.
Applications and Summary
In this study, the usage of hydrogen bubbles was demonstrated to extract qualitative and quantitative information from images of flow around a circular cylinder. The quantitative information extracted from these experiments included the free-stream velocity ( ), vortex-shedding frequency (
), vortex-shedding frequency ( ), Reynolds number (Re), and the Strouhal number (St). In particular, the results for St vs Re exhibited very good agreement with previous studies [3].
), Reynolds number (Re), and the Strouhal number (St). In particular, the results for St vs Re exhibited very good agreement with previous studies [3].
Due to the slow velocity used in the current experiments, perturbations in the bubble sheet produce a streaky bubble layer. These streaks are basically streaklines. As the hydrogen bubble sheet travels downstream, these streaklines thicken and become more irregular. This is the result of turbulence intensity in the free-stream. The effect is attenuated as the velocity of the tunnel is increased since the bubbles leave the test section before presenting a significant dispersion. Streaklines can also be produced at pre-selected locations by coating the wire while leaving small parts of it exposed to water.
The current flow behavior is directly applicable to flow past engineering structures such as the pillars of bridges and offshore oil-rigs, wind turbine towers, or power line poles to name a few. And in fact, this behavior is exhibited by bluff bodies with geometries other than cylindrical such as sky scrapers. Given that vortices generate fluid-structure interactions that make structures oscillate, knowing the vortex shedding frequencies at which a given structure will be exposed is critical for its design. In that regard, the engineer has to make sure that the natural frequency of the structure is not such that it will resonate with the vortex shedding frequency, because this effect will inevitably lead to catastrophic failure of the structure. Using appropriate scaling laws [10] and hydrogen bubbles in a water tunnel, an engineer can simulate the interaction of flow with a structure prior to its construction to make sure that its design is safe or to find out if it needs any modifications.
Besides bluff bodies, hydrogen bubble visualization is a very powerful tool to study flow around streamlined bodies such as airfoils or ship hulls. By making use of flow lines generated with this technique, one can determine parameters such as the angle of attack at which stall takes place, or even estimate lift characteristics based on flow velocity. More importantly, the pattern of distortion of fluid lines will help the engineer to optimize its design.
Visualization with hydrogen bubbles is not restricted to external flows like the above mentioned. This method can also be used to observe the flow through open channels or fully confined flow systems. In the latter case, the walls will need to be transparent to ensure optical access. For example, if one is interested in designing a flow diffuser for sub-sonic flow, hydrogen bubbles can be used to determine geometric and flow conditions for which the diffuser will exhibit flow separation and instability. Based on those observations, the design could be experimentally optimized to ensure its proper functionality.
Subscription Required. Please recommend JoVE to your librarian.
References
- Zöllner, F. Leonardo da Vinci 1452-1519: sketches and drawings, Taschen, 2004.
- White, F. M. Fluid Mechanics, 7th ed., McGraw-Hill, 2009.
- Adrian, Ronald J., and Jerry Westerweel. Particle Image Velocimetry. Cambridge University Press, 2011.
- Gerrard, J. H., The wakes of cylindrical bluff bodies at low Reynolds number, Phil. Trans. Roy. Soc. (London) Ser. A, Vol. 288, No. 1354, pp. 351-382 (1978)
- Coutanceau, M. and Bouard, R., Experimental determination of the viscous flow in the wake of a circular cylinder in uniform translation. Part 1. Steady flow, J. Fluid Mech., Vol. 79, Part 2, pp. 231-256 (1977)
- Kovásznay, L. S. G., Hot-wire investigation of the wake behind cylinders at low Reynolds numbers, Proc. Roy. Soc. (London) Ser. A, Vol. 198, pp. 174-190 (1949)
- Fey, U., M. König, and H. Eckelmann. A new Strouhal-Reynolds-number relationship for the circular cylinder in the range
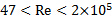 . Physics of Fluids, 10(7):1547, 1998.
. Physics of Fluids, 10(7):1547, 1998. - Maas, H.-G., A. Grün, and D. Papantoniou. Particle Tracking in three dimensional turbulent flows - Part I: Photogrammetric determination of particle coordinates. Experiments in Fluids Vol. 15, pp. 133-146, 1993.
- Malik, N., T. Dracos, and D. Papantoniou Particle Tracking in three dimensional turbulent flows - Part II: Particle tracking. Experiments in Fluids Vol. 15, pp. 279-294, 1993.
- Tropea, C., A.L. Yarin, and J.F. Foss. Springer Handbook of Experimental Fluid Mechanics. Vol. 1. Springer Science & Business Media, 2007.
- Monaghan, J. J., and J. B. Kajtar. Leonardo da Vinci's turbulent tank in two dimensions. European Journal of Mechanics-B/Fluids. 44:1-9, 2014.
- Becker, H.A. Dimensionless parameters: theory and methodology. Wiley, 1976.





 ). This generates a 0 V - 5 V square signal that activates the solid-state relay (closing the circuit) in its high position and opens it in the low position
). This generates a 0 V - 5 V square signal that activates the solid-state relay (closing the circuit) in its high position and opens it in the low position , using a caliper. Use S.I. units for this measurement (m).
, using a caliper. Use S.I. units for this measurement (m). (points or pixels, depending on format)
(points or pixels, depending on format)
 (points or pixels).
(points or pixels). .
. .
.
 m2/s).
m2/s). ) measured in step 3.1, the approaching velocity (
) measured in step 3.1, the approaching velocity ( , crossing the reference during a defined period of time
, crossing the reference during a defined period of time  . A vortex shedding cycle is illustrated in Figure 2(A).
. A vortex shedding cycle is illustrated in Figure 2(A).