14.7: The Small x Assumption
If a reaction has a small equilibrium constant, the equilibrium position favors the reactants. In such reactions, a negligible change in concentration may occur if the initial concentrations of reactants are high and the Kc value is small. In such circumstances, the equilibrium concentration is approximately equal to its initial concentration. This estimation can be used to simplify the equilibrium calculations by assuming that some equilibrium concentrations are equal to the initial concentrations. However, to make this assumption, the change in the concentration of a weak acid or base, i.e., x, must be less than 5% of its initial concentration. If x is more than 5%, then the quadratic formula needs to be used to solve the equilibrium equation.
Calculation of Equilibrium Concentrations Using an Algebra-Simplifying Assumption
What are the concentrations at equilibrium of a 0.15 M solution of HCN?
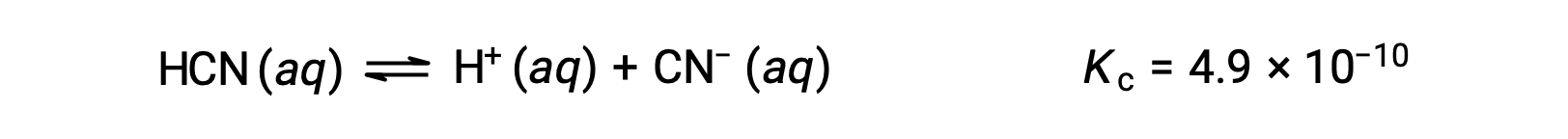
Using x to represent the concentration of each product at equilibrium gives this ICE table.
| HCN (aq) | H+ (aq) | CN− (aq) | |
| Initial Concentration (M) | 0.15 | 0 | 0 |
| Change (M) | −x | +x | +x |
| Equilibrium Concentration (M) | 0.15 − x | x | x |
Substitute the equilibrium concentration terms into the Kc expression
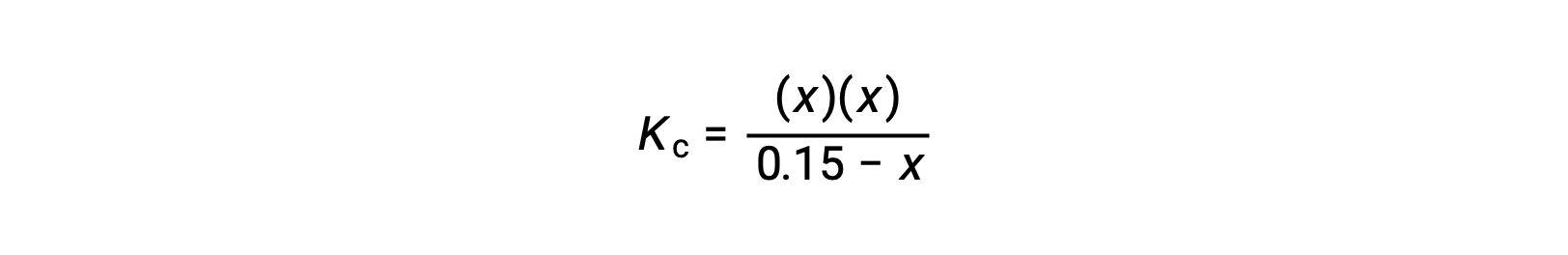
rearrange to the quadratic form and solve for x
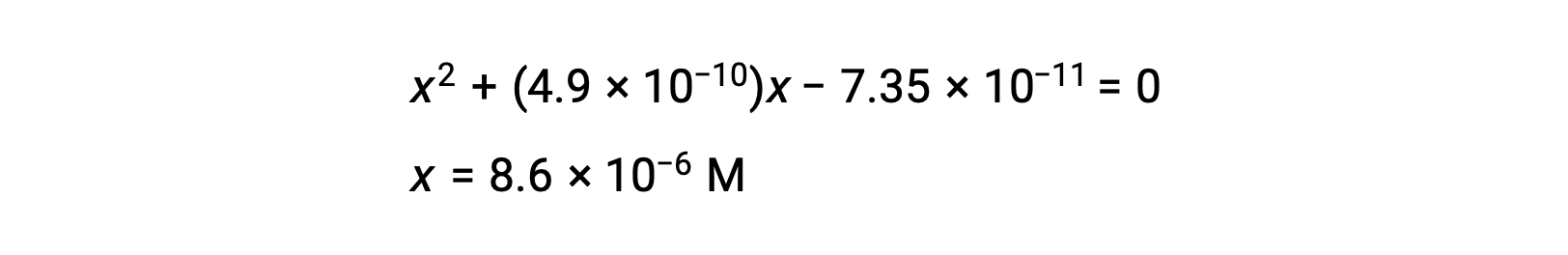
Thus, [H+] = [CN–] = x = 8.6 × 10–6 M and [HCN] = 0.15 – x = 0.15 M.
Note in this case that the change in concentration is significantly less than the initial concentration (a consequence of the small K), and so the initial concentration experiences a negligible change:

This approximation allows for a more expedient mathematical approach to the calculation that avoids the need to solve for the roots of a quadratic equation:
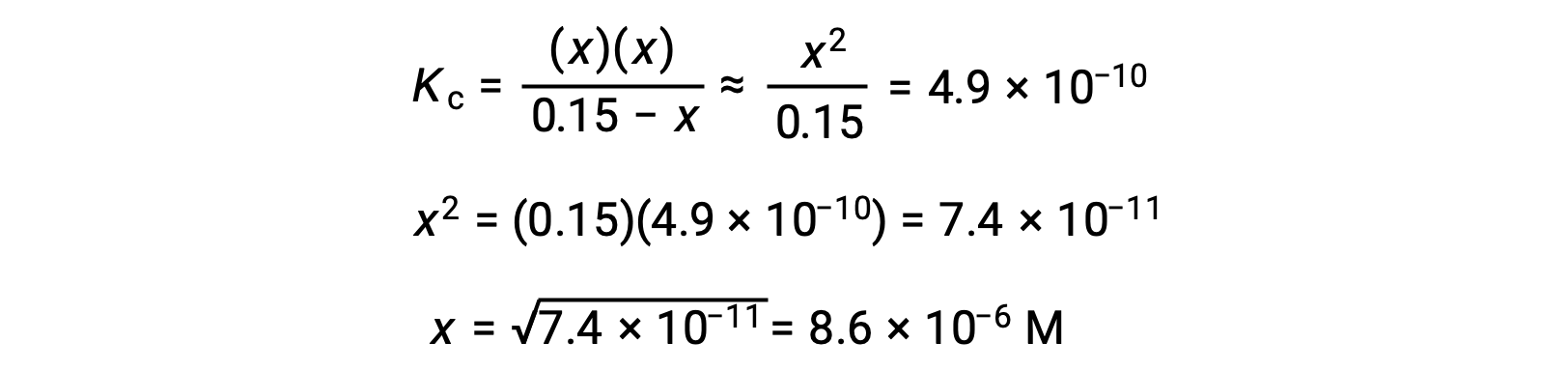
The value of x calculated is, indeed, much less than the initial concentration
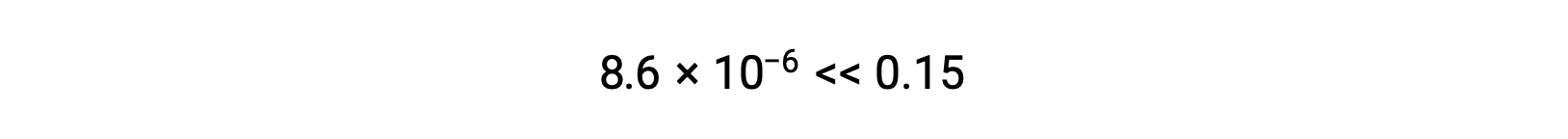
and so the approximation was justified. If this simplified approach were to yield a value for x that did not justify the approximation, the calculation would need to be repeated without making the approximation.
This text has been adapted from Openstax, Chemistry 2e, Section 13.4 Equilibrium Calculations.


