5.3: Applications of the Ideal Gas Law: Molar Mass, Density, and Volume
The volume occupied by one mole of a substance is its molar volume. The ideal gas law, PV = nRT, suggests that the volume of a given quantity of gas and the number of moles in a given volume of gas vary with changes in pressure and temperature. At standard temperature and pressure, or STP (273.15 K and 1 atm), one mole of an ideal gas (regardless of its identity) has a volume of about 22.4 L — this is referred to as the standard molar volume.
For example, one mole each of hydrogen, oxygen, argon, or carbon dioxide occupies 22.4 liters at STP. This implies that 0.5 moles of any gas at STP occupies a volume of 11.2 L, and similarly, 2 moles of any gas at STP occupies a volume of 44.8 L.
The ideal gas law is universal, relating the pressure, volume, number of moles, and temperature of a gas regardless of the chemical identity of the gas:
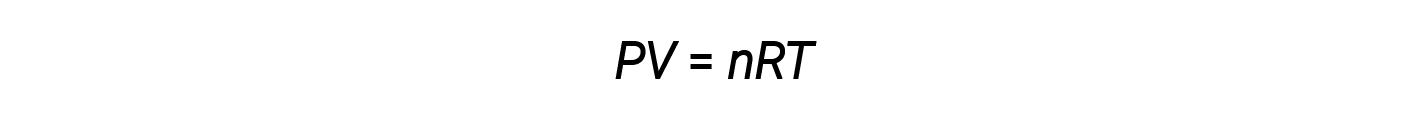
The density d of a gas, on the other hand, is determined by its identity. Density is the ratio of mass over volume. Rearranging the ideal gas equation to isolate V and substituting into the density equation yields:
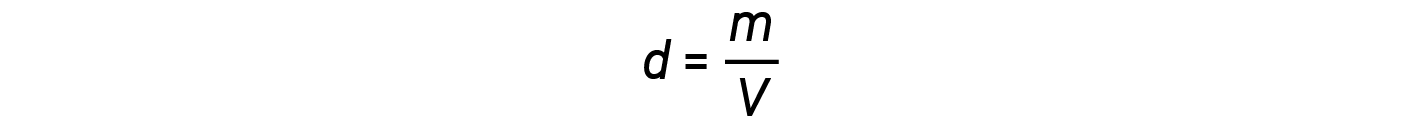
The ratio m/n that is, mass over moles, is the definition of molar mass, M:
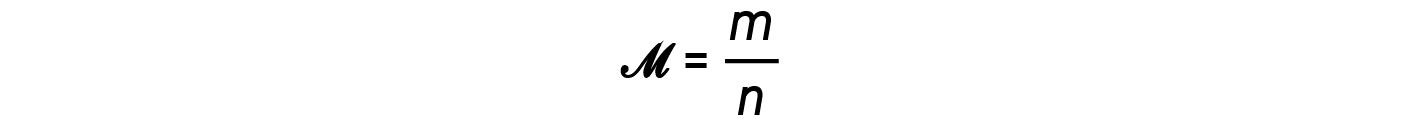
The density equation can then be written as
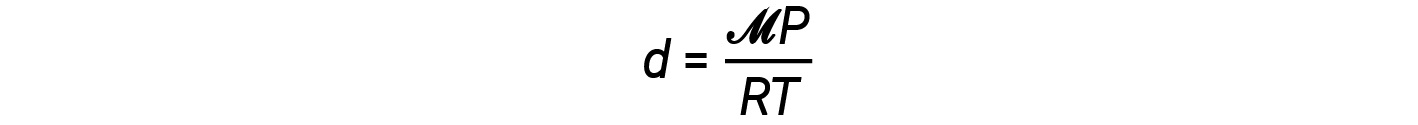
This equation tells us that gas density is directly proportional to the pressure and molar mass, and inversely proportional to the temperature. For example, CO2 (molar mass = 44 g/mol) is heavier than N2 (molar mass = 28 g/mol) or O2 (molar mass = 32 g/mol), and is therefore denser than air. For this reason, CO2 released from a CO2 fire extinguisher blankets a fire, preventing O2 from reaching the combustible material. The phenomenon of the lifting of hot air balloons depends on the relationship that gases of equal molar masses (such as air) have lower densities at higher temperatures, and therefore hot air balloons can float.
This text is adapted from Openstax, Chemistry 2e, Section 9.3: Stoichiometry of Gaseous Substances, Mixtures, and Reactions.


