5.4: Mixtures of Gases: Dalton's Law of Partial Pressures and Mole Fractions
Unless individual gases chemically react with each other, the individual gases in a mixture of gases do not affect each other’s pressure. Each gas in a mixture exerts the same pressure that it would exert if it were present alone in the container. The pressure exerted by each individual gas in a mixture is called its partial pressure.
This means that in a mixture containing three different gases A, B, and C, if PA is the partial pressure of gas A; PB is the partial pressure of gas B; PC is the partial pressure of gas C; then the total pressure is given by equation 1:
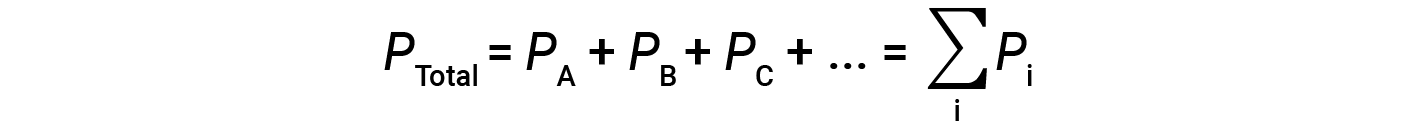
This is Dalton’s law of partial pressures: The total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases.
Let nA, nB, and nC be the number of moles of each of the gases in the mixture. If each gas obeys the ideal-gas equation, the partial pressure can be written as:
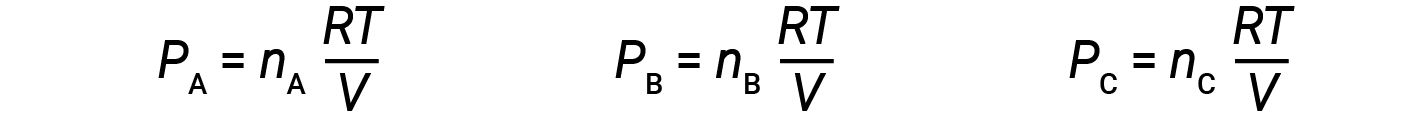
Since all gases are at the same temperature and occupy the same volume, substituting into equation 1 gives:
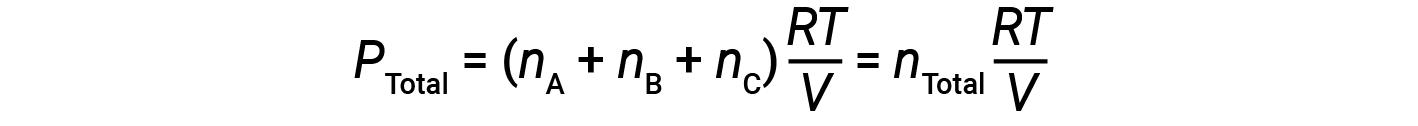
The equation indicates that at constant temperature and constant volume, the total pressure of a gas sample is determined by the total number of moles of gas present.
For mixtures of gases, it is convenient to introduce a quantity called the mole fraction, χ, which is defined as the number of moles of a particular substance in a mixture divided by the total number of moles of all substances present. Mathematically, the mole fraction of a substance A in a mixture with B and C is expressed as
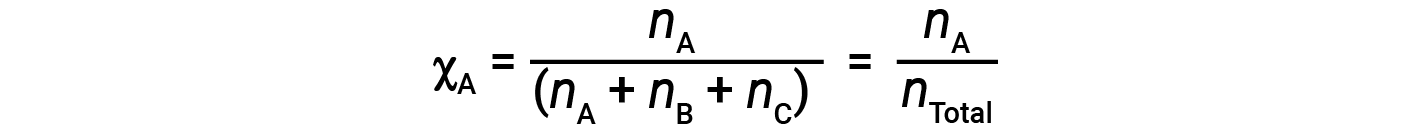
Similarly, the mole fraction of B and C are;
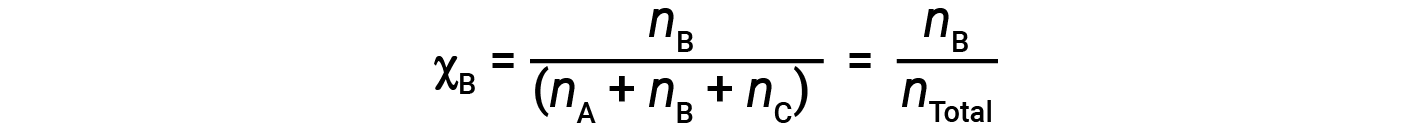
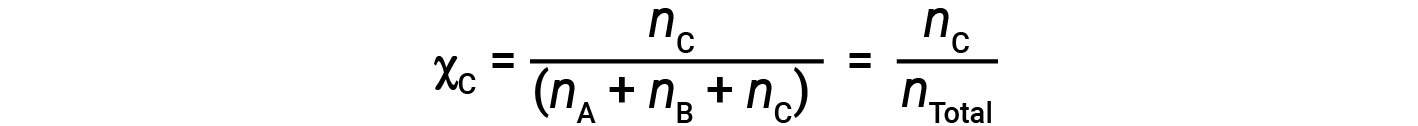
Combining the equation for the mole fraction of A and the equation for partial pressure gives:
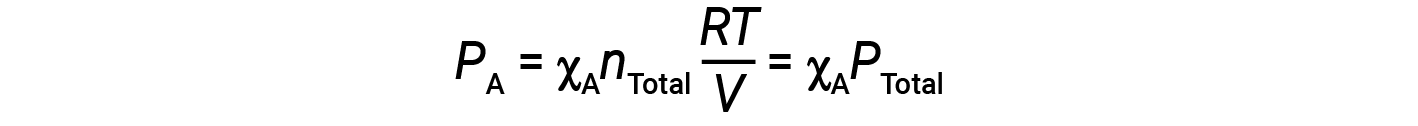
The partial pressure of gas A is related to the total pressure of the gas mixture via its mole fraction.
In other words, the pressure of a gas in a mixture of gases is the product of its mole fraction and the total pressure of the mixture.
This text is adapted from Openstax, Chemistry 2e, Section 9.3: Stoichiometry of Gaseous Substances, Mixtures, and Reactions.


