3.4:
Instantaneous Velocity – II
Instantaneous velocity can be calculated from the position versus time graph. Suppose an object moves from point p1 to point p2. Then its average velocity is given by the slope of the position-time graph.
So, if point p2 approaches point p1, and average x-velocity is calculated over shorter time intervals of delta t, then in the limit as delta t tends to zero, the slope of the tangent to the curve at point p1 represents the instantaneous velocity.
If the tangent to the position-time curve slopes upward or downward to the right, its slope, x velocity, and motion are positive or negative accordingly.
If position as a function of time is known, the instantaneous velocity at any given time can be calculated.
Taking the time derivative of the position function, the velocity as a function of time is estimated. Substituting the value of time, the instantaneous velocity can be obtained.
3.4:
Instantaneous Velocity – II
Instantaneous velocity is the quantity that measures how fast an object is moving along its path. In other words, the instantaneous velocity of an object is the limit of the average velocity as the elapsed time approaches zero, or the derivative of displacement with respect to time. Like average velocity, the instantaneous velocity is a vector with the dimensions of length per unit time. Instantaneous velocity can have both positive and negative values. The instantaneous velocity can be calculated from the position-time graph. The instantaneous velocity at a specific time point is the rate of change of the position function, which is the slope of the position function at that point. The slope of the tangent at any point on the position-time graph equals the velocity at that point. A zero slope indicates that the instantaneous velocity is zero. A positive slope indicates positive instantaneous velocity, while a negative slope indicates a negative instantaneous velocity. The steeper the slope (positive or negative), the greater the particle’s speed in the positive or negative direction.
Consider the motion of a particle in which the position is given by

What is the instantaneous velocity at t = 0.25 s?
The known quantities are the expression for the position as a function of time. To determine the instantaneous velocity, first, consider the equation
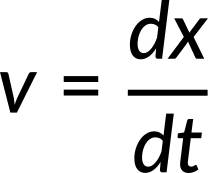
Using the expression of x(t), the expression for velocity is

Substituting the value for time, in the above equation, the instantaneous velocity at 0.25 s is 1.5 m/s.
This text is adapted from Openstax, University Physics Volume 1, Section 3.2: Instantaneous Velocity and Speed.
