3.7:
Kinematic Equations – I
Around us, we see many examples of objects moving with constant acceleration where the rate of change of velocity is the same throughout the motion. For example, a ball falling under gravity has constant acceleration if the effects of air are neglected.
The motion of objects with constant acceleration is approximated by kinematic equations, also known as equations of motion. These equations include variables like displacement, velocity, acceleration, and time.
Recall that acceleration is the change of velocity with time. Now suppose, an object starts moving at time t1 equal to zero seconds with an initial velocity v0x, and after some time t2 equal to t seconds has a final velocity vx.
After substituting these variables, the product of acceleration and time corresponds to the total change in velocity over time t. Thus, the x velocity at any time t is given by the sum of initial velocity and the change in x velocity. This expression for vx is the first fundamental kinematic equation.
3.7:
Kinematic Equations – I
When an object moves with constant acceleration, the velocity of the object changes at a constant rate throughout the motion. The kinematic equations of motions are derived for such cases where the acceleration of the object is constant. The first kinematic equation gives an insight into the relationship between velocity, acceleration, and time. We can see, for example:
- Final velocity depends on how large the acceleration is and how long it lasts
- If the acceleration is zero, then the final velocity equals the initial velocity, as expected (in other words, velocity is constant)
- If acceleration is negative, the final velocity is less than the initial velocity
All these observations fit our intuition. Note that it is always helpful to examine the basic equations in light of our intuition and experience to check that they accurately describe nature.
Consider an airplane landing with an initial velocity of 70 m/s and decelerating at 1.5 m/s2 for 40 seconds. Then, the final velocity of the airplane can be calculated using the first kinematic equation. The known quantities are initial velocity, constant (de)acceleration, and time. By substituting the known values in the equation,
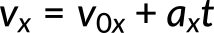
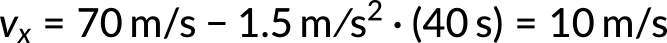
The final velocity of the airplane is 10 m/s.
This text is adapted from Openstax, University Physics Volume 1, Section 3.4: Motion with Constant Acceleration.
