3.14:
Velocity and Position by Integral Method
Velocity and position can be calculated if the acceleration as a function of time is known. The time derivative of the velocity function is acceleration.
So, taking the integral on both sides of the equation, the velocity can be calculated as a function of time. The equation can be rewritten for the case of constant acceleration.
The integration constant can be calculated using the initial conditions. The value of this constant is substituted into the expression for velocity as a function of time to obtain the first kinematic equation.
The time derivative of the position function is the velocity function. Again, taking the integral on both sides of the equation, the position as a function of time is calculated.
Now, the expression for the velocity function is substituted, and the equation is integrated. Applying the initial conditions, the integration constant is derived.
The value of this constant is then substituted into the expression for the position as a function of time to obtain the second kinematic equation.
3.14:
Velocity and Position by Integral Method
If acceleration as a function of time is known, then velocity and position functions can be derived using integral calculus. For constant acceleration, the integral equations refer to the first and second kinematic equations for velocity and position functions, respectively.
Consider an example to calculate the velocity and position from the acceleration function. A motorboat is traveling at a constant velocity of 5.0 m/s when it starts to decelerate to arrive at the dock. Its acceleration is −1/4·t m/s2. Let's determine the procedure to calculate the velocity and position function of the motorboat.
Let's take time, t = 0, when the boat starts to decelerate. Now, the velocity function can be calculated using the integral of the acceleration function

Using the expression of acceleration in the above equation, the velocity as a function of time is calculated to be
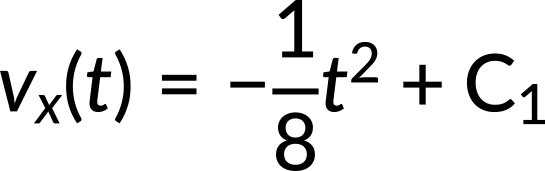
The constant of integration C1 is calculated to be 5 m/s using the value of initial time and velocity.
Hence, the velocity as a function of time reduces to
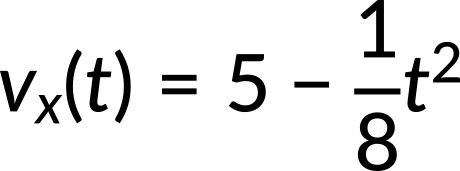
Integrating the derived velocity function with respect to time, the position function is calculated. The position as a function of time is
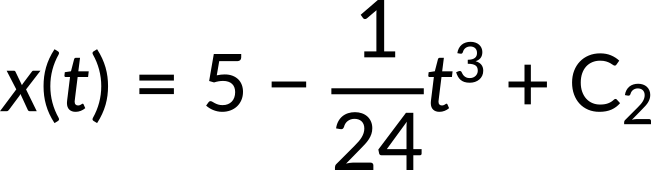
Again, using the initial conditions, the constant of integration C2 is calculated to be zero.
Thus, the position as a function of time reduces to
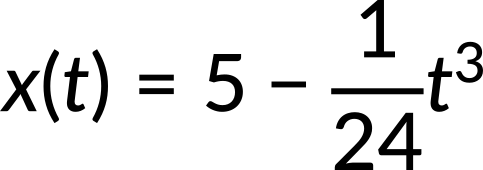
This text is adapted from Openstax, University Physics Volume 1, Section 3.6: Finding Velocity and Displacement from Acceleration.
