4.6:
Projectile Motion: Equations
The motion of a projectile along the horizontal and vertical directions can be analyzed independently by using the equations of motion. Putting ay as minus g and ax as zero for a projectile, the equations simplify.
The initial velocity components obtained by using trigonometric relations further simplify the motion equations.
At the zenith, vy is zero. By substituting vy in the velocity equation for y-direction, time for half-flight is obtained. The zenith height of the projectile can be obtained by substituting the expression for the half-flight time in the displacement equation for y-direction.
The total duration of the flight is twice the time of half-flight. By substituting the total time in the displacement equation in the x-direction, the equation for the maximum range of the projectile is obtained.
The trajectory describes the projectile's path in a 2-dimensional space. Its equation can be obtained by using the position equations.
Rearranging the terms in x-component equation and substituting it in the equation of y-position, we get the final trajectory equation. This equation represents a parabola.
4.6:
Projectile Motion: Equations
Projectile motion is commonly observed in our day-to-day life. For example, a basketball thrown by a player, an arrow shot from a bow, and kids jumping into the pool, all undergo projectile motion.
Any projectile motion problem can be solved by using the following strategy:
- Initially, resolve the motion into horizontal and vertical components along the x– and y-axes. The magnitudes of the components of displacement along these axes are x and y. The magnitudes of the vertical and horizontal components of velocity are given by v⋅sin(θ) and v⋅cos(θ), respectively, where v is the magnitude of the velocity and θ is its direction relative to the horizontal.
- Treat the motion as two independent one-dimensional motions: one horizontal and one vertical. Use the kinematic equations for horizontal and vertical motion presented earlier.
- Solve for the unknowns in the two separate motions. Note that the only common variable between the motions is time, t. The problem-solving procedures here are the same as those for one-dimensional kinematics.
- Recombine quantities in the horizontal and vertical directions to find the total displacement and velocity. Finally, solve for the magnitude and direction of the displacement and velocity using
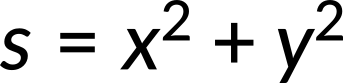
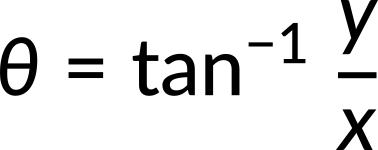
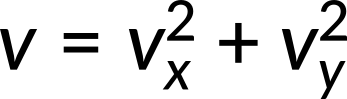
where θ is the direction of the displacement.
This text is adapted from Openstax, University Physics Volume 1, Section 4.3: Projectile Motion.
