4.10:
Relative Velocity in One Dimension
A frame of reference is a coordinate system with a time scale used by the observer to describe the kinematic variables of an object.
The velocity of object A relative to the observer B is given by the vector difference of their velocities relative to the ground G. The measured velocity is the relative velocity.
For an observer standing on the ground, a man walking on a moving walkway appears to move faster.
But for a woman standing on the walkway, the man appears to move, but slower.
If the velocity of the man relative to the walkway is 1 meter per second, and the velocity of the walkway relative to the ground is 2 meters per second, what will be the velocity of the man relative to the ground?
Initially, list the known and unknown quantities. Next, write the relative velocity equation connecting the reference frames. Finally, substitute the known values to solve for the unknown.
4.10:
Relative Velocity in One Dimension
The understanding of the concept of reference frames is essential to discuss relative motion in one or more dimensions. When we say that an object has a certain velocity, we must state the velocity with respect to a given reference frame. In most examples, this reference frame has been Earth. For instance, if a statement reads that a person is sitting in a train moving at 10 m/s east, then it implies that the person on the train is moving relative to the surface of Earth at this velocity, therefore Earth is the reference frame. All discussions of relative motion must define the reference frames involved. Here, we discuss a method to refer to reference frames in relative motion.
Let us first discuss the relative motion in one dimension, since velocity vectors only have two possible directions. Imagine a person is sitting on a train moving east. If east is considered as the positive direction and Earth as the reference frame, then we can write the velocity of the train with respect to the Earth as 10 m/s. Now imagine the person gets out of their seat and walks toward the back of the train at 2 m/s. This tells us that the person has a velocity relative to the reference frame of the train. Since the person is walking west (in the negative direction), their velocity with respect to the train can be written as
where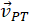 
is the velocity of the person with respect to train and 
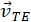is the velocity of the train with respect to Earth. Adding the vectors, we find 
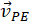, the velocity of the person with respect to Earth to be 8 m/s.
This text is adapted from Openstax, University Physics Volume 1, Section 4.5: Relative Motion in One and Two Dimensions.