6.7:
Dynamics of Circular Motion
Consider a test-tube in a centrifuge, moving with a constant velocity along a circular path of radius, r.
Suppose the test-tube moves through a small angle Δθ, covering arc length, Δr, in time, Δt.
Since the direction of velocity is different at each instance, the triangles formed by the velocity vectors and the radial vectors are similar.
Considering small angles, the magnitude of Δv by v equals Δr by r. Dividing the equation by Δt and rearranging the terms, Δv by Δt equals v by r times Δr by Δt.
Now, at limit Δt tends to 0, Δv by Δt is the acceleration, and Δr by Δt is the linear velocity of the object.
Therefore, the acceleration of any object in uniform circular motion is expressed as the square of linear velocity divided by its radial distance.
The term centripetal acceleration highlights that the object is accelerated towards the center of the circular path at every instant. Multiplying the acceleration with the object's mass gives an expression for the centripetal force on the object.
6.7:
Dynamics of Circular Motion
An object undergoing circular motion, like a race car, is accelerating because it is changing the direction of its velocity. This centrally directed acceleration is called centripetal acceleration. This acceleration acts along the radius of the curved path (thus is also referred to as radial acceleration).
Any acceleration must be produced by some force. Therefore, any force or combination of forces can cause centripetal acceleration. A few examples include the tension in the rope on a tetherball, the force of the Earth's gravity on the Moon, the friction between roller skates and a rink floor, a banked road's force on a car, and the forces on the tube of a spinning centrifuge. Any net force causing uniform circular motion is called a centripetal force. The direction of a centripetal force is always toward the center of curvature, the same as the direction of centripetal acceleration. According to Newton's second law of motion, the net force is equal to the mass multiplied by the acceleration. In the case of uniform circular motion, the acceleration is the centripetal acceleration, and is given by
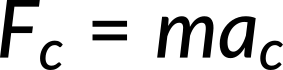
Thus, the magnitude of centripetal force FC is the mass multiplied by the centripetal acceleration. Centripetal force is always perpendicular to the path and points towards the center of curvature, because the centripetal acceleration is perpendicular to the velocity and points towards the center of curvature. By substituting the expression for centripetal acceleration in terms of velocity and the radius of curvature, a relationship between centripetal force and the radius of curvature is obtained.
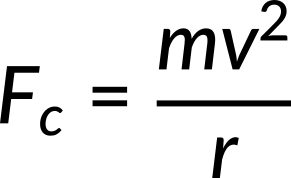
This implies that a large centripetal force causes a small radius of curvature and a sharper curve for a given mass and velocity.
This text is adapted from Openstax, University Physics Volume 1, Section 6.3: Centripetal Force.
