8.9:
Force and Potential Energy in One Dimension
Conservative forces can be expressed in terms of potential energy.
Consider a body moving along a straight line due to a conservative force that is a function of position.
Now, the work done by the conservative force is equal to the negative of the change in its potential energy.
The work done is also equal to the product of force and the displacement caused by the force.
Thus, the force on the body is equal to the negative of the change in potential energy divided by the displacement.
The negative sign indicates that the conservative force drags the system to a lower potential energy.
For very small displacements, the expression for force and potential energy in one dimension can be established.
For verification of the force and potential energy relationship, consider the example of elastic potential energy. When substituted into the force and energy relationship, the formula for Hooke's law is established.
8.9:
Force and Potential Energy in One Dimension
Force can be calculated from the expression for potential energy, which is a function of position. The component of a conservative force, in a particular direction, equals the negative of the derivative of the corresponding potential energy with respect to the displacement in that direction. For regions where potential energy changes rapidly with displacement, the work done and force is maximum. Also, when force is applied along the positive coordinate axis, the potential energy decreases with an increase in displacement. Hence, force and the derivative of potential energy with respect to displacement have opposite signs.
For instance, if the potential energy of a particle undergoing one-dimensional motion along the x-axis is

where c = 8 N/m3, what will the force be for the given potential energy? Here, the known quantity is potential energy. The unknown quantity force needs to be calculated.
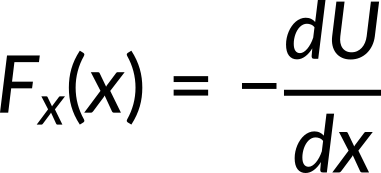
Incorporating the value of potential energy in the above expression, the force along the x-direction is calculated to be −cx3. Substituting the value of c, the force is calculated to be −8x3.
The potential energy function for the force between two atoms in a diatomic molecule is approximately given by
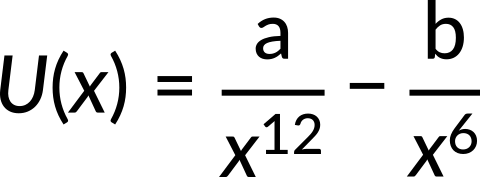
where a and b are constants and x is the distance between the atoms. If the dissociation energy of the molecule is
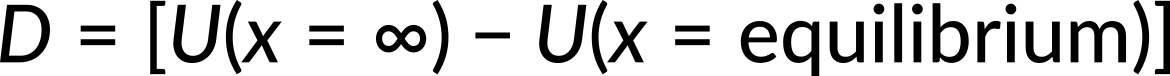
what is the value of D? Here, the known quantity is the potential energy. The unknown quantity is the dissociation energy of the molecule. Substituting the potential energy function, we get the expression for force. Since the net force is zero at equilibrium, we get
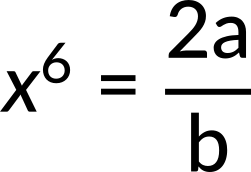
Now, the value of x6 is substituted in the expression for potential energy. Since potential energy at infinity is zero, the dissociation energy of the molecule is calculated to be b2/4a.
This text is adapted from Openstax, University Physics Volume 1, Section 8.4: Potential Energy Diagrams and Stability.
