9.6:
Conservation of Momentum: Problem Solving
Consider a 50 kilogram stationary cannon. A shell of mass 5 kilograms is fired from the cannon which travels with a velocity of 400 meters per second. What will be the velocity of the cannon after firing, ignoring frictional forces?
The mass and velocity of the shell and the mass of the cannon are the known quantities. The velocity of the cannon is the unknown quantity. Ignoring frictional forces, the cannon and the shell will form a closed system.
The positive x-axis is assumed in the direction of the shot to define the velocity vectors. Since the cannon and shell are stationary, the momentum before the interaction is zero.
After firing the shell, the final momentum will be equal to the sum of the cannon's momentum and the shell's momentum.
Lastly, equate the momentum before and after the interaction to obtain the unknown quantity. Here, the velocity of the cannon after firing is resolved by substituting the known quantities in the equation and it comes out to be minus 40 meters per second.
The negative sign indicates that the cannon recoils in the direction opposite to the direction of the shot.
9.6:
Conservation of Momentum: Problem Solving
Solving problems using the conservation of momentum requires four basic steps:
- Identify a closed system, where the total mass is constant, and no net external force acts on it.
- Write down an expression representing the total momentum of the system before the interaction.
- Write down an expression representing the total momentum of the system after the interaction.
- Equate these two expressions to obtain the unknown quantity.
Let us apply these steps to solve a problem. Suppose two carts in a physics lab roll on a level surface with negligible friction. These carts have small magnets at their ends so that when they collide, they stick together. The first cart has a mass of 675 g and is rolling at 0.750 m/s to the right; the second has a mass of 500 g and is rolling at 1.33 m/s, also to the right. After the collision, what is the velocity of the two joined carts?
The system of two carts meets the requirements for a closed system: the combined mass of the two carts does not change, and while the carts exert forces on each other, those forces are internal to the system, so they do not change the momentum of the system as a whole. In the vertical direction, the weights of the carts are canceled by the normal forces on the carts from the track.
Here, the known quantities are the mass of cart 1 (m1 = 675 g), mass of cart 2 (m2 = 500 g), initial velocity of cart 1 (v1 = 0.750 m/s) and initial velocity of cart 2 (v2 = 1.33 m/s). The unknown quantity, the final velocity vf of the joined carts, needs to be calculated. As per the conservation of momentum, the initial momentum is equal to the final momentum. The direction of their initial velocity vectors is defined to be in the +x-direction. The initial momentum is then given by:
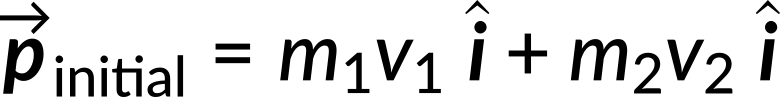
The final momentum of the joined carts is
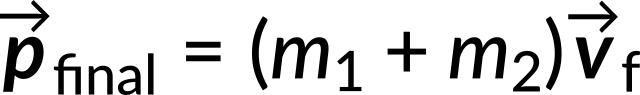
Equating both these equations, the final velocity is given by
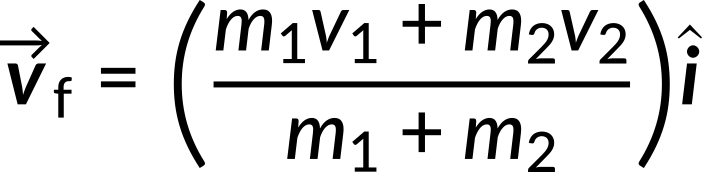
Substituting the known quantities in the above expression, the final velocity is 0.997 m/s in the x-direction.
This text is adapted from Openstax, University Physics Volume 1, Section 9.3: Conservation of Linear Momentum.
