9.10:
Elastic Collisions: Case Study
Suppose marble A and B undergo one-dimensional collision. From the conservation of momentum and kinetic energy, the equation of elastic collision can be written.
If marble B is initially at rest, then the equations get simplified. On solving the two equations, the final velocity of the marbles A and B can be obtained.
If marbles of equal masses collide, then marble A comes to rest after the collision and B travels with the initial velocity of marble A. By solving the equations, it is seen that marbles exchange momentum.
If marble B is heavier than marble A, then, after collision, marble A bounces back with almost the same velocity, and marble B moves with a very low velocity.
If marble A is heavier than marble B, then marble A continues to move with the same velocity. Marble B gets a push and travels with a higher velocity than the initial velocity of marble A.
In the case of marbles of different masses undergoing one-dimensional elastic collisions, the relative velocities before and after the collision have the same magnitude but opposite direction.
9.10:
Elastic Collisions: Case Study
Elastic collision of a system demands conservation of both momentum and kinetic energy. To solve problems involving one-dimensional elastic collisions between two objects, the equations for conservation of momentum and conservation of internal kinetic energy can be used. For the two objects, the sum of momentum before the collision equals the total momentum after the collision. An elastic collision conserves internal kinetic energy, and so the sum of kinetic energies before the collision equals the sum after the collision. We can understand this better with the help of a problem.
Let’s try to calculate the velocities of two objects following an elastic collision, given that mA = 0.50 kg, mB = 3.5 kg, vA1x = 4.0 m/s, and vB1x = 0 m/s.
The initial conditions imply that a small object strikes a larger object that is initially at rest. There are two unknowns (the final velocities vA2x and vB2x), which should be found. Because this collision is elastic, the equations for conservation of momentum and conservation of energy can be used. They are given by,
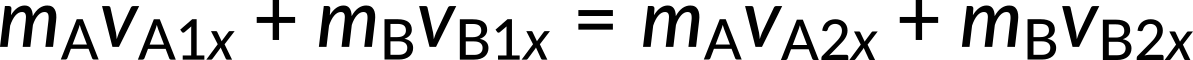
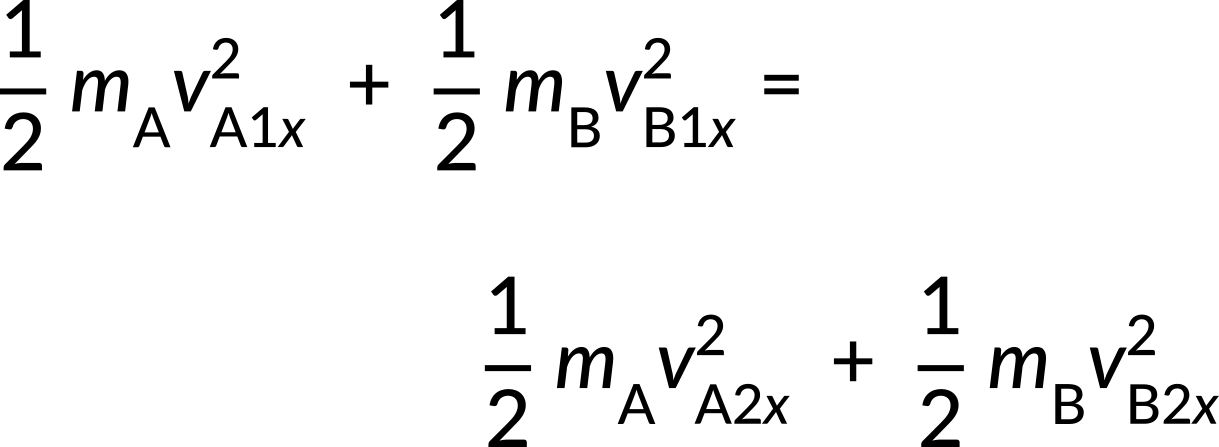
Both can be simplified because object B is initially at rest, and thus vB1x = 0 m/s.
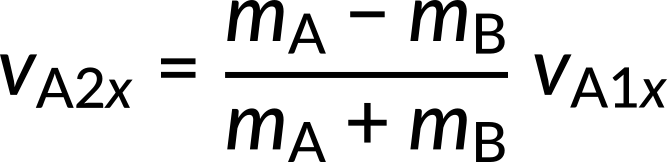
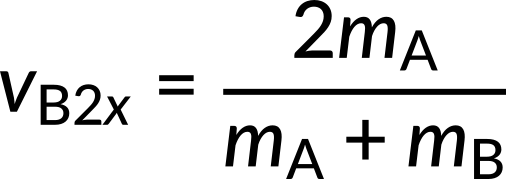
Substituting the known values into these equations, we obtain vA2x = -3 m/s and vB2x= 4 m/s. The negative sign indicates that the first object bounces backward. The result of this example is reasonably intuitive: a small object strikes a larger one at rest and bounces backward. The larger one is knocked forward but with a low speed. This is like a compact car bouncing backward off a full-size SUV that is initially at rest.
This text is adapted from Openstax, University Physics Volume 1, Section 9.4: Types of Collisions.
