14.17: Kepler's Third Law of Planetary Motion
In the early 17th century, German astronomer and mathematician Johannes Kepler postulated three laws for the motion of planets in the solar system. In 1909, he formulated his first two laws based on the observations of his forebears, Nikolaus Copernicus and Tycho Brahe. However, in 1918, he published his third law of planetary motion, which gives a precise mathematical relationship between a planet's average distance from the Sun and the amount of time it takes to revolve around the Sun. It states that
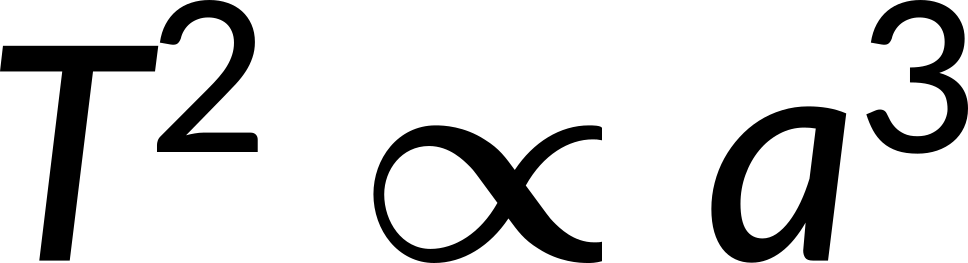
The proportionality constant for this law was derived much later, after Newton established the universal law of gravitation. However, Kepler formatted this third law of planetary motion based on the observation of Galilean moons orbiting Jupiter.
This law established the ratios of the average distances of each planet from the Sun, to the Earth's average distance from the Sun, as shown in Table 1.
Table 1: Ratio of Planetary Distances from the Sun Compared to the Earth-Sun Distance.
| Material | Planetary Distance Ratio |
| Mercury | 0.387 |
| Venus | 0.723 |
| Earth | 1.000 |
| Mars | 1.520 |
| Jupiter | 5.200 |
| Saturn | 9.570 |
| Uranus | 19.170 |
| Neptune | 30.180 |
The actual value for the distance of the Earth from the Sun was calculated for the first time during a transit of Venus using the parallax method. Using this value of the astronomical unit, the actual distances to all other planets were obtained. This law is very useful to estimate the distances of all the satellites around the Jovian planets, just by observing their time periods.
This text is adapted from Openstax, University Physics Volume 1, Section 13.5 Kepler’s Laws of Motion.
