15.12:
Damped Oscillations
When a wood log floating on the surface of water is pushed downward and is allowed to bob up and down, it oscillates about its mean position with a constant amplitude similar to simple harmonic motion.
Over time, a dissipative force known as the damping force exerted by the water reduces the amplitude of oscillation with some energy loss, corresponding to its motion, and results in damped harmonic oscillations.
The damping force is proportional to the wood log's velocity, which is the measure of oscillation decay directed opposite to the motion.
The net force equals the restoring and damping forces, which act in the opposite directions.
Rearranging and rewriting the velocity and acceleration equation in terms of derivatives of position with respect to time leads to a differential quadratic equation, which describes the damped harmonic motion of the wood log.
15.12:
Damped Oscillations
In the real world, oscillations seldom follow true simple harmonic motion. A system that continues its motion indefinitely without losing its amplitude is termed undamped. However, friction of some sort usually dampens the motion, so it fades away or needs more force to continue. For example, a guitar string stops oscillating a few seconds after being plucked. Similarly, one must continually push a swing to keep a child swinging on a playground.
Although friction and other non-conservative forces can be made negligibly small, complete undamped motion is rare. In fact, these non-conservative forces are often required to dampen oscillations, such as in-car shock absorbers. For a system that has a small amount of damping, the period and frequency are nearly the same as for simple harmonic motion, but the amplitude gradually decreases. This occurs because the non-conservative damping force removes energy from the system, usually in the form of thermal energy. In general, energy removal by non-conservative forces is described as
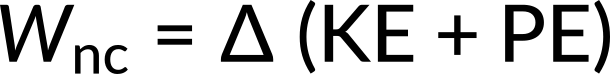
where Wnc is work done by a non-conservative force (here, the damping force). For a damped harmonic oscillator, Wnc is negative because it removes mechanical energy (KE + PE) from the system.
This text is adapted from Openstax, College Physics, Section 16.7: Damped Harmonic Motion and Openstax, University Physics Volume 1, Section 15.4: Damped Oscillations.
