23.2: Calculation of Electric Flux
Consider the electric field of an oppositely charged, parallel-plate system and an imaginary box between those plates. Let the bottom face of the box be ABCD, and the top face be FGHK. The electric field between the plates is uniform and points from the positive plate toward the negative plate. The calculation of this field's flux through the box's various faces shows that the net flux through the box is zero. Why does the flux cancel out here?
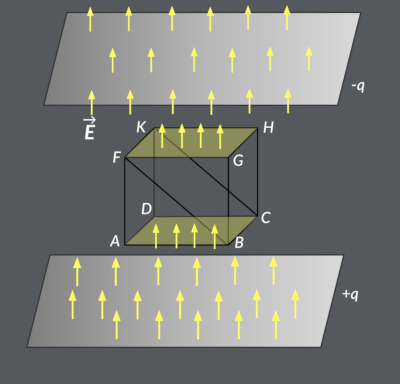
The electric flux through the bottom face becomes negative as the electric field is in the opposite direction compared to the surface's normal vector. Conversely, the electric flux through the top face becomes positive as the electric field and the normal are in the same direction. The electric flux through the other faces is zero since the electric field is perpendicular to the normal vectors of those faces. The net electric flux through the box is the sum of the fluxes through the six faces. Here, the net flux through the box is equal to zero. The magnitude of the flux through the rectangle BCKF inside the box equals the magnitudes of the flux through both the top and bottom faces.
In brief, the reason for the flux canceling out is that the electric field sources are outside the box. This means that if the electric field line enters the box's volume, it must also exit somewhere on the surface because there is no charge inside for the lines to land on. Therefore, generally, the electric flux through a closed surface is zero if there are no electric field sources, including either positive or negative charges, inside the enclosed volume.
