24.6:
Calculations of Electric Potential I
Consider a spherical conductor with a radius of 20 centimeters and a charge of 40 micro-coulombs. What would be the electric potential at radial distances of 60 and 10 centimeters?
According to Gauss's law, the electric field inside the sphere is zero. So, to move a test charge within the sphere no work is done. The electric potential is constant inside the sphere and its value is the same as the potential at the surface.
Outside the sphere, the electric field follows the inverse square law. The electric potential is the integral of the dot product of the electric field and the displacement. At an infinite distance, the potential is defined as zero. This gives potential which varies inversely with the radial distance.
So, the electric potential is continuous, but the electric field is discontinuous.
Here, the known quantities are the sphere's radius, epsilon zero, and the charge. The unknown quantities are the electric potential at the two distances. By substituting the known quantities, the potential at 60 centimeters and at 10 centimeters are calculated.
24.6:
Calculations of Electric Potential I
Consider a ring of radius R with a uniform charge density λ. What will the electric potential be at point M, which is located on the axis of the ring at a distance x from the center of the ring?
The ring is divided into infinitesimal small arcs such that point M is equidistant from all the arcs. Here, the cylindrical coordinate system is used to calculate the electric potential at point M. A general element of the arc between angles θ and θ + dθ is of the length Rdθ and has a charge of λRdθ.
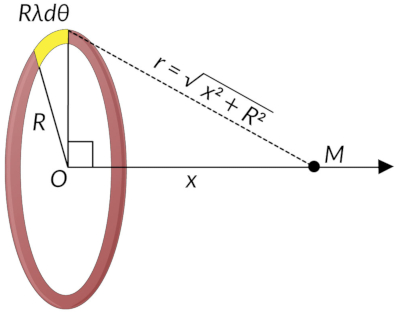
The distance between this element of the ring and the point M is
The potential at point M due to the charge on the whole ring is
Integrating the above equation over the limits gives,
Here, 2πRλ accounts for the whole charge on the ring; therefore, the above equation can be written as
This result is expected because point M is equidistant from all the infinitesimal ring elements, and the total potential will be similar to if the total charge were positioned at a common distance from point M.
Suggested Reading
- Young, H.D. and Freedman, R.A. (2012). University Physics with Modern Physics. San Francisco, CA: Pearson; section 23.3; page 770.
- OpenStax. (2019). University Physics Vol. 2. [Web version]. Retrieved from https://openstax.org/details/books/university-physics-volume-2; section 7.3; page 313.
