33.9:
Energy Carried By Electromagnetic Waves
The energy density corresponding to electric and magnetic fields of an electromagnetic wave is proportional to the square of the respective field magnitudes.
Thus, the total energy density equals the sum of the energy density of both fields. Using the relation between the fields, the expression for energy density shows that the energy due to the individual fields is equal and total energy density is double the energy density due to an individual field.
Now, consider an area perpendicular to the direction of propogation. The distance traveled and the energy passing through the volume in a small interval due to the wavefront can be determined.
From this, the energy flow per unit area per unit time, or the energy flux, can be obtained.
In general, energy flux is defined as the cross-product of the electric and magnetic fields. This quantity is known as the Poynting vector.
It is directed along the electromagnetic wave propagation, and its magnitude gives the rate of energy flow.
33.9:
Energy Carried By Electromagnetic Waves
Anyone who has used a microwave oven knows there is energy in electromagnetic waves. Sometimes, this energy is obvious, such as in the summer sun's warmth. At other times, it is subtle, such as the unfelt energy of gamma rays, which can destroy living cells. Electromagnetic waves bring energy into a system through their electric and magnetic fields. These fields can exert forces and move charges in the system and, thus, do work on them. However, there is energy in an electromagnetic wave, whether absorbed or not. Once created, the fields carry energy away from a source. If some energy is later absorbed, the field strengths are diminished, and anything left travels on. Clearly, the greater the strength of the electric and magnetic fields, the more work they can do and the greater the energy the electromagnetic wave carries. In electromagnetic waves, the amplitude is the maximum field strength of the electric and magnetic fields. The wave energy is determined by the wave amplitude. For a traveling plane wave, its energy will be the sum of the energies of the constituent electric and magnetic fields. The energy per unit volume, or the energy density of the electromagnetic wave, is the sum of the energy density from the electric field and the energy density from the magnetic field.
Using the relationship between electric fields, magnetic fields, and the speed of light, the magnetic field energy can be written in terms of electric energy density, and they are found to be equal to each other. For an electromagnetic wave traveling along the x-axis, the expression for energy density is,
This energy density moves with the electric and magnetic fields in a similar manner to the waves themselves. The rate of transport of energy flux through a surface is defined by a vector quantity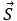 
known as the Poynting vector. The expression for 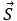is given by
Suggested Reading
- OpenStax. (2019). University Physics Vol. 2. [Web version]. Retrieved from 16.1 Maxwell’s Equations and Electromagnetic Waves – University Physics Volume 2 | OpenStax