20.18:
Maxwell’s Thermodynamic Relations
Consider the differential form of thermodynamic potentials; Maxwell's equations can be derived from thermodynamics potentials.
Internal energy is a function of entropy and volume. Since it is an exact differential, its second-order derivative with respect to volume and entropy does not depend on the order of differentiation.
Substituting the expressions of temperature and pressure gives the first Maxwell's relation.
Enthalpy depends on entropy and pressure. Taking the second-order derivative and substituting the expressions for temperature and volume gives the second Maxwell's relation.
Helmholtz free energy depends on volume and temperature. Expressing it as a second-order derivative and substituting the expressions of pressure and entropy gives the third Maxwell's relation.
Gibbs free energy is a function of pressure and temperature. Differentiating it twice and substituting the relations of volume and entropy gives the fourth Maxwell's relation.
Maxwell's equations are used to solve complex thermodynamic problems as they relate a partial differential between quantities that are hard to measure experimentally to a partial differential between easily measurable quantities.
20.18:
Maxwell’s Thermodynamic Relations
Maxwell's thermodynamic relations are very useful in solving problems in thermodynamics. Each of Maxwell's relations relates a partial differential between quantities that can be hard to measure experimentally to a partial differential between quantities that can be easily measured. These relations are a set of equations derivable from the symmetry of the second derivatives and the thermodynamic potentials.
All thermodynamic potentials are exact differentials. Therefore, their second-order derivative does not depend on the order of differentiation. In the case of Maxwell's relations, the thermodynamic potential is expressed in terms of the partial derivatives of that function. Substituting the values of the partial derivatives gives Maxwell's equations. The four Maxwell's relations are:
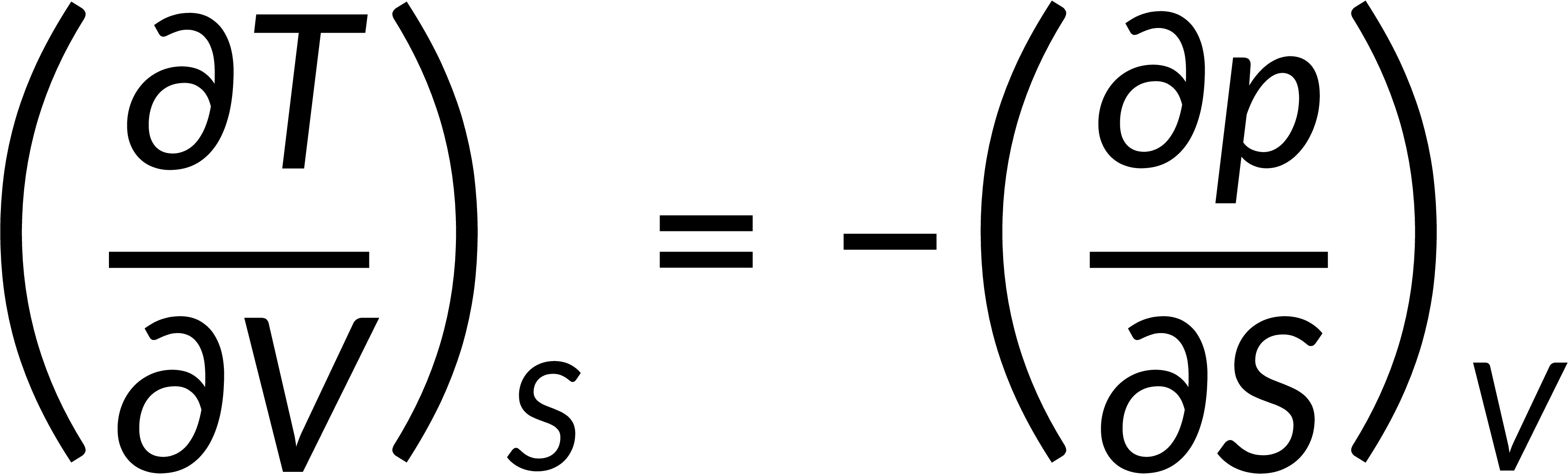
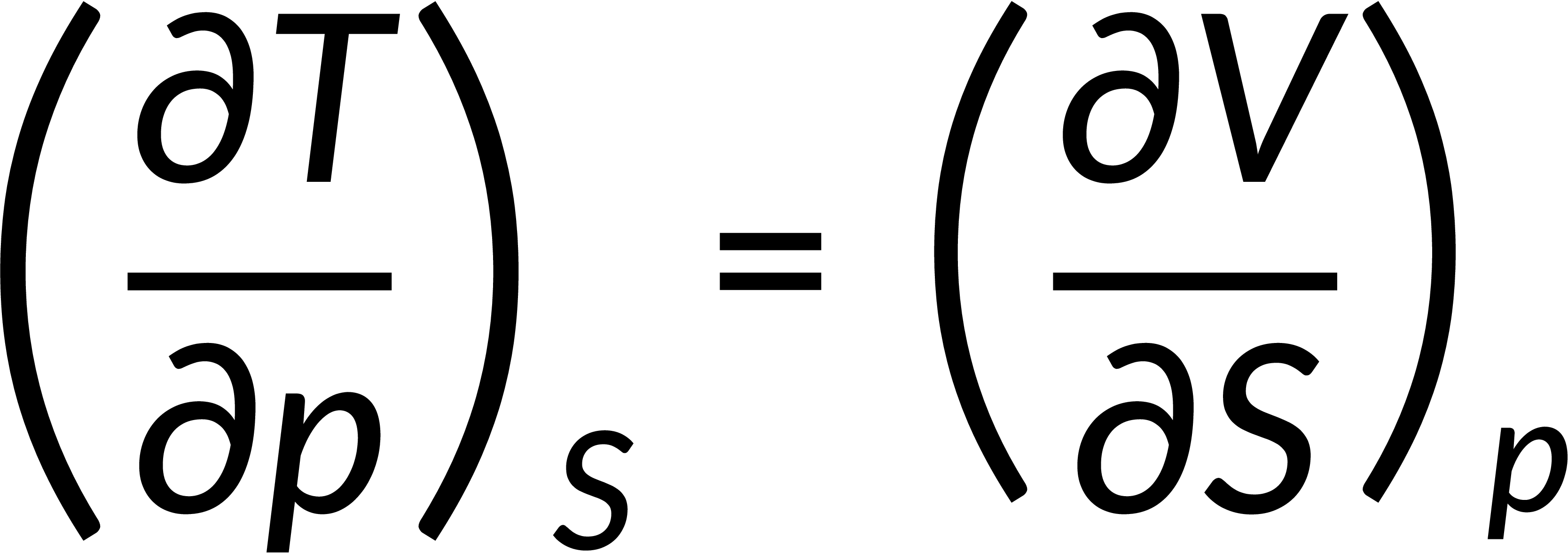
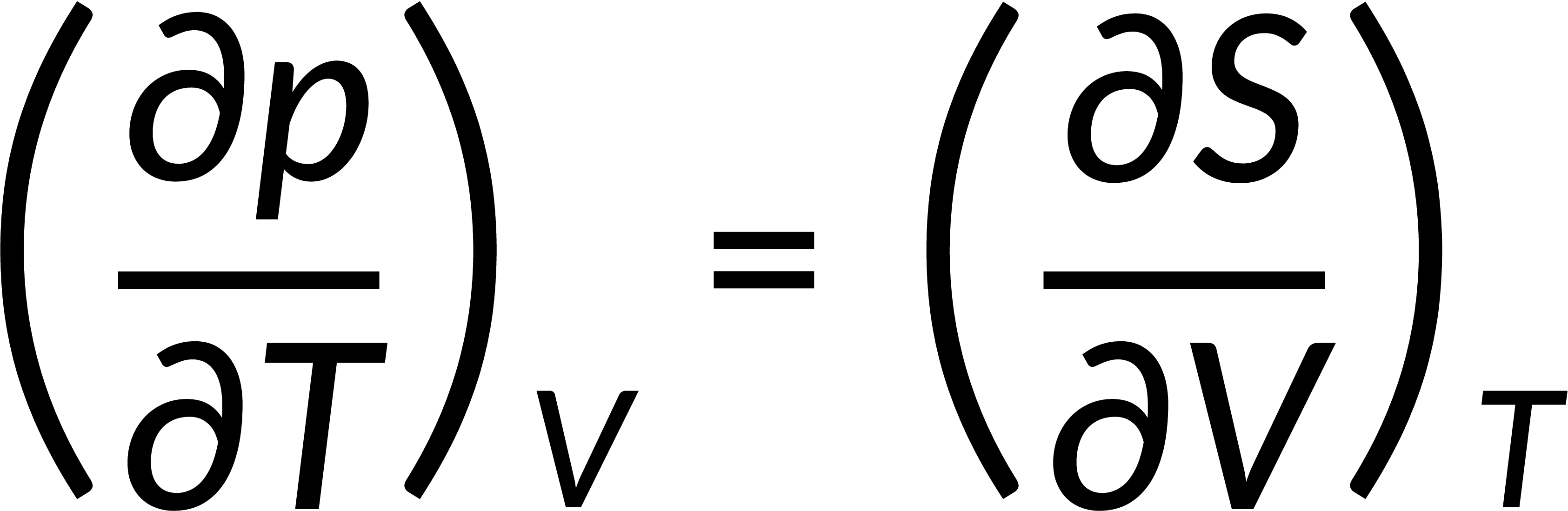
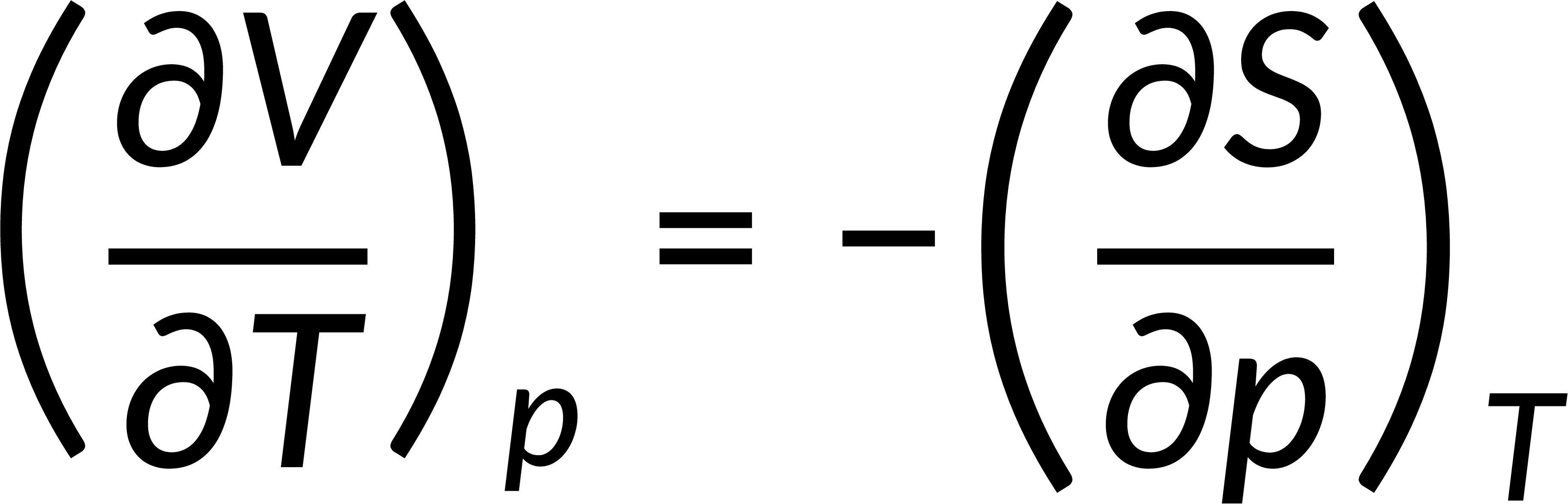
These equations relate entropy changes, which are difficult to measure, with changes in other thermodynamic variables, like temperature, volume, and pressure, that are easier to measure. For example, in the last equation, the left-hand side term gives the change in pressure with the temperature at constant volume. This quantity can be easily measured in a laboratory. However, the term on the right-hand side of the equation is more complicated, as it is hard to measure the entropy change with volume at a constant temperature.
Suggested Reading
- Blundell, S.J. and Blundell, K.M. (2010). Concepts in Thermal Physics. Second Edition. New York, US: Oxford University Press. Pp. 179.
- Helrich, C.S. (2009). Modern Thermodynamics with Statistical Mechanics. Second Edition. Berlin: Springer. Pp. 69.
