23.12: Electric Field of Parallel Conducting Plates
Gauss' law relates the electric flux through a closed surface to the net charge enclosed by that surface. Gauss's law can be applied to find the electric field and the charge enclosed in a region depending on its charge distribution.
Consider a cross-section of a thin, infinite conducting plate having a positive charge. For such a large thin plate, as the thickness of the plate tends to zero, the positive charges lie on the plate's two large faces. Without an external electric field, the charges spread uniformly on these faces, generating an electric field directed away from the plate. If an identical negatively charged plate with the same surface charge density is brought closer to the positively charged plate, the charges on either plate attract each other. The negatively charged plate sets up an electric field directed toward itself. Thus, the net electric field is directed toward the negative plate at any point between the plates. Its magnitude is twice that of an individual plate and is given by
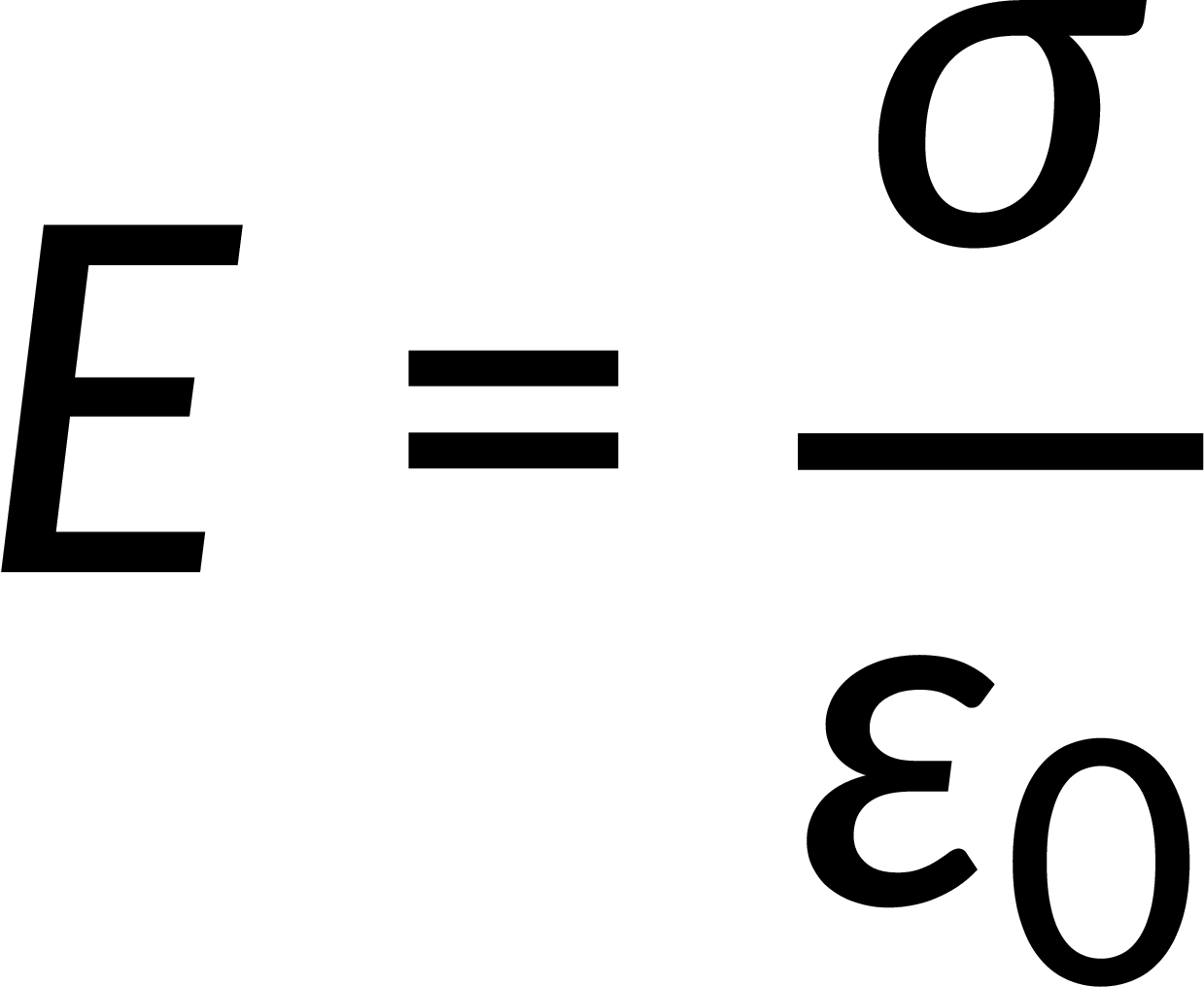
However, at the outer faces of the plates, the electric field due to the positively charged plate is opposite to that of the negatively charged plate; therefore, the electric field on the outer faces of both plates is zero.
If both conducting plates are likely charged, the electric field between the plates is oppositely directed. Hence, it vanishes. However, it is non-zero at the outer faces of the plates.
The expression for the electric field at any point between the plates is also valid for a finite pair of conducting plates as long as points of observation are not close to their edges. Near an edge, planar symmetry breaks down. The field lines are curved (said to be an edge effect of fringing), and the fields become complicated to express algebraically.
