24.14:
Electrostatic Boundary Conditions
The electric field across a homogenous medium is continuous, but while crossing a boundary between two media, it becomes discontinuous. The difference between the field components above and below the boundary gives the change in the field.
Consider a Gaussian pillbox on the surface boundary. Applying Gauss's law, the surface integral can be written as the sum of the integrals over individual faces.
If the thickness of the pillbox tends to zero, only the faces parallel to the boundary contribute. Simplifying this gives the discontinuity of the normal component of the electric field at any boundary.
For the tangential component, consider a thin loop on the boundary. The integration of the electric field over this closed path is zero. Neglecting the contributions along the thickness implies that the tangential component is always continuous across a boundary.
Combining these expressions, the field at the boundary can be written by defining a unit vector.
The line integral of the field from below to above the surface tends to zero, implying that potential is continuous across any boundary.
24.14:
Electrostatic Boundary Conditions
Consider an external electric field propagating through a homogeneous medium. When the electric field crosses the surface boundary of the medium, it undergoes a discontinuity. The electric field can be resolved into normal and tangential components. The amount by which the field changes at any boundary is given by the difference between the field components above and below the surface boundary.
The surface integral of an electric field is given by Gauss's law in integral form and is related to the total enclosed charge. Consider a Gaussian pillbox on the surface boundary. The surface integral of the field is the sum of the integrals over all the surfaces of the pillbox. If the thickness of the pillbox tends to zero, then the surface integral includes only the contributions of the pillbox faces above and below the boundary. Solving this gives the discontinuity of the normal component of the electric field at any surface boundary.
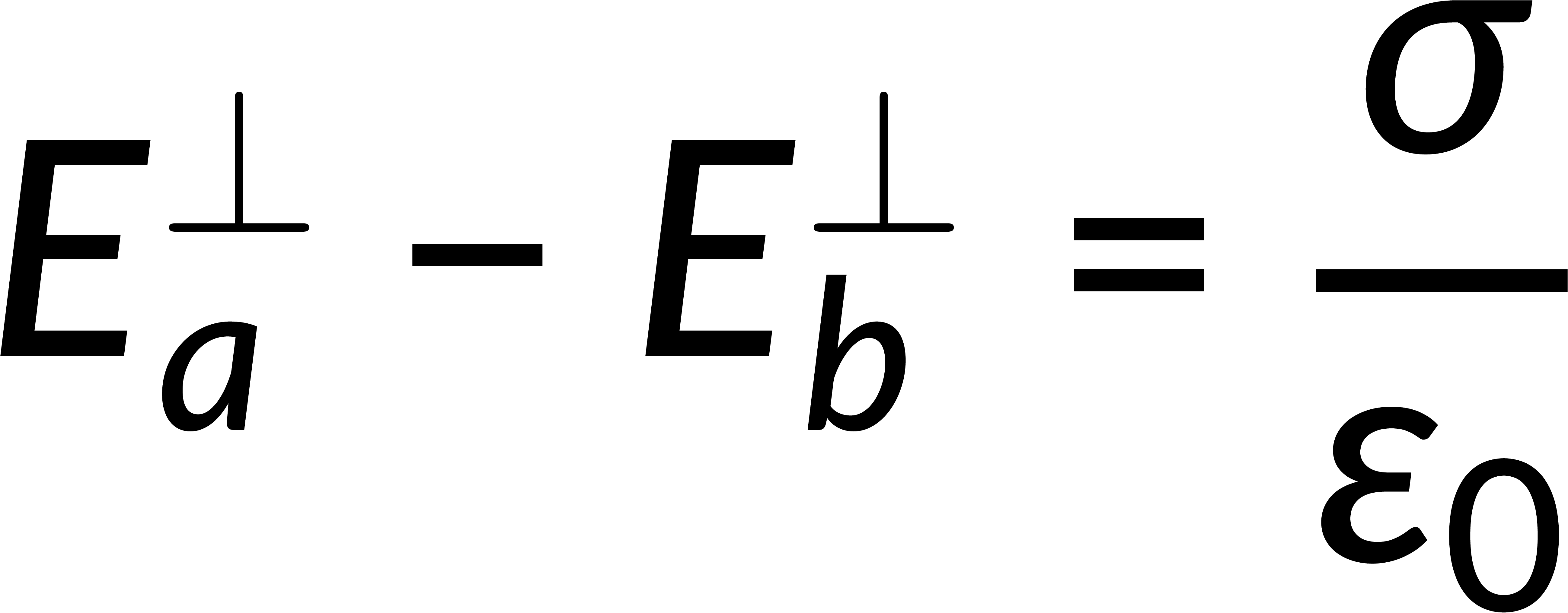
To estimate the discontinuity of the tangential component, consider a loop on the surface boundary. The integration of the electric field over this closed path is zero. Breaking this into the contributions from four parts of the loop and applying the condition that the thickness of the loop tends to zero implies that the tangential component of the electric field is continuous across the boundary.
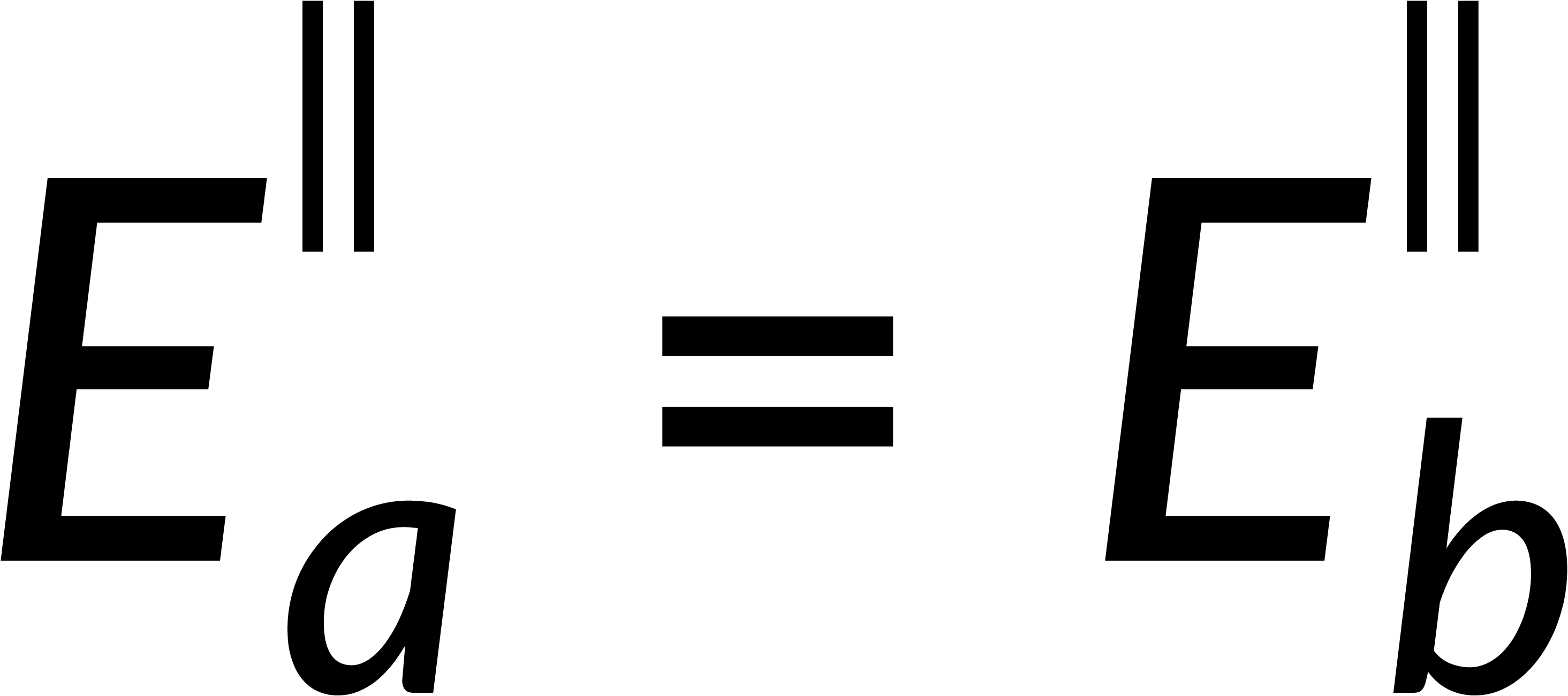
Combining the normal and tangential equations, the field at the boundary can be written by defining the unit vector perpendicular to the surface. It is known that the electric field is the negative gradient of the potential. The line integral of the field from below to above the boundary tends to zero, implying that the potential is continuous across any boundary.
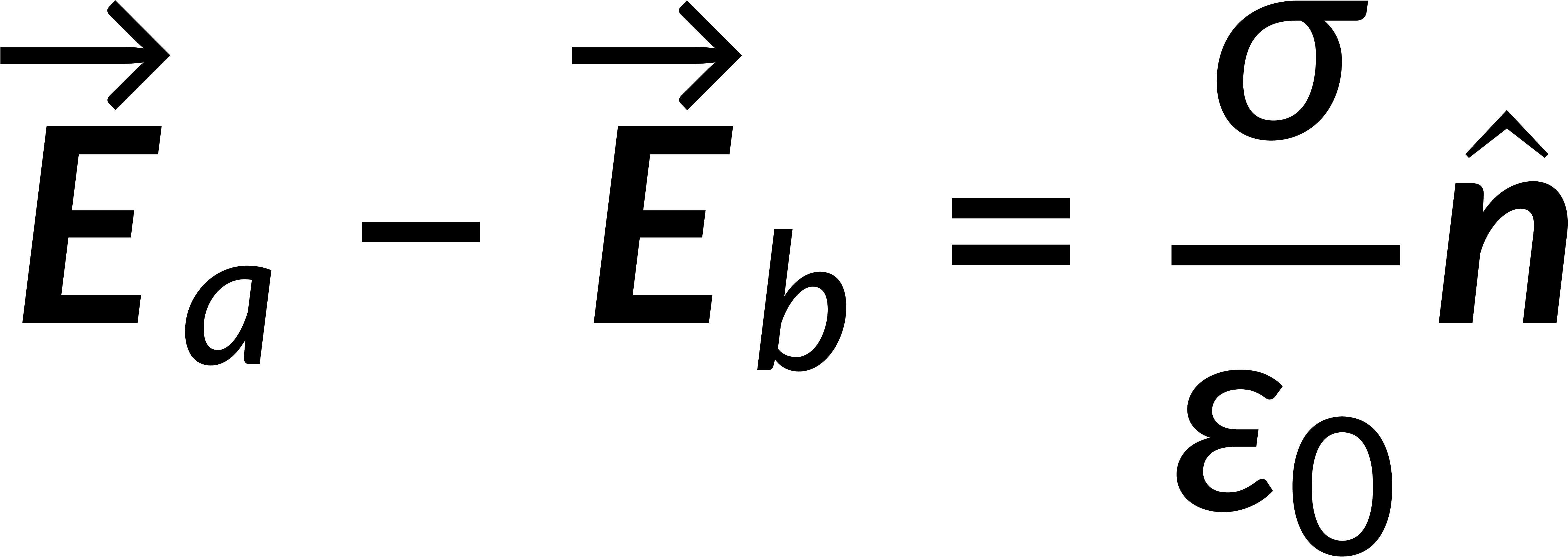
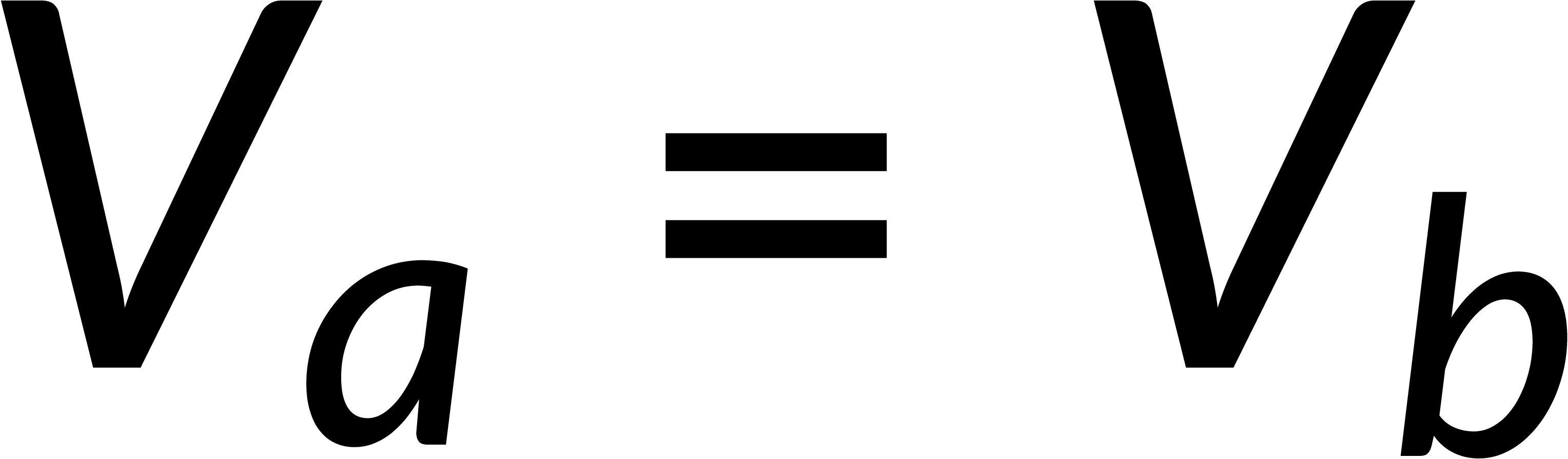
Suggested Reading
- David J. Griffiths (2013) Introduction to Electrodynamics, Fourth Edition: Pearson. Pp. 88-90.
