26.11:
Boundary Conditions for Current Density
The current density becomes discontinuous across an interface having different electrical conductivities.
For steady currents, the divergence of the current density is zero. So, the normal component of the current density is continuous across the boundary.
Recall that the tangential component of the electric field is continuous across an interface. Expressing the electric field in terms of the current density and the electrical conductivity gives the boundary condition for the tangential component of the current density.
Now, the normal component of the electric displacement is discontinuous across the interface. So, the normal component of the electric field is also discontinuous across an interface.
Again, using the expression of the electric field and current density, the boundary condition for the normal component of the current density is obtained in terms of permittivity and conductivity.
It shows that a surface charge density is created across an interface having different conductivities and/or permittivities.
The surface charge density is zero for an interface with the same conductivity and permittivity values or with an equal ratio of permittivity to conductivity.
26.11:
Boundary Conditions for Current Density
Current density becomes discontinuous across an interface of materials with different electrical conductivities. The normal component of the current density is continuous across the boundary.
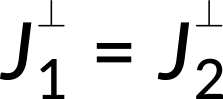
However, the tangential components of the current density are discontinuous across the interface.
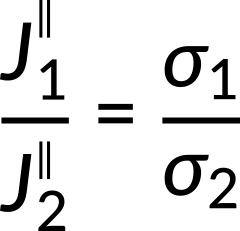
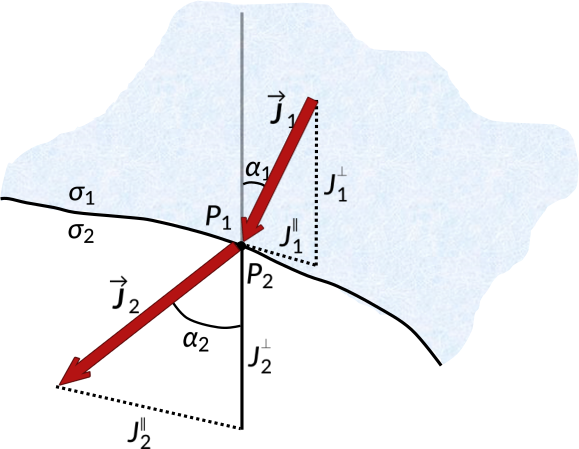
Consider an interface separated by two conducting media with conductivities σ1 and σ2. The steady current density at the interface is 
, in medium 1 at a point P1. It makes an angle α1 with the normal. The current density 
at point P2 in medium 2 makes an angle α2 with the normal.
The normal and tangential components of the current density give the equations as follows:
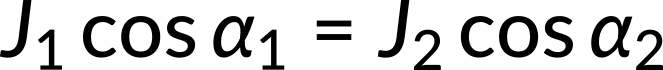
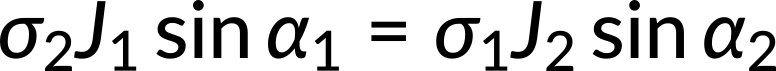
Taking the ratio of the two equations, the expression for the electrical conductivities in both the media is obtained.
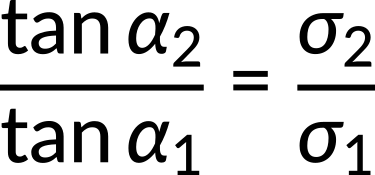
If the electrical conductivity of medium 1 is greater than that of medium 2, the angle α2 approaches zero. This implies that the current density is normal to the surface of conductor 1.
Suggested Reading
- Ida, Nathan, Engineering Electromagnetics, 3rd Edition, Springer. Pp. 355-356
- Cheng, David K., Field and Wave Electromagnetics, Addison-Wesley Publishing Company, Pp. 183.