29.5:
Magnetic Field Due to Two Straight Wires
Consider two infinitely long, parallel conductors carrying current in opposite directions. What is the net magnetic field midway between the conductors?
The magnetic field lines form concentric circles, and the field at the midpoint between both conductors acts in the same direction.
The magnetic field due to a straight conductor is directly proportional to the current flowing through it, and inversely proportional to its distance from the conductor.
However, according to the principle of magnetic field superposition, the net magnetic field due to multiple conductors is the vector sum of the field due to the individual conductors.
So, the net magnetic field magnitude midway between the conductors is proportional to the sum of the current's magnitude in the individual conductor.
The magnetic field magnitudes at any arbitrary point from either conductor can be estimated using the principle of superposition.
For points very far from the conductors, the equations become simplified.
So, the net field magnitude due to two conductors drops more rapidly with distance than in the case of a single conductor.
29.5:
Magnetic Field Due to Two Straight Wires
Consider two parallel straight wires carrying a current of 10 A and 20 A in the same direction and separated by a distance of 20 cm. Calculate the magnetic field at a point "P2", midway between the wires. Also, evaluate the magnetic field when the direction of the current is reversed in the second wire.
The current flowing in the wires and the separation distance between the wires are the known quantities. The magnetic field at a point 10 cm from each wire must be evaluated.
The magnetic field lines form counterclockwise concentric circles around the wires. The expression for the magnetic field due to wire 1 and wire 2 is given by,
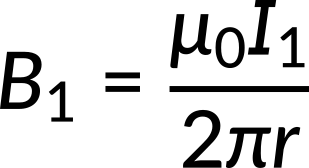
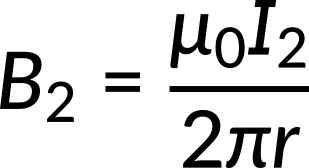
The magnetic fields due to both the current-carrying wires point in opposite directions at the midpoint between both wires. According to the principle of magnetic field superposition, the net magnetic field due to multiple conductors is the vector sum of the field due to the individual conductors. Thus, the net magnetic field is the difference between the magnetic fields for both wires. When the expression for the magnetic field for the individual wires is substituted, the net magnetic field expression reduces to,
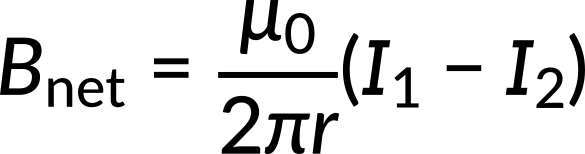
After substituting the current and distance values, the net magnetic field is calculated as −2 x 10−5 T when the current flows in the same direction in both wires.
When the current direction is reversed in the second wire, the magnetic fields due to both wires point in the same direction at the midpoint. Therefore, applying the principle of magnetic field superposition, the net magnetic field at the midpoint is expressed as,
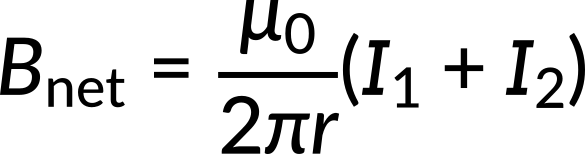
After substituting the current and distance values, the net magnetic field is calculated as 6 x 10−5 T when the current flows in opposite directions in both wires.
Suggested Reading
- Young, H.D and Freedman, R.A. (2012). University Physics with Modern Physics. San Francisco, CA: Pearson. Pp. 930
- OpenStax. (2019). University Physics Vol. 1. [Web version] Pp 542.
