29.15:
Potential Due to a Magnetized Object
When placed in an external magnetic field, a magnetic material shows the alignment of the magnetic dipoles. This state of magnetic polarization, called magnetization, is the magnetic dipole moment per unit volume.
Consider a thin slab of uniformly magnetized material comprising current loops representing the individual dipoles. The equal and opposite currents in adjacent loops cancel each other, leaving a net current along the boundary, called surface bound current.
The surface-bound current density is the current per unit thickness. Substituting the dipole moment in the magnetization expression shows that it equals the surface current. The surface current can be expressed in vector form since it exists only across the boundary.
When the magnetization is non-uniform, currents in adjacent loops no longer cancel. A net volume-bound current develops inside the material. Vectorially, this current equals the curl of the magnetization vector.
The vector potential created by a magnetized material at a field point can be estimated solely from these bound currents and is the sum of the potentials produced by the surface and volume-bound currents.
29.15:
Potential Due to a Magnetized Object
Magnetic dipoles in magnetic materials are aligned when placed under an external magnetic field. For paramagnets and ferromagnets, dipole alignment occurs in the direction of the magnetic field. However, the dipoles align opposite to the field in the case of diamagnets. This state of magnetic polarization due to the external field is called magnetization. Magnetization is defined as the dipole moment per unit volume. It plays a similar role to polarization in electrostatics.
The vector potential due to a single magnetic dipole at a field point is given by,
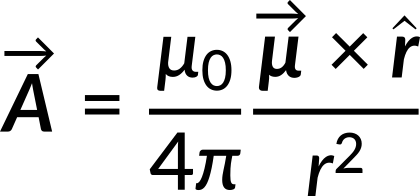
The vector potential can be rewritten in terms of magnetization for a magnetized material with aligned dipole moments.
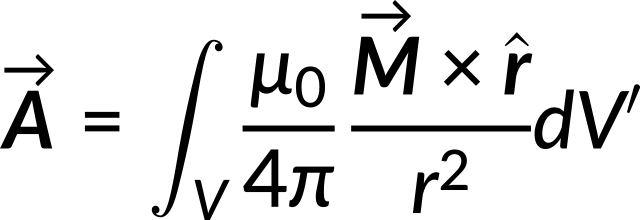
The equation becomes simplified using vector analysis.
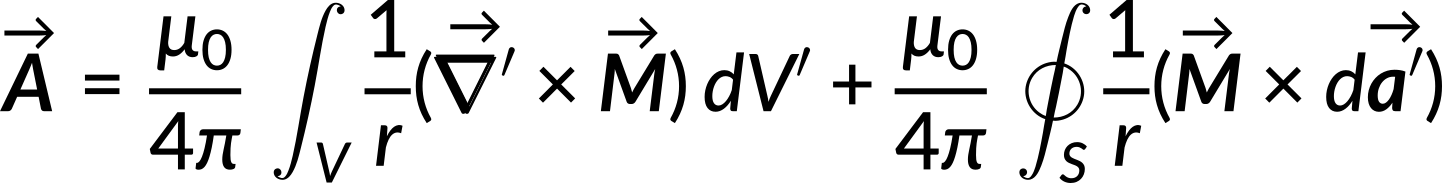
The first term in the above expression is the potential due to the volume current, while the second term is the potential due to the surface current.
Now, the volume current is defined as the curl of the magnetization vector. The surface current is defined as the cross product of the magnetization vector and the unit vector along the area vector. By substituting the expressions for the volume and surface currents, the potential expression reduces to,
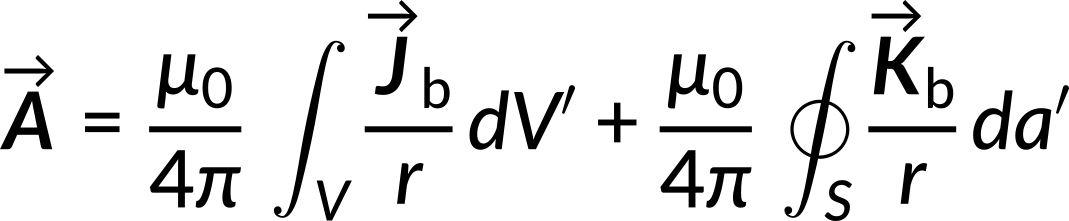
This expression bears an analogy with an electrostatic case, where the field of a polarized object constitutes the field due to bound volume and surface charges.
If the applied magnetic field is uniform, the volume currents become zero, and only the surface current at the boundary of the material exists. When the field applied is non-uniform, the volume currents persist.
Like any steady current, the bound volume current obeys the conservation law. The bound volume current divergence is zero since the divergence of a curl is zero.
Suggested Reading
- David J. Griffiths (2013) Introduction to Electrodynamics, Fourth Edition: Pearson. Pp. 273-279
