29.17:
Ampere’s Law in Matter
The differential form of Ampere's Law in a vacuum correlates the curl of the magnetic field with the current density.
In a magnetized material, the current density is the sum of the free and bound current densities.
The free current arises due to the motion of free electrons within the material, while the bound current arises due to the alignment of magnetic dipole moments.
So, Ampere's Law is modified in a magnetized material to incorporate the bound and free current densities.
The bound volume current density is the curl of the magnetization.
Rearranging the terms involving the curl function, the equation for free current is obtained.
The magnetic field over vacuum permeability minus the magnetization is defined as the magnetic field intensity, H.
So, Ampere's Law in matter states that the curl of H equals the free current density.
In integral form, the line integral of H along an Amperian loop equals the net free current passing through the loop.
The magnetic field intensity in magnetostatics is analogous to the displacement vector in electrostatics.
29.17:
Ampere’s Law in Matter
The total current density in magnetized material is the sum of the free and bound current densities. The free current arises due to the motion of free electrons within the material, while the bound current arises due to the alignment of magnetic dipole moments.
The differential form of Ampere's law in vacuum states that the curl of the magnetic field equals the permeability times the current density. In a magnetized material, the law is modified to incorporate the free and bound current densities.
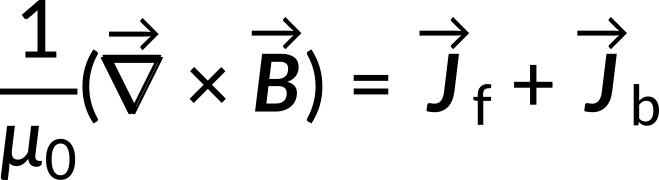
The equation is modified when the bound current density is expressed as the curl of the magnetization vector. The terms involving the curl of the parameters are rearranged as
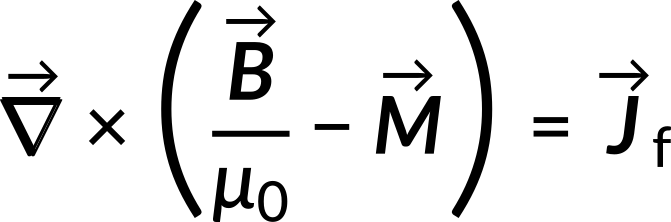
The terms in the bracket can be expressed as magnetic field intensity, 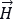 . It is the magnetic field vector upon permeability minus the magnetization vector.
. It is the magnetic field vector upon permeability minus the magnetization vector.
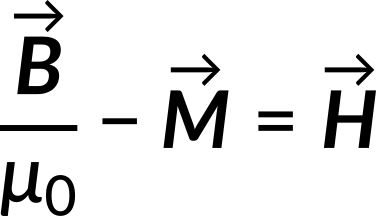
Thus, Ampere's law in matter states that the curl of the 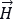 equals the free current density.
equals the free current density.
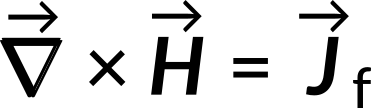
The equation can be written in integral form as
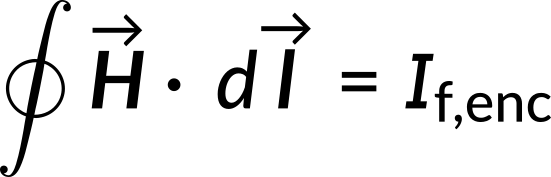
The line integral of 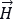 along a closed Amperian loop equals the net free current passing through the loop.
along a closed Amperian loop equals the net free current passing through the loop.
The magnetic field intensity helps express Ampere's law in matter in terms of the free current. Similarly, the electric displacement vector helps in representing Gauss's law in matter in terms of the free charge. Thus, the magnetic field intensity vector in magnetostatics is analogous to the electric displacement vector in electrostatics.
Since an electromagnet is formed when current is passed through a coil, the free current is the known parameter. On the other hand, the B field is a material characteristic. Hence, the H field is often used in experiments rather than the B field.
Suggested Reading
- David J. Griffiths (2013) Introduction to Electrodynamics, Fourth Edition: Pearson. Pp. 279-281
