30.14:
Ampere-Maxwell’s Law: Problem-Solving
A parallel plate capacitor in vacuum is in the charging condition. The radius of each plate is 5 cm. At an instant, the conduction current flowing through the wires is 0.4 A. What will be the displacement current between the plates at this time?
Also, calculate the displacement current density and evaluate the rate of change in the electric field between the plates. Calculate the induced magnetic field between the plates and plot it for a distance of 1–5 cm from the axis.
Displacement current is expressed in terms of electric flux, which in turn, can be obtained in terms of charge.
The displacement current equals the conduction current flowing through the wires, which is 0.4 Amperes.
Furthermore, the displacement current density can be calculated.
As the capacitor charges, the electric field between the plates increases, which is evaluated using displacement current density and the permittivity of free space.
As per the Ampere-Maxwell law, the magnetic field is induced between the capacitor plates, which is calculated for different distances from the axis and plotted as shown.
30.14:
Ampere-Maxwell’s Law: Problem-Solving
A parallel-plate capacitor with capacitance C, whose plates have area A and separation distance d, is connected to a resistor R and a battery of voltage V. The current starts to flow at t = 0. What is the displacement current between the capacitor plates at time t? From the properties of the capacitor, what is the corresponding real current?
To solve the problem, we can use the equations from the analysis of an RC circuit and Maxwell's version of Ampère's law.
For the first part of the problem, the voltage between the plates at time t is given by
Suppose that the z-axis points from the positive plate to the negative plate. In this case, the z-component of the electric field between the plates as a function of time t is given by
Therefore, the z-component of the displacement current Id between the plates of the capacitor can be evaluated as
where the capacitance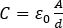 
is being used.
Further, to solve the second part of the above-stated problem, the current into the capacitor after the circuit is closed can be obtained by the charge on the capacitor, which in turn can be evaluated by using the expression for VC. As a result, the real current into the capacitor is found to be the same as the displacement current.
Suggested Reading
- OpenStax. (2019). University Physics Vol. 2. [Web version], pages 94–95. Retrieved from https://openstax.org/books/university-physics-volume-2/pages/16-1-maxwells-equations-and-electromagnetic-waves