31.13:
RLC Circuit as a Damped Oscillator
Consider the differential equation of an RLC circuit. In analogy with the damped harmonic oscillator, the solution of the RLC circuit equation is given by an exponential function.
Differentiating the solution twice with time and substituting the resistance factor and oscillation frequency gives a quadratic equation with two possible solutions.
The sum of these gives the final solution to the RLC circuit equation.
Consider the underdamped case, where the resistance factor is less than the oscillation frequency. In this case, the solution becomes imaginary.
On substituting the imaginary term, the complex solution of the underdamped RLC circuit is obtained. By using Euler's formula, the equation is simplified.
For the equation to be real, A1 and A2 have to be complex conjugates of each other, which further simplifies the solution.
Expressing the coefficients in terms of charge amplitude and substituting the resistance factor, the final solution for the underdamped RLC oscillator is obtained.
Here, ω' and Φ represent the angular frequency and the phase angle of the underdamped RLC circuit, respectively.
31.13:
RLC Circuit as a Damped Oscillator
An RLC circuit combines a resistor, inductor, and capacitor, connected in a series or parallel combination.
Consider a series RLC circuit. Here, the presence of resistance in the circuit leads to energy loss due to joule heating in the resistance. Therefore, the total electromagnetic energy in the circuit is no longer constant and decreases with time. Since the magnitude of charge, current, and potential difference continuously decreases, their oscillations are said to be damped. This is similar to a damped block-spring oscillator, where the amplitude of displacement of the oscillator decreases with time.
The differential equation for damped oscillations in an RLC circuit is given by
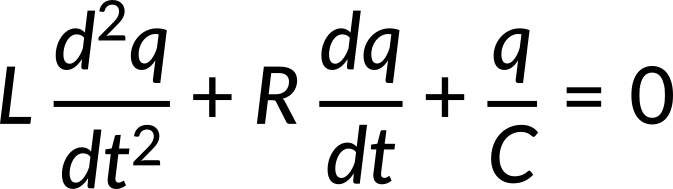
It is known that if the ratio of R/L is less than 1/LC, the circuit becomes an underdamped oscillator. The solution of equation 1 in the case of an underdamped RLC circuit is given by
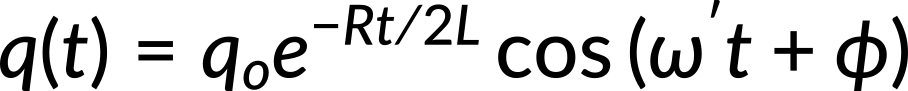
This depicts how the charge on the capacitor oscillates in an underdamped RLC circuit. This solution is the electromagnetic counterpart of the solution for an underdamped spring oscillator that gives the displacement of a damped block-spring oscillator. Analogous to the decrease in displacement amplitude in the block-spring oscillator, the charge oscillates sinusoidally with decreasing amplitude in an underdamped RLC circuit. The angular frequency of the damped oscillations is always less than the angular frequency of the underdamped oscillations.
The energy decay in an underdamped RLC circuit is obtained using the energy relation and is given as
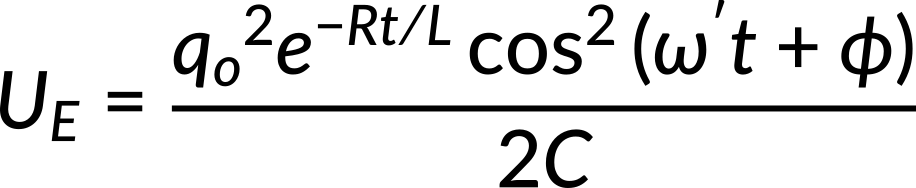
Thus, the energy of the electric field varies sinusoidally, and the amplitude of that oscillation decreases exponentially with time.
Suggested Reading
- Young, H.D. and Freedman, R.A. (2012). University Physics with Modern Physics. San Francisco, CA: Pearson. pp.1010.
- OpenStax. (2019). University Physics Vol. 2. [Web version]. Retrieved from https://openstax.org/books/university-physics-volume-2/pages/14-6-rlc-series-circuits
