Inductance
English
Share
Overview
Source: Yong P. Chen, PhD, Department of Physics & Astronomy, College of Science, Purdue University, West Lafayette, IN
This experiment will use inductive coils to demonstrate the concept of inductor and inductance. Magnetic induction will be demonstrated using a rod magnet inserted into or extracted away from the core of a coil to induce a transient electromotive force (emf) voltage in the coil, measured by a voltmeter. This experiment will also demonstrate the mutual inductance between two coils, where turning on or off a current flowing in a coil can induce an emf voltage in a second coil nearby. Finally, the experiment will demonstrate the self-inductance of a coil, when switching a current off induces an emf to light up a light bulb connected in parallel with the coil.
Principles
According to the Faraday's law, a changing (time-dependent) magnetic field B will induce an electric field, known as the electromotive force (emf) field. If the magnetic field is transverse to a single-loop coil, the emf field will generate an emf voltage V across the two ends of the coil:
 (Equation 1)
(Equation 1)
The magnetic flux through the loop is,

where A is the area of the loop, and if the magnetic field B is along a general direction, B must be replaced with its component perpendicular to the area of the loop, and ΔΦ/Δt is the rate of its change. The minus sign in Equation 1 signifies the direction of the induced emf (or voltage): it always tries to oppose the change of the external B field by generating a current in the coil that produces its own magnetic field in the opposite direction of the change of the B field. The direction of the induced magnetic field is related to the direction of the current in the coil by the red hand rule (wrap the fingers of the right hand around the current direction, the thumb points in the direction of the magnetic field produced by the current). For example, if the external B field is along the +x direction (the area of the loop is in yz plane) and is increasing with time, then the magnetic field generated by the induced emf and current will be in the -x direction; if the external B field is decreasing, the induced emf and current will generate a magnetic field in the +x direction. This is the phenomenon of magnetic induction. For a "solenoid" coil of N turns, the emf voltage generated by each turn will add up to a total emf voltage. During the magnetic induction, the coil can be thought of as an analogue of a battery that would output a voltage and (if some load is connected) a current. In this experiment, this phenomenon will be demonstrated using an increasing or decreasing magnetic field B produced by: (1) a permanent magnet moved toward or away from the coil (Figure 1); (2) another coil with a current I flowing through the coil, where I can be switched on or off (Figure 2); and (3) the coil itself with a current I flowing through, where I can be switched on or off (Figure 3). In the case of (3), the induction is referred as self-induction (and the solenoid is an example of an "inductor"). For both cases (2) and (3), since the magnetic flux or magnetic field (whose change causes the induction) is proportional to the current I, the induced emf voltage is proportional to the rate of the change of the current (ΔI/Δt), with the proportional factor L known as the mutual inductance as in case (2) or self-inductance as in case (3), respectively:
 (Equation 2)
(Equation 2)
The direction of the voltage V is determined in a similar manner as described above: the emf V will try to produce a current I, and its own magnetic field that opposes the change in the original magnetic field B.
Procedure
1. Magnetic Induction
- Obtain a solenoid coil (with a hollow core) and a rod magnet (with its North and South poles labeled).
- Obtain an analogue bipolar ammeter with an indicator needle. The needle is nominally at the middle position at zero reading, and will deflect to the right or left depending on the direction of current flow (positive reading means the current flows from the positive terminal to and negative terminal inside the ammeter).
- Connect the two ends of the solenoid to the "+" and "−" terminals of the ammeter, as in Figure 1. The connection can be made with cables with clamps or banana plugs into receiving ports on the instruments.
- Bring the rod magnet closer to the coil and insert its north end into its core, as shown in Figure 1. Observe the ammeter and record the sign of its reading. For all observations to be conducted in the following, always record both the sign and the approximate magnitude of the reading.
- Extract the magnet back out of the coil, and observe the reading on the ammeter.
- With the rod magnet far away from the coil, flip it over and now move the South end closer to the coil. Insert the South end into the core of the coil, and observe the reading on the ammeter.
- Extract the magnet back out of the coil again, and observe the reading on the ammeter.
- Repeat steps 1.6 and 1.7 above again (insert and extract South pole of the magnet) but with a slower and then a faster speed, and observe and compare the reading on the ammeter.
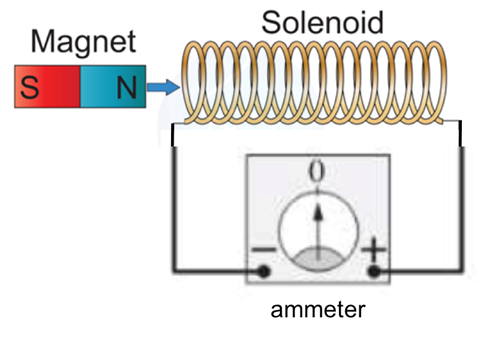
Figure 1: Diagram showing a magnet moving toward/away from a coil to induce a current in the coil (magnetic induction).
2. Mutual Inductance
- Obtain a second solenoid coil (referred to as coil #2), and bring it close to the first coil (referred as coil #1) as shown in Figure 2. The two coils are aligned approximately along a common axis.
- Connect the two ends of coil #2 to a DC voltage source with a switch, as shown in Figure 2. Coil #1 is still connected to the analogue ammeter.
- With the switch open, set the voltage source to +2 V, then close the switch to allow a current to flow in the coil #2, and observe the reading on the ammeter connected to coil #1 when the switch is turned on.
- Now open the switch, and observe the reading on the ammeter.
- Set the voltage source to −2 V (or alternatively, swap the two wires connected to the plus and minus terminals of the voltage source to reverse the sign of the voltage and current to be applied to coil #1), repeat steps 2.3 (switch on) and 2.4 (switch off), and observe the ammeter connected to coil #1.
- Now insert coil #2 into the core of coil #1 as fully as possible, repeat the above step 2.5, and observe the reading on the ammeter connected to coil #1.

Figure 2: Diagram showing that a current switching on or off in a coil would induce current in another nearby coil (mutual induction).
3. Self-inductance
- Obtain a light bulb and connect it in series with the ammeter, then connect the combination to coil #2 in parallel with the volt supply, as shown in Figure 3. The voltage on the volt supply is set to be 1 V.
- Close the switch to let the current flow through the coil. The light bulb should be dim because the coil has a much smaller resistance than the light bulb, and most of the current will flow through the coil.
- Open the switch so that the volt supply is disconnected from the rest of the circuit, and observe the light bulb and the ammeter reading when the switch is just opened.

Figure 3: Diagram showing a circuit to demonstrate self-induction, where tuning off current in a coil induces a transient voltage and current in a light bulb connected to it.
Inductors — typically in the form of coils — are commonly used in many circuit applications. Their purpose is to store magnetic energy when a steady state current flows.
In a loop that forms a closed circuit, the changing magnetic field induces an electromotive force that drives the current. This phenomenon is called electromagnetic induction. An inductor is simply a coil of wire and it has the property of self-inductance, which relates the voltage across its terminals with the change in its own magnetic field.
This video will illustrate the concepts behind inductance and then demonstrate an induction experiment using a bar magnet and a coil. Lastly, we will review some of the current applications for inductors.
Magnetic flux may be thought of as the amount of magnetic field passing through an area. For a uniform magnetic field B perpendicular to an area A, magnetic flux phi is simply the product of the two. According to Faraday's law of induction, a changing magnetic flux in a loop of wire generates an electromotive force, or EMF, along the loop. This EMF is equal to the negative of the rate of change of magnetic flux over time.
The magnetic flux's rate of change determines the polarity of the induced electromotive force. The negative sign in the expression for Faraday's law means that if the magnetic field decreases with time, the EMF is positive. If it increases with time, the EMF is negative. When the loop is a closed circuit, the induced EMF drives current that in turn generates its own magnetic field. This magnetic field has an orientation given by the Right Hand Rule. If the fingers of the right hand curl around the direction of current in the loop, then the thumb of the right hand would point in the direction of the generated magnetic field. The induced current must flow in the direction that creates a magnetic field opposing the external magnetic field's rate of change.
For example, the magnetic field from this magnet points upward through a single loop of wire. Moving the magnet away from the loop decreases the magnetic field strength through the loop. The change in magnetic flux- represented by a vector pointing downward-induces a positive EMF that drives current counterclockwise as shown. By the Right Hand Rule, the current creates a magnetic field that points up within the loop to oppose the decreasing magnetic field or flux. In contrast, moving the magnet toward the loop increases the magnetic field there. The change in magnetic flux is represented by a vector pointing upward. In this case it induces a negative EMF that drives current clockwise. By the Right Hand Rule, current in this direction creates a magnetic field that points down within the loop to oppose the increasing magnetic field or flux.
Now let's move on from a loop to a solenoid, which is simply multiple loops of wire wound around a core of air or magnetic material. It is a commonly used inductor in electrical circuits. If current flows through a solenoid, it creates a magnetic field within the inductor. The direction of this magnetic field is given by the right hand rule. This field in turn produces a magnetic flux in the direction same as that of the field, and the amount of this flux is proportional to the current. Therefore, if the current changes with time, so does the magnetic flux. Following the Faraday's law, the changing flux induces a voltage that drives current through the coil such that the induced current's magnetic field opposes the change in the original flux. This phenomenon of voltage induction across its own terminals in response to varying current is called self-induction, and the total induced voltage across the solenoid is the number of turns N, multiplied by the EMF of a single loop.
Now that we've explained the basics, let's see how to study electromagnetic induction in a physics lab.
All of the following experiments use an analog bipolar ammeter, which has a needle that deflects to the right or left of the zero point, depending on the direction of current flow.
First, obtain a solenoid with a hollow core, a rod magnet with clearly labeled north and south poles, and the analog bipolar ammeter. Then connect the solenoid to the ammeter. For the first trial, insert the north pole of the magnet into the end of the solenoid connected to the negative terminal of the ammeter. Observe the ammeter and record the polarity and approximate magnitude of the needle's deflection. Pull the magnet out of the solenoid and record the polarity and approximate magnitude of the ammeter needle's deflection.
Now turn the magnet around and insert and remove the south pole from the end of the solenoid connected to the negative terminal of the ammeter. Repeat this experiment by inserting the south pole of the magnet into the coil and then removing it-first more slowly and then more quickly than in the first trial. When the north pole moves near and enters the solenoid, it induces current that causes a momentary positive deflection of the ammeter. When the north pole is removed from the solenoid, the deflection is negative. Reversing the orientation of the magnet also reverses the ammeter response.
Finally, the speed of movement affects the change of magnetic field with time, which determines the induced voltage and current. Slower motion induces less current and a smaller reading, and faster motion induces more current and a larger reading.
For the self-inductance experiment, connect a light bulb, inductor coil, voltage supply set at positive one volt, switch, and the analog ammeter as shown. Assemble the circuit with the switch open so no current flows.
Close the switch to connect the voltage source to both the light bulb and inductor coil. Observe the bulb, which appears to be dimly lit. Open the switch to disconnect the voltage supply from the circuit. Observe the light bulb and the ammeter at the moment the switch is opened then record the result. The light bulb brightens briefly and the ammeter shows a positive reading at the same time. This happens due to self-induction and several events take place during this brief period of time.
Initially, when the switch is closed, current flow through both the coil and light bulb, but much more current flows through the coil compared to the light bulb, since the coil has lower resistance compared to the bulb. Opening the switch disconnects the voltage source. This causes the current through the inductor to decrease.
This changing current through the inductor causes a change in its magnetic flux, which in turn induces a transient current that opposes the decrease by flowing in the same direction as the original current. The combination of the two – original and transient current — yields the total inductor current, which now flows through the bulb and lights it up briefly, and at the same time causes a deflection in the ammeter to indicate a positive current.
Electromagnetic induction has many applications in modern devices, and is a fundamental method of transferring energy and information without physical contact.
Induction is the core principle behind the functioning of devices called transformers. A transformer has a pair of input terminals connected to a primary winding-or coil-and a pair of output terminals connected to a secondary winding. A core consisting of steel, ferrite or even simply air, magnetically couples the two windings. A voltage across one winding causes current to flow through it, creating a magnetic field. Magnetic flux, or the density of the magnetic field, is then coupled to the secondary winding through the core, where it induces a voltage. This principle is called mutual induction.
Another application of inductors is AC induction motors, which are the workhorses of modern industry due to their simplicity, ruggedness, and reliability. An induction motor has only two main parts. The first is the stationary part, called the stator, which consists of stationary coils around a cavity. Suspended in the cavity is the rotor, which is a pair of end rings capping a cylindrical arrangement of bars. A three-phase AC induction motor uses three-phase power, with each phase connected to its own, separate set of stator coils. The coils are arranged in a pattern that generates one magnetic field for each phase of the supplied power. The resulting net magnetic field, called the "stator magnetic field" rotates with constant velocity.
The rotating magnetic flux induces current in the rotor, similar to the way that a transformer transfers power from the primary coil to the secondary. The current through the bars of the rotor in turn creates its own magnetic field, called the "induced rotor magnetic field." The interaction between these two fields produces a force on the rotor, which causes it to follow the stator magnetic field, like an iron bar following the magnets around it.
You've just watched JoVE's introduction to electromagnetic inductance. You should now understand how a time varying magnetic field induces an electromotive force in a conductor, and how the resulting current produces its own magnetic field. Thanks for watching!
Results
Representative results for what may be observed on the ammeter reading for Sections 1 and 2 (setups in Figures 1 and 2) are summarized in Tables 1 and 2 below.
| Procedure Step | Orientation of Rod Magnet | Motion of Magnet | Reading on the ammeter |
| 1.4 | South-North (North is at the right end of rod, as in Figure 1) | Moving toward coil (left end) | Positive |
| 1.5 | South-North | Moving away from the coil | Negative |
| 1.6 | North-South | Moving toward coil | Negative |
| 1.7 | North-South | Moving away from the coil | Positive |
Table 1: Representative results for Section 1. For step 1.8, observe that a faster speed of motion gives a larger reading (larger needle deflection) on the ammeter.
| Procedure Step | Volt Supply Setting | Switch action | Reading on the ammeter |
| 2.3 | +2 V | Turning on | Positive |
| 2.4 | +2 V | Turning off | Negative |
| 2.5 | −2 V | Turning on | Negative |
| 2.5 | −2 V | Turning off | Positive |
Table 2: Representative results for Section 2. For step 2.6, observe that placing coil #2 inside coil #1 gives a larger reading (while the signs of the reading remain the same) on the ammeter compared to step 2.5 for each corresponding switch action.
For Section 3, if initially the current due to the volt supply (+1 V) is flowing from the right to the left in the coil, turning it off (opening the switch) will induce a transient current along the same direction. The light bulb will light up briefly, and the ammeter will register a positive reading for the connection given in Figure 3.
Applications and Summary
In this experiment, we have demonstrated how changing a magnetic field (by moving a magnet) induces a current in a coil, and also how changing the current in the coil induces current in another coil (mutual induction). We also demonstrated that changing the current in a coil induces a voltage and current in the same coil (self-induction).
Inductors (typically in the form of coils) are commonly used in many circuit applications, such as to store magnetic energy when a steady state current flows. They are useful for electrical signal processing; for example, taking the derivative or integral of an electrical signal, for filtering, and for resonance circuits. They are also used in transformers to change the voltage of AC signals.
The author of the experiment acknowledges the assistance of Gary Hudson for material preparation and Chuanhsun Li for demonstrating the steps in the video.
Transcript
Inductors — typically in the form of coils — are commonly used in many circuit applications. Their purpose is to store magnetic energy when a steady state current flows.
In a loop that forms a closed circuit, the changing magnetic field induces an electromotive force that drives the current. This phenomenon is called electromagnetic induction. An inductor is simply a coil of wire and it has the property of self-inductance, which relates the voltage across its terminals with the change in its own magnetic field.
This video will illustrate the concepts behind inductance and then demonstrate an induction experiment using a bar magnet and a coil. Lastly, we will review some of the current applications for inductors.
Magnetic flux may be thought of as the amount of magnetic field passing through an area. For a uniform magnetic field B perpendicular to an area A, magnetic flux phi is simply the product of the two. According to Faraday’s law of induction, a changing magnetic flux in a loop of wire generates an electromotive force, or EMF, along the loop. This EMF is equal to the negative of the rate of change of magnetic flux over time.
The magnetic flux’s rate of change determines the polarity of the induced electromotive force. The negative sign in the expression for Faraday’s law means that if the magnetic field decreases with time, the EMF is positive. If it increases with time, the EMF is negative. When the loop is a closed circuit, the induced EMF drives current that in turn generates its own magnetic field. This magnetic field has an orientation given by the Right Hand Rule. If the fingers of the right hand curl around the direction of current in the loop, then the thumb of the right hand would point in the direction of the generated magnetic field. The induced current must flow in the direction that creates a magnetic field opposing the external magnetic field’s rate of change.
For example, the magnetic field from this magnet points upward through a single loop of wire. Moving the magnet away from the loop decreases the magnetic field strength through the loop. The change in magnetic flux- represented by a vector pointing downward-induces a positive EMF that drives current counterclockwise as shown. By the Right Hand Rule, the current creates a magnetic field that points up within the loop to oppose the decreasing magnetic field or flux. In contrast, moving the magnet toward the loop increases the magnetic field there. The change in magnetic flux is represented by a vector pointing upward. In this case it induces a negative EMF that drives current clockwise. By the Right Hand Rule, current in this direction creates a magnetic field that points down within the loop to oppose the increasing magnetic field or flux.
Now let’s move on from a loop to a solenoid, which is simply multiple loops of wire wound around a core of air or magnetic material. It is a commonly used inductor in electrical circuits. If current flows through a solenoid, it creates a magnetic field within the inductor. The direction of this magnetic field is given by the right hand rule. This field in turn produces a magnetic flux in the direction same as that of the field, and the amount of this flux is proportional to the current. Therefore, if the current changes with time, so does the magnetic flux. Following the Faraday’s law, the changing flux induces a voltage that drives current through the coil such that the induced current’s magnetic field opposes the change in the original flux. This phenomenon of voltage induction across its own terminals in response to varying current is called self-induction, and the total induced voltage across the solenoid is the number of turns N, multiplied by the EMF of a single loop.
Now that we’ve explained the basics, let’s see how to study electromagnetic induction in a physics lab.
All of the following experiments use an analog bipolar ammeter, which has a needle that deflects to the right or left of the zero point, depending on the direction of current flow.
First, obtain a solenoid with a hollow core, a rod magnet with clearly labeled north and south poles, and the analog bipolar ammeter. Then connect the solenoid to the ammeter. For the first trial, insert the north pole of the magnet into the end of the solenoid connected to the negative terminal of the ammeter. Observe the ammeter and record the polarity and approximate magnitude of the needle’s deflection. Pull the magnet out of the solenoid and record the polarity and approximate magnitude of the ammeter needle’s deflection.
Now turn the magnet around and insert and remove the south pole from the end of the solenoid connected to the negative terminal of the ammeter. Repeat this experiment by inserting the south pole of the magnet into the coil and then removing it-first more slowly and then more quickly than in the first trial. When the north pole moves near and enters the solenoid, it induces current that causes a momentary positive deflection of the ammeter. When the north pole is removed from the solenoid, the deflection is negative. Reversing the orientation of the magnet also reverses the ammeter response.
Finally, the speed of movement affects the change of magnetic field with time, which determines the induced voltage and current. Slower motion induces less current and a smaller reading, and faster motion induces more current and a larger reading.
For the self-inductance experiment, connect a light bulb, inductor coil, voltage supply set at positive one volt, switch, and the analog ammeter as shown. Assemble the circuit with the switch open so no current flows.
Close the switch to connect the voltage source to both the light bulb and inductor coil. Observe the bulb, which appears to be dimly lit. Open the switch to disconnect the voltage supply from the circuit. Observe the light bulb and the ammeter at the moment the switch is opened then record the result. The light bulb brightens briefly and the ammeter shows a positive reading at the same time. This happens due to self-induction and several events take place during this brief period of time.
Initially, when the switch is closed, current flow through both the coil and light bulb, but much more current flows through the coil compared to the light bulb, since the coil has lower resistance compared to the bulb. Opening the switch disconnects the voltage source. This causes the current through the inductor to decrease.
This changing current through the inductor causes a change in its magnetic flux, which in turn induces a transient current that opposes the decrease by flowing in the same direction as the original current. The combination of the two – original and transient current — yields the total inductor current, which now flows through the bulb and lights it up briefly, and at the same time causes a deflection in the ammeter to indicate a positive current.
Electromagnetic induction has many applications in modern devices, and is a fundamental method of transferring energy and information without physical contact.
Induction is the core principle behind the functioning of devices called transformers. A transformer has a pair of input terminals connected to a primary winding-or coil-and a pair of output terminals connected to a secondary winding. A core consisting of steel, ferrite or even simply air, magnetically couples the two windings. A voltage across one winding causes current to flow through it, creating a magnetic field. Magnetic flux, or the density of the magnetic field, is then coupled to the secondary winding through the core, where it induces a voltage. This principle is called mutual induction.
Another application of inductors is AC induction motors, which are the workhorses of modern industry due to their simplicity, ruggedness, and reliability. An induction motor has only two main parts. The first is the stationary part, called the stator, which consists of stationary coils around a cavity. Suspended in the cavity is the rotor, which is a pair of end rings capping a cylindrical arrangement of bars. A three-phase AC induction motor uses three-phase power, with each phase connected to its own, separate set of stator coils. The coils are arranged in a pattern that generates one magnetic field for each phase of the supplied power. The resulting net magnetic field, called the “stator magnetic field” rotates with constant velocity.
The rotating magnetic flux induces current in the rotor, similar to the way that a transformer transfers power from the primary coil to the secondary. The current through the bars of the rotor in turn creates its own magnetic field, called the “induced rotor magnetic field.” The interaction between these two fields produces a force on the rotor, which causes it to follow the stator magnetic field, like an iron bar following the magnets around it.
You’ve just watched JoVE’s introduction to electromagnetic inductance. You should now understand how a time varying magnetic field induces an electromotive force in a conductor, and how the resulting current produces its own magnetic field. Thanks for watching!
