26.10: Continuity Equation
The total amount of current flowing per unit cross-sectional area is called the current density. Hence, the current passing through a cross-sectional area can be written as the surface integral of the current density.
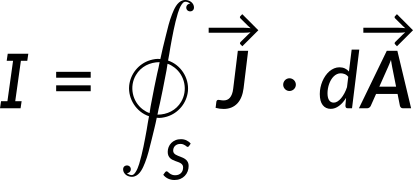
According to the conservation of charge, the total current flowing out of a given volume equals the rate of decrease of charge within that volume.
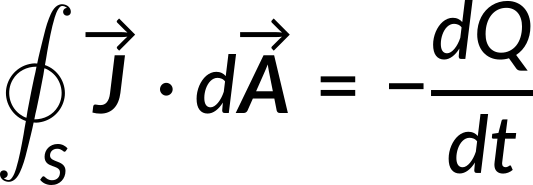
Now, the total charge can be written in terms of the volume charge density.
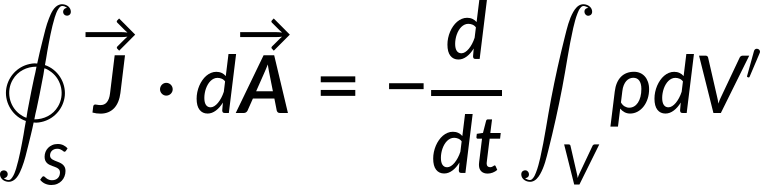
The charge density is a space function. Hence, applying the Leibniz rule, the time derivative can be moved inside the integral.
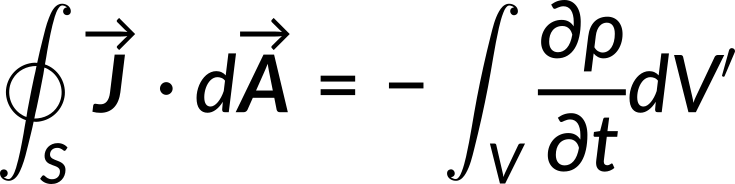
When the divergence theorem is applied to the left-hand side of the above equation, the closed surface integral is converted into the volume integral.
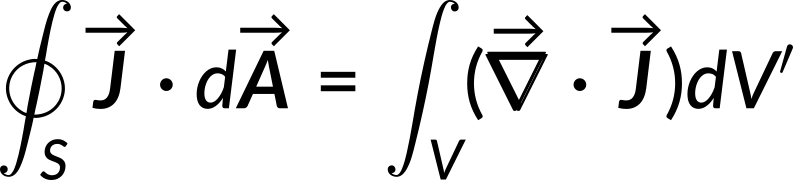
Since this relation holds for any volume, the integrands are equal and the obtained relation is called the continuity equation. This states that the divergence of the current density equals the negative rate of change of volume charge density.
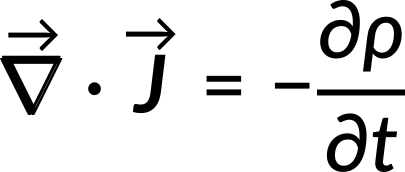
For steady currents, the charge density is invariant with time. Hence, the divergence of the current density is zero.


