19.7: Distribution of Molecular Speeds
The motion of molecules in a gas is random in magnitude and direction for individual molecules, but a gas of many molecules has a predictable distribution of molecular speeds. This predictable distribution of molecular speeds is known as the Maxwell-Boltzmann distribution. The distribution of molecular speeds in liquids is comparable to that of gases but not identical and can help to understand the phenomenon of the boiling and vapor pressure of a liquid. Consider that a molecule requires a speed equal to or more than at va to escape from the surface of a liquid into the adjacent vapor, as shown in Figure 1.
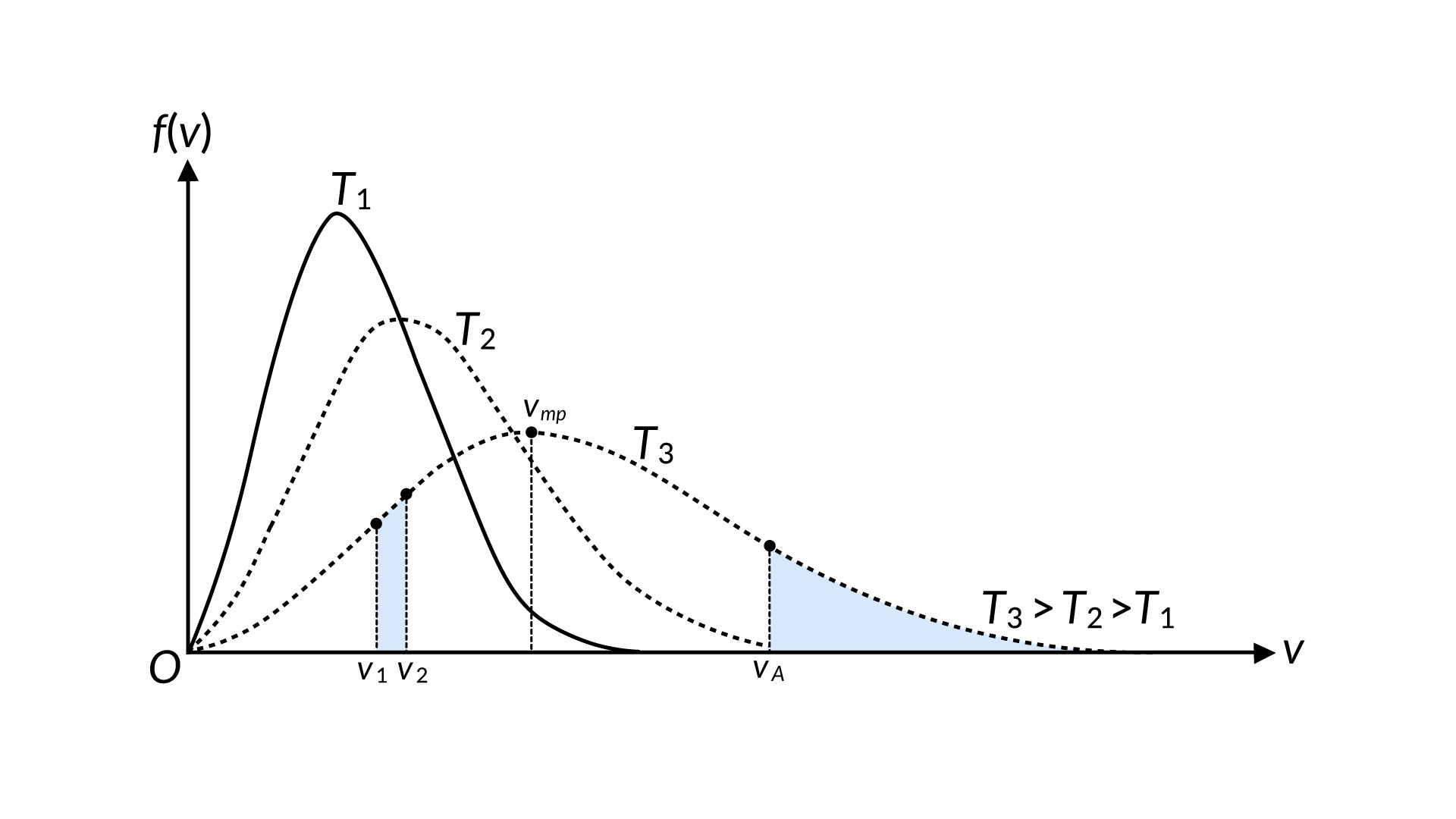
The number of similar molecules, represented by the area under the curve, increases swiftly with temperature. Thus, the rate at which molecules can escape is highly temperature-dependent. To counter this process, the molecules in the vapor phase collide inelastically with the surface and get trapped back in the liquid phase. The number of molecules that experience this situation per unit time is related to the vapor phase pressure. When these two processes proceed at the same rate, phase equilibrium is established between liquid and gas. So, if the molecular speed distributions are known for various temperatures, we can make a theoretical prediction of vapor pressure as a function of temperature. Rates of chemical reactions are often strongly temperature-dependent, and the reason for this is contained in the Maxwell-Boltzmann distribution.


