4.1:
反应化学计量
A subscription to JoVE is required to view this content. Sign in or start your free trial.
JoVE Core
Chemistry
Reaction Stoichiometry
考虑一个平衡的化学反应,比如氢气的燃烧。这里,反应物和产物之间 的定量关系—H_2、O_2 和 H_2O—是指 2 个 H_2 分子与 1 个 O_2 分子反应生成 2 个 H_2O 分子。这种定量关系被称为化学计量学,它和任何配方都很相似。假设用 2 片意大利腊肠、1 片奶酪 和 2 片意大利面包做一个三明治。为了做三个三明治,配料的数量是原来的三倍。用 10 片意大利腊肠可以做多少个三明治?因为意大利腊肠和三明治的比例是 2:1,所以可以做 5 个三明治。同样的过程也适用于化学反应。例如,考虑一下氨气的合成。化学计量系数直接 表示分子的相对数量,相当于以摩尔为单位的相对数量。一摩尔的氮气和三摩尔的氢气 反应生成两摩尔的氨气。要制造四摩尔的氨气,反应物的量 要加倍。氮气与氨气的摩尔比为 1:2,而氢气与氨气的摩尔比为 3:2。如果有 15 摩尔的氢气,可以合成多少摩尔的氨气?利用摩尔比作为转换因子,可以合成 10 摩尔的氨气。为了从产物的质量来估计 反应物的质量,或者反过来,需要遵循一个途径。与摩尔转换不同,涉及质量的计算 不是直接的。首先,已知的质量被转换成摩尔数。然后,应用摩尔比。最后,使用相关化合物的摩尔质量 将以摩尔为单位的量转换为质量。例如,考虑一下碳氢火箭推进剂 的燃烧—也就是它与氧气的反应。每 5000 克的燃料大约需要 多少克的液氧?首先,用燃料的近似摩尔质量 将 5000 克转换成摩尔数。然后,用 35:2 的摩尔比 来计算所需的 分子氧的摩尔数。最后,利用分子氧的摩尔质量 来确定航天器上每 5000 克的燃料 需要在舱内储存大约 17000 克的 氧气。
4.1:
反应化学计量
一个平衡的化学方程式以非常简洁的格式提供了大量信息。化学式提供了涉及化学变化的反应物和产物的身份,从而可以对反应进行分类。系数提供了这些化学种类的相对数量,从而可以定量评估反应所消耗和产生的物质量之间的关系。这些定量关系称为反应的化学计量,该术语源自希腊语 stoicheion (意思是“元素”)和 metron (意思是“度量”) ;)。
反应的化学计量可帮助预测需要多少反应物才能生成所需量的产物,或者在某些情况下,由特定量的反应物会形成多少产物。
化学计量系数
化学方程式的系数表示每种物质的摩尔数。例如,考虑氮气和氢气反应生成氨。化学计量学表明,一摩尔的氮与三摩尔的氢反应生成两摩尔的氨。

由于一个摩尔包含's阿伏伽德罗分子数,所以分子的相对数与摩尔的相对数相同。读该方程式的另一种方法是“一个氮分子和三个氢分子反应生成两个氨分子。
化学计量因素
平衡化学方程式用于确定与给定量的另一种反应物反应或产生给定量的产物所需的一种反应物的量,等等。平衡方程式中的系数用于导出允许计算所需数量的化学计量因子。在氢和氮的反应中,由氢分子以2:3的比例产生氨分子。这意味着三摩尔的氢在化学计量上相当于两摩尔的氨。基于此,得出以下化学计量因素:
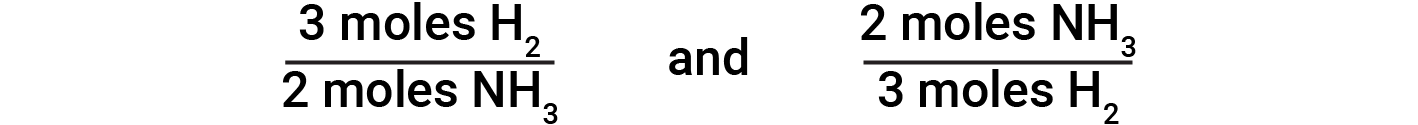
分子到分子的转换
对于由氮和氢形成氨的平衡化学反应,N 2 和NH 3 之间的以下化学计量摩尔比为1:2。然后,通过将氮的摩尔量乘以与两种感兴趣的物质有关的化学计量转换因子,得出氨的摩尔量。

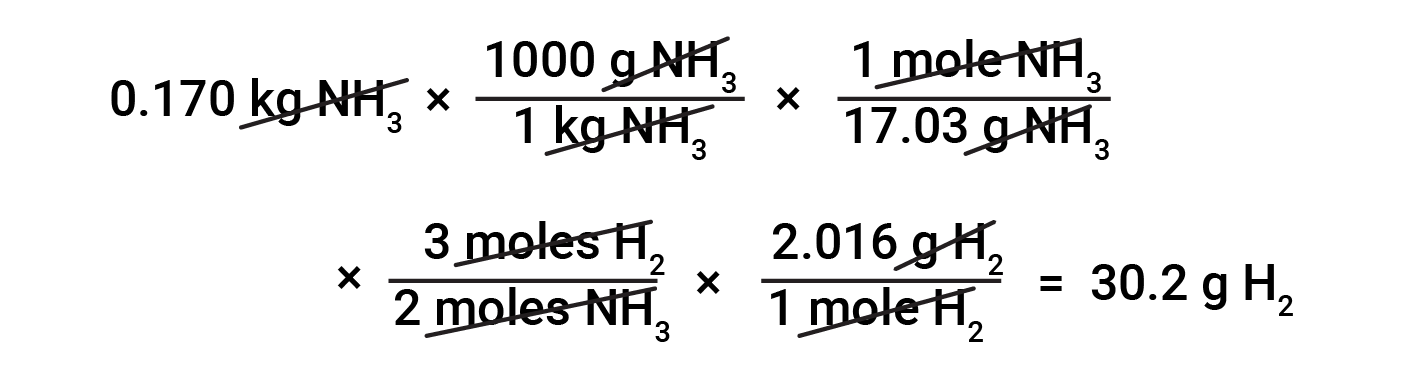
质量到质量的转换
基于化学计量的物质质量转换需要了解摩尔比和摩尔质量。例如,为了找到产生0.170千克氨所需的氢质量,首先,使用氨的摩尔质量将氨的质量转换为氨的量(以摩尔计)。然后,来自平衡方程式的合适的化学计量因子将氨的量(以摩尔计)转换为氢的量(以摩尔计)。最后,氢的摩尔质量将氢的量(以摩尔计)转换为氢的质量。
本文改编自 OpenStax 化学2e,第4.3节:反应化学计量。
