14.4:
Gravity between Spherical Bodies
An apple released from a tree naturally tends to fall on the ground. This downward force was thought to be unique to the Earth.
However, Sir Isaac Newton reasoned that this force also causes the Moon to follow its path around the Earth.
Assuming that the Earth and the Moon have spherically symmetric mass distributions, their masses can be considered to be concentrated at their respective centers.
The Earth's mass is 5.97 × 1024 kilograms, and the Moon's mass is 7.35 × 1022 kilograms. The average distance between their centers is 3.84 × 108 meters.
Recall that the gravitational constant equals 6.67 × 10−11 newton meter squared per kilogram squared.
Substituting the known values in the gravitational force equation, the gravitational force between the Earth and the Moon is estimated to be 1.98 × 1020 newtons.
Similarly, considering the Sun as a spherically symmetric body, substituting its mass and its distance from the Earth, the gravitational force between the Sun and the Earth can be calculated.
14.4:
Gravity between Spherical Bodies
Newton's law of gravitation describes the gravitational force between any two point masses. However, for extended spherical objects like the Earth, the Moon, and other planets, the law holds with an assumption that masses of spherical objects are concentrated at their respective centers.
This assumption can be proved easily by showing that the expression for gravitational potential energy between a hollow sphere of mass (M) and a point mass (m) is the same as it would be for a pair of extended spherical solid objects.
Consider a tiny ring of width Rdϕ and mass dM on the surface of a spherical hollow sphere at a distance s from the point mass as shown in Figure 1(a).
The gravitational potential energy between the ring and the point mass (m) is expressed as:
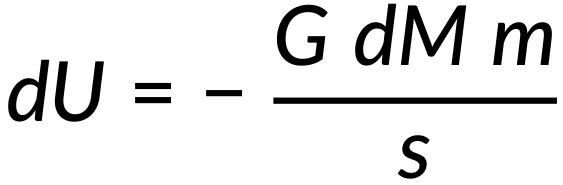
The ratio of the ring's mass to the entire shell's mass is equal to the ratio of the ring's area to the shell's area. Therefore, on simplification, the ring's mass can be expressed as:
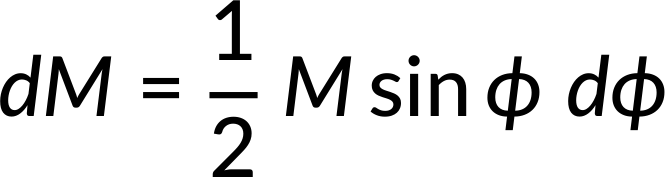
Now, the square of distance (s) can be expressed as the sum of squares of the triangle's other two sides, as seen in Figure 1(b).
Simplifying further and taking differentials on either side,

Considering the entire shell, s can vary between r − R and r + R, as seen in Figure 1(c).
Therefore, substituting dM and s in the potential energy equation and integrating within the limits of r − R to r + R, the relation obtained is the potential energy between point masses m and M at a distance r.
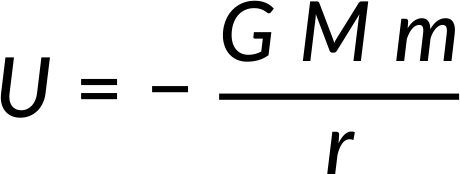
Therefore, the assumption is proven.
Since force is a derivative of potential energy, the assumption holds for gravitational forces between two spherically solid objects like the Earth and the Moon. Therefore, Newton's law of gravitation can be used to determine the gravitational force between the Earth and the Moon, and the Earth and the Sun.
