14.3:
Gravitation Between Spherically Symmetric Masses
The gravitational potential energy between two spherically symmetric objects is given by the objects' masses and the distance between them, assuming that the mass is concentrated at the center.
Consider a point mass placed at a distance from a spherical shell. The spherically symmetric mass distribution comprises multiple concentric shells, and all the particles in a specific ring are at equal distances from the point mass.
The potential between the ring and the point mass can be obtained when the ring's mass is known. The ratio between the ring's area and the shell's area equals the ratio of their masses.
Solving the relationship between the distances, applying it, and integrating the expression gives the potential between the shell and the point mass. This expression is the same as the potential between two point masses.
If the point mass is inside the shell, then the gravitational potential is the same everywhere for all the points inside the cavity.
As the force is a derivative of the potential, the assumption also holds for gravitational force.
14.3:
Gravitation Between Spherically Symmetric Masses
The gravitational potential energy between two spherically symmetric bodies can be calculated from the masses and the distance between the bodies, assuming that the center of mass is concentrated at the respective centers of the bodies.
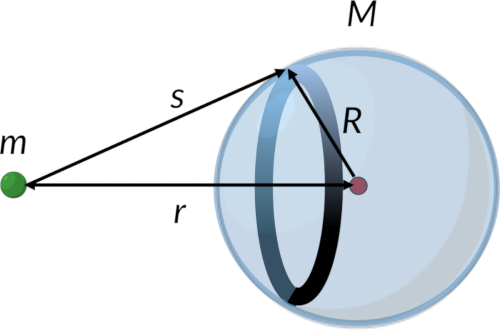
Consider that a spherically symmetric mass distribution comprises multiple concentric spherical shells. A point mass is placed at a distance 'r' from the center of mass of the spherical shell. All the particles in a given spherical ring on the surface of the shell are at equal distances from the point mass.
The potential between the point mass and the ring can be obtained from the ring's mass. Integrating the expression for the potential energy between a point mass and a ring over the limits of distance gives the gravitational potential energy, which is the same as the potential energy between two point masses.
If the point mass is inside the shell, then the limits of integration change. This shows that the potential energy does not depend on the distance and is the same everywhere for all points inside the shell. However, no work is done on the point mass if it is inside the shell.
Suggested Reading
- Young, H.D. and Freedman, R.A. (2012). University Physics with Modern Physics. San Francisco, CA: Pearson. pp. 418-420.
- Verma, H.C. (2008). Concepts of Physics Part I, Fourth Edition. pp. 207–209.
