15.1:
Simple Harmonic Motion
If moving objects repeat their path over a regular interval, it is called harmonic or periodic motion. Periodic motion in which an object moves to and fro from a fixed point is called oscillation.
If the restoring force on the object is proportional to the displacement from the equilibrium position, the oscillation is called simple harmonic motion. However, not all periodic oscillations are simple harmonic motions.
Consider a ruler with one end fixed to the tabletop and the other free with a mass attached. When this system is pulled up and released, it vibrates.
Here, the acceleration is directed toward the center of oscillation and is proportional to the displacement from the equilibrium position. As a result, the force is proportional to the displacement but in the opposite direction. The proportionality constant is the spring constant.
One complete oscillation is called a cycle, and the time required to complete one cycle is called a period. The number of cycles per unit time is the frequency.
At equilibrium, the net force is zero. The maximum displacement from the equilibrium position is the amplitude.
15.1:
Simple Harmonic Motion
Simple harmonic motion is the name given to oscillatory motion for a system where the net force can be described by Hooke's law. If the net force can be described by Hooke's law and there is no damping (by friction or other non-conservative forces), then a simple harmonic oscillator will oscillate with equal displacement on either side of the equilibrium position. To derive an equation for period and frequency, the equation of motion is used. The period of a simple harmonic oscillator is given by

and, because the frequency and period have inverse relation, the frequency of a simple harmonic oscillator is
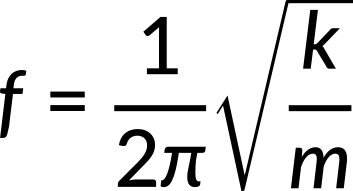
Note that neither period nor frequency has any dependence on amplitude, and the SI unit for frequency is Hertz.
Now, consider one example of each. (a) A medical imaging device produces ultrasound by oscillating with a period of 0.400 μs. What is the frequency of this oscillation? (b) The frequency of middle C on a typical musical instrument is 264 Hz. What is the time for one complete oscillation?
Both can be answered using the inverse relationship between period and frequency. Substituting the given value of period in the frequency expression, the frequency of oscillation is found.
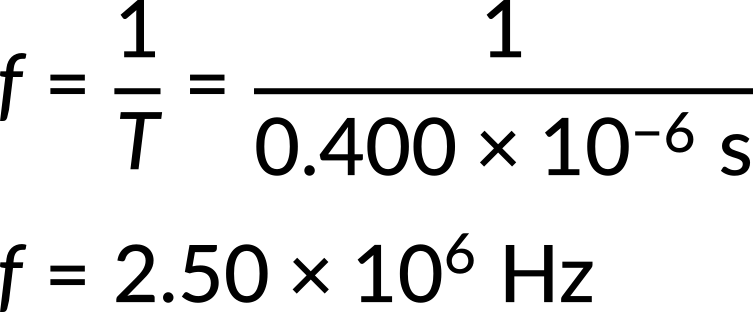
Substituting the given value for the frequency into the time period expression, the time for one complete oscillation is obtained.
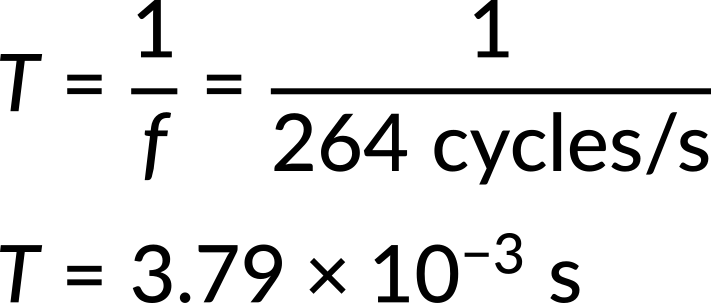
Suggested Reading
- OpenStax. (2019). University Physics Vol. 1. [Web version]. Retrieved from (Pg. No. 744-745) https://openstax.org/books/university-physics-volume-1/pages/1-introduction
- OpenStax. (2020). College Physics [Web version]. (Pg. No. 671-674) https://openstax.org/details/books/college-physics
