19.7:
Distribution of Molecular Speeds
Consider a gas in a container, where all gas molecules have kinetic energy, a function of the molecule's mass and its velocity.
The motion of the gas molecules is random in magnitude and direction; however, the average kinetic energy remains the same.
Recall from the kinetic molecular theory that the average translational kinetic energy per molecule depends only on the temperature.
Comparing the kinetic energy equations, rearranging the terms, and taking the square root on both sides relates the square root of the mean-square speed, also known as the root-mean-square or RMS speed.
With every collision, the velocity of individual gas particles change. Therefore, a collection of gas molecules has a slightly asymmetric velocity distribution curve known as the Maxwell-Boltzmann distribution. The peak of the curve corresponds to the most probable velocity, which is less than the RMS speed.
A plot of the velocity distribution for any gas at different temperatures displays an increase in the RMS speed and a broadening of the speed distribution at higher temperatures.
19.7:
Distribution of Molecular Speeds
The motion of molecules in a gas is random in magnitude and direction for individual molecules, but a gas of many molecules has a predictable distribution of molecular speeds. This predictable distribution of molecular speeds is known as the Maxwell-Boltzmann distribution. The distribution of molecular speeds in liquids is comparable to that of gases but not identical and can help to understand the phenomenon of the boiling and vapor pressure of a liquid. Consider that a molecule requires a speed equal to or more than at va to escape from the surface of a liquid into the adjacent vapor, as shown in Figure 1.
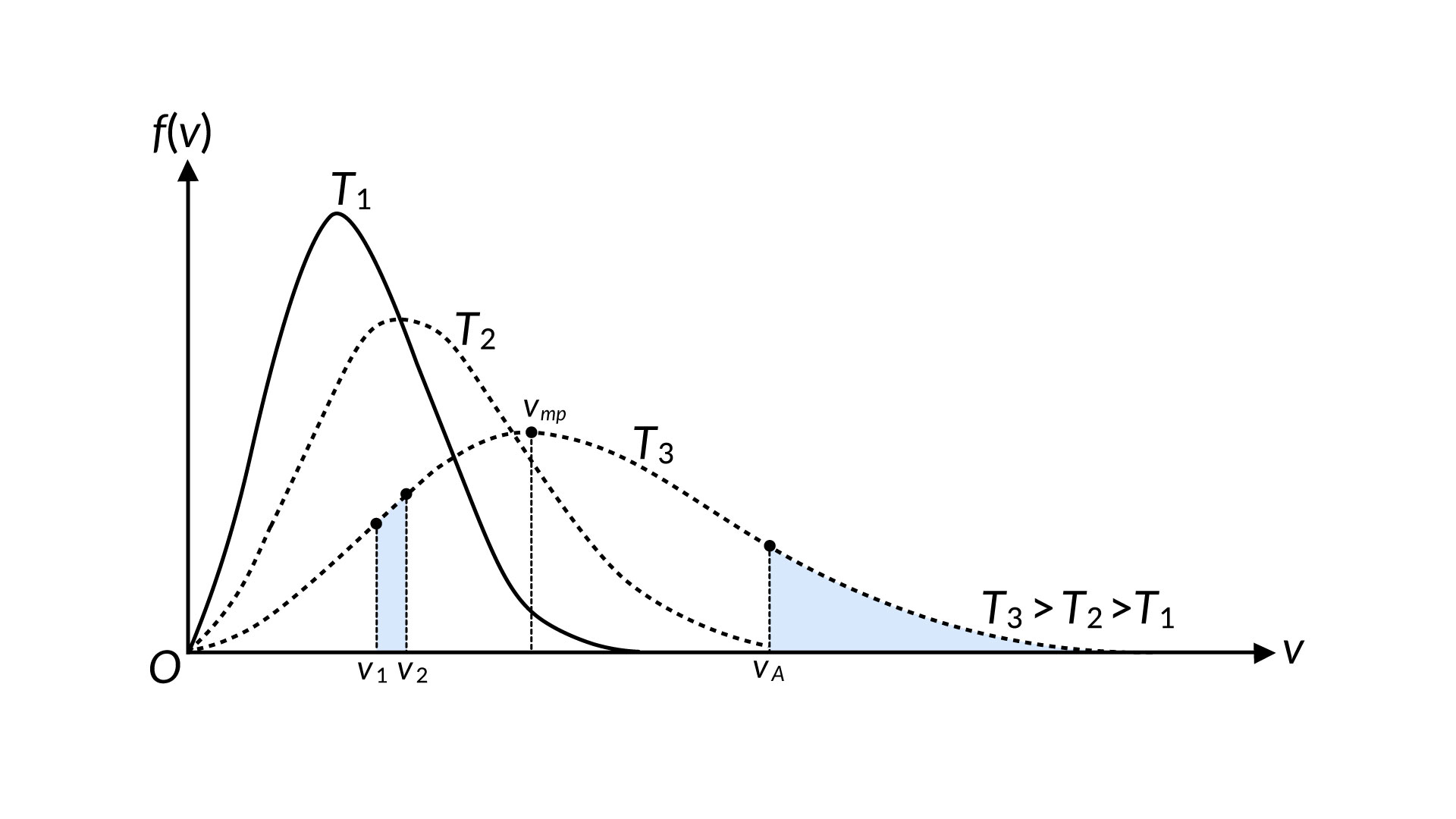
The number of similar molecules, represented by the area under the curve, increases swiftly with temperature. Thus, the rate at which molecules can escape is highly temperature-dependent. To counter this process, the molecules in the vapor phase collide inelastically with the surface and get trapped back in the liquid phase. The number of molecules that experience this situation per unit time is related to the vapor phase pressure. When these two processes proceed at the same rate, phase equilibrium is established between liquid and gas. So, if the molecular speed distributions are known for various temperatures, we can make a theoretical prediction of vapor pressure as a function of temperature. Rates of chemical reactions are often strongly temperature-dependent, and the reason for this is contained in the Maxwell-Boltzmann distribution.
Suggested Reading
- OpenStax. (2019). University Physics Vol. 2. [Web version], pages 94–95. Retrieved from https://openstax.org/books/university-physics-volume-2/pages/2-4-distribution-of-molecular-speeds
