3.14: Velocidad y posición mediante el Método Integral

Si se conoce la aceleración como función del tiempo, entonces las funciones de velocidad y posición se pueden derivar utilizando el cálculo integral. Para una aceleración constante, las ecuaciones integrales se refieren a las primeras y segundas ecuaciones cinemáticas para las funciones de velocidad y posición, respectivamente.

Consideremos un ejemplo para calcular la velocidad y posición a partir de la función de aceleración. Un barco a motor viaja a una velocidad constante de 5,0 m/s cuando comienza a desacelerar para llegar al muelle. Su aceleración es -1/4 * t m/s². Vamos a determinar el procedimiento para calcular la función de velocidad y posición del barco a motor.

Tomemos el tiempo, t = 0, cuando el barco comienza a desacelerar. Ahora, la función de velocidad se puede calcular utilizando la integral de la función de aceleración.

Utilizando la expresión de aceleración en la ecuación anterior, la velocidad como función del tiempo se calcula como:

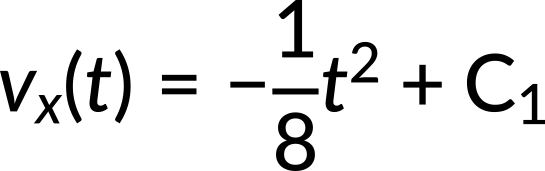
La constante de integración C₁ se calcula como 5 m/s utilizando el valor del tiempo inicial y la velocidad.

Por lo tanto, la velocidad como función del tiempo se reduce a:

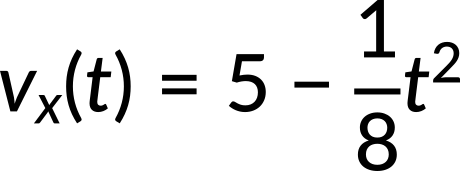
Al integrar la función de velocidad derivada con respecto al tiempo, se calcula la función de posición. La posición como función del tiempo es:

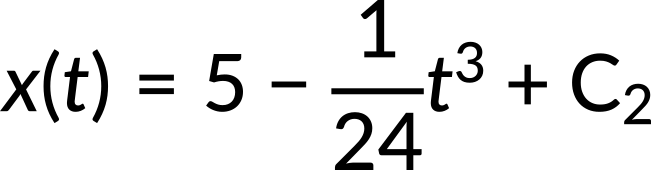
Una vez más, utilizando las condiciones iniciales, la constante de integración C₂ se calcula como cero.

Así, la posición como función del tiempo se reduce a:

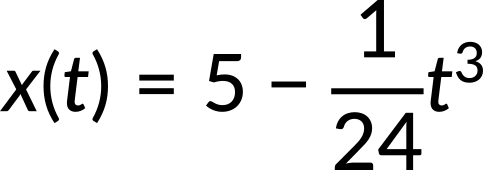
Este texto ha sido adaptado de Openstax, University Physics Volume 1, Section 3.6: Finding Velocity and Displacement from Acceleration.

La velocidad y la posición se pueden calcular si se conoce la aceleración en función del tiempo. La derivada temporal de la función de velocidad es la aceleración.

Entonces, tomando la integral en ambos lados de la ecuación, la velocidad se puede calcular en función del tiempo. La ecuación se puede reescribir para el caso de aceleración constante.

La constante de integración se puede calcular utilizando las condiciones iniciales. El valor de esta constante se sustituye en la expresión de la velocidad en función del tiempo para obtener la primera ecuación cinemática.

La derivada temporal de la función de posición es la función de velocidad. De nuevo, tomando la integral de ambos lados de la ecuación, se calcula la posición en función del tiempo.

Ahora, se sustituye la expresión de la función de velocidad y se integra la ecuación. Aplicando las condiciones iniciales, se deriva la constante de integración.

A continuación, el valor de esta constante se sustituye en la expresión de la posición en función del tiempo para obtener la segunda ecuación cinemática.