1.12:
Dimensional Analysis
The correct scientific measurement for any physical quantity is represented by an accurate numerical value expressed with the desired SI unit.
Dimensional analysis, also known as the factor label method, is a mathematical approach that is based on the principle that the units of quantities must be subjected to the same mathematical operations as their associated numbers.
Often, a single physical quantity can be expressed in different, but equivalent, units. For instance, the length of an object can be expressed as meters or centimeters, where 1 meter represents the same amount of length as 100 centimeters.
Dimensional analysis facilitates the conversion between such equivalent units through the use of the unit conversion factor.
The unit conversion factor is a ratio between two different units that measure the same physical quantity.
For instance, length in meters or centimeters can be interconverted, using conversion factors: 1 meter per 100 centimeters, and 100 centimeters per 1 meter.
The ratio of choice depends on the desired unit in the result. Thus, to determine the length in meters, the correct unit conversion factor is the ratio that cancels the units of centimeters and leaves meters.
Consider a 500 centimeter tall giraffe. To express its height in meters, both numbers and units, should be multiplied by the appropriate conversion factor. The numbers yield the product quantity, 5, and the units cancel out each other, except meters. Thus, the height of the giraffe is equal to 5 meters.
Sometimes a physical quantity that cannot be measured directly is calculated from other directly measured properties using equations and arithmetic operations. For instance, the density of an object can be calculated from its mass and volume.
Consider a plastic ball that has a mass of 12 g and a volume of 6 cm3. Its density can be determined by dividing its mass by its volume. The numbers and units are divided to yield the product quantity as 2 g/cm3.
Units, like numbers, are carried through all the steps of a calculation. In the end, the product quantity should have the desired units, and if not, this indicates errors in the use of conversion factors.
For example, the kinetic energy of a dog with a mass of 45 kg running at a speed of 11 m/s can be calculated using the mathematical equation, mass times velocity squared, divided by 2.
The speed of the dog is squared to 121 m2/s2 and multiplied by the mass of 45 kg.
Lastly, the total quantity is divided by 2 — yielding the kinetic energy of the dog as 2722.5 kg·m2/s2. Taking into account significant figures rounds the kinetic energy to 2700, or 2.7 × 103 kg·m2/s2.
The SI unit of energy is the joule, which is equal to one kilogram meter squared per second squared, or 2.7 × 103 joules.
1.12:
Dimensional Analysis
Dimensional analysis, also known as the factor label method, is a versatile approach for mathematical operations. The main principle behind this approach is: the units of quantities must be subjected to the same mathematical operations as their associated numbers. This method can be applied to computations ranging from simple unit conversions to more complex and multi-step calculations involving several different quantities and their units.
Conversion Factors and Dimensional Analysis
The unit conversion factor is a ratio of two equivalent quantities expressed with different measurement units. For example, 1.0936 yards and 1 meter measure the same length (by definition, 1.0936 yd = 1 m). Thus, to convert between these two equivalent units, a unit conversion factor is derived from the ratio
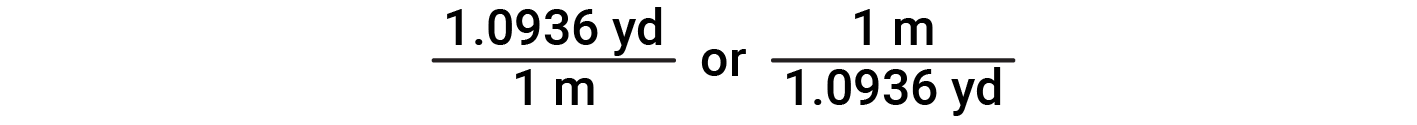
When a quantity (such as distance in yards) is multiplied or divided by an appropriate unit conversion factor, the quantity is converted to an equivalent value with different units (such as distance in meters). For example, a 25.0 m long lawn can be converted to yards by multiplying it with the appropriate conversion factor

Since this simple arithmetic involves quantities, the premise of dimensional analysis requires that we multiply both numbers and units. As the numbers of these two quantities are multiplied to yield the number of the product quantity, 27.3, similarly, the units are multiplied. Just as for numbers, a ratio of identical units is also numerically equal to one, and the unit product thus simplifies to yd. When identical units divide to yield a factor of 1, they are said to “cancel.”
Dimensional analysis may be used to confirm the proper application of unit conversion factors. Consider a 500 cm tall giraffe. To calculate the height in meters, the correct conversion factor must be used, which should cancel all other units except meters. The unit conversion factor for lengths in terms of meters and centimeters may be represented as

The correct unit conversion factor is the ratio that cancels the units of centimeters and provides an answer in meters.

Unit Conversion With Units Raised to a Power
While applying conversion factors for units raised to a power, both the number and the unit are raised to the same power. For example, to convert from yd2 to m2, the relationship between yd and m is used.
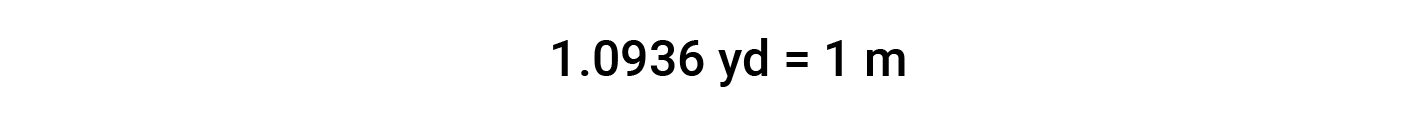
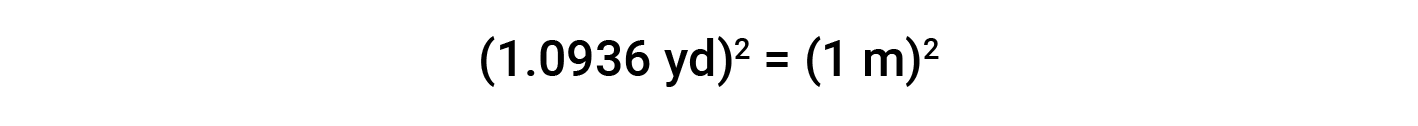
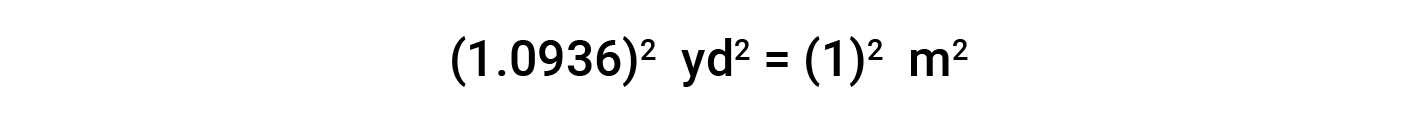
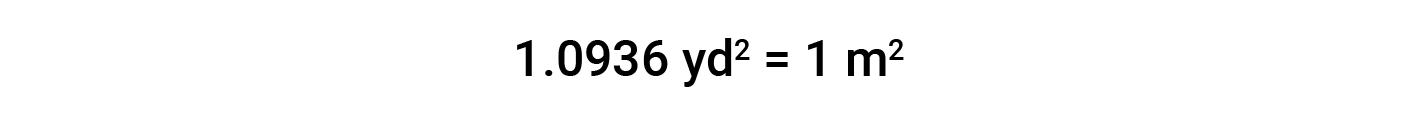
Beyond simple unit conversions, the factor-label method can be used to solve more complex problems involving computations. The basic approach is the same—all the factors involved in the calculation must be appropriately oriented to ensure that their units will appropriately cancel and/or combine to yield the desired unit in the result.
This text has been adapted from Openstax, Chemistry 2e, Section 1.6: Mathematical Treatment of Measurement Results.
